本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.INTRODUCTION
多人姿态估计的一些特点:1)每张图像可能包含未知数量的人,并且这些人可能在任何位置以任意比例出现;2)由于人与人之间的接触、遮挡等原因,使得关节点和人物的匹配变得困难;3)运行时间往往随着图像中人物数量的增多而增加,所以实时性也是一大挑战。
一种常见的方法是先用人物检测器把人检测出来,然后再对每个人进行姿态估计。这种top-down的方法可以直接利用已有的单人姿态估计技术,但其会受到人物检测器检测失败的影响。此外,这种方法的运行时间和人物数量成正比。相反,bottom-up的方法将运行时间与任务数量解耦。最初的一些bottom-up方法效率不高,推理一张图像需要几分钟的时间。
个人理解:bottom-up方法就是先检测出所有的关节点,然后将属于同一个人的关节点匹配到一起。
作者做了一个带标注的脚部数据集:foot dataset。
2.RELATED WORK
OpenPose是第一个用于身体、脚、手和面部关节点实时检测的开源库。
3.METHOD

Fig2是整体的pipeline。模型的输入为$w \times h$大小的彩色图像(Fig2(a)),然后将输入图像喂给一个前馈网络得到两个结果,一个是Fig2(b),另一个是Fig2(c)。先说Fig2(b),其得到的是一组heatmap(即文中所说的confidence map),用符号$\mathbf{S}$表示,每张heatmap对应一种关节点,比如Fig2(b)左所示的heatmap预测的是左肘(注意两个人的左肘都会被预测出来),Fig2(b)右所示的heatmap预测的则是两个人的左肩,假设一共有$J$个heatmap,那么有$\mathbf{S}=(\mathbf{S}_1, \mathbf{S}_2 , … , \mathbf{S}_J)$,且$\mathbf{S}_j \in \mathbb{R}^{w \times h}, j \in \{ 1, … , J \}$。然后再来说Fig2(c),其得到的是一组2D向量域,用符号$\mathbf{L}$表示,有$\mathbf{L} = (\mathbf{L}_1, \mathbf{L}_2 , … , \mathbf{L}_C)$,共有$C$个向量域(注意每个向量域内都有很多小向量,如Fig2(c)右所示),且有$\mathbf{L}_c \in \mathbb{R}^{w \times h \times 2}, c \in \{ 1, … , C \}$,其中$\mathbf{L}_c$表示躯干(limb),比如左肩$\to$左肘等。我们只把有对称分布的才称为limb,比如面部就不属于limb。然后,通过贪心推理(greedy inference)解析confidence maps和PAFs(Part Affinity Fields),如Fig2(d)所示,最终得到最后的结果(见Fig2(e))。

Fig1下左中一个个带颜色的小区域就是PAF(其实就是limb区域,比如右手肘到右手腕这一段肢体区域),不同颜色代表不同的方向。在PAF中的每个像素都对应一个向量,来表示limb的位置和方向,如Fig1下右所示。
3.1.Network Architecture
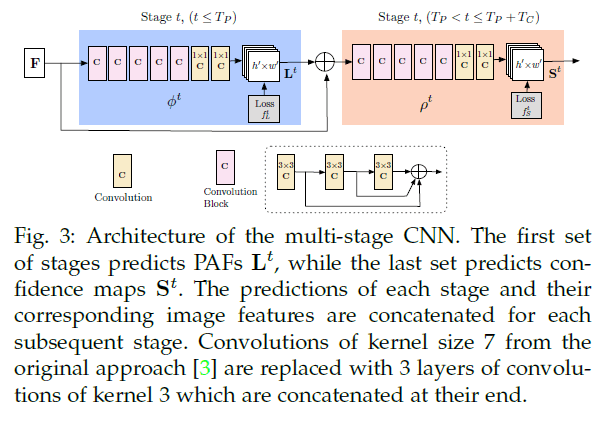
框架结构见Fig3,主要分为两个阶段:1)PAFs阶段生成$\mathbf{L}$;2)confidence map检测阶段生成$\mathbf{S}$。
3.2.Simultaneous Detection and Association
输入图像先经过一个CNN(这个CNN使用VGG-19的前10层进行初始化,并进行了fine-tune)得到$\mathbf{F}$。然后开始第一次迭代(即Stage 1),$\mathbf{F}$首先被喂入PAFs阶段,得到$\mathbf{L}^1 = \phi ^1 (\mathbf{F})$。然后继续进行PAFs阶段的第二次迭代(即Stage 2),第二次迭代的输入一部分来自上一次迭代的输出,另一部分来自图像特征$\mathbf{F}$,用公式可表示为:
\[\mathbf{L}^t = \phi ^t (\mathbf{F}, \mathbf{L}^{t-1}),\forall 2 \leq t \leq T_P \tag{1}\]PAFs阶段一共迭代$T_P$次。接下来进入confidence map检测阶段的迭代。
\[\mathbf{S}^{T_P} = \rho ^t (\mathbf{F}, \mathbf{L}^{T_P}), \forall t = T_P \tag{2}\] \[\mathbf{S}^t = \rho ^t (\mathbf{F}, \mathbf{L}^{T_P}, \mathbf{S}^{t-1}),\forall T_P < t \leq T_P + T_C \tag{3}\]confidence map检测阶段一共迭代$T_C$次,总迭代次数为$T=T_P+T_C$,有$t \in \{ 1, … , T \}$。
在OpenPose的初稿(论文“Z. Cao, T. Simon, S.-E. Wei, and Y. Sheikh, “Realtime multi-person 2d pose estimation using part affinity fields,” in CVPR, 2017.”)中,每次迭代我们对PAF和confidence map都进行了refine。这次修改之后,每次迭代的计算量减少了一半。并且我们发现精细的PAF改善了confidence map的结果,而相反的情况则不成立。
Fig4展示了PAF的refine过程。

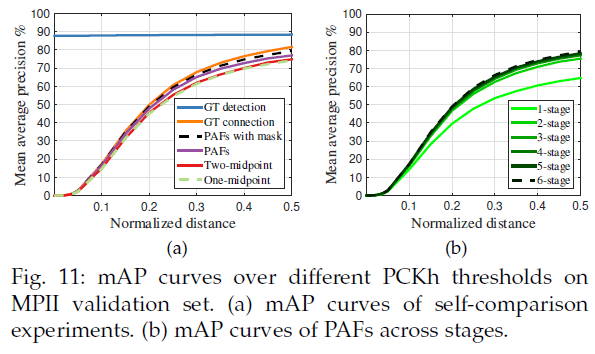
随着迭代次数的增加,PAF变得越来越精细,越来越准确。我们在PAFs阶段和confidence map检测阶段的末尾都添加了损失函数。
\[f_{\mathbf{L}}^{t_i} = \sum_{c=1}^C \sum_{\mathbf{p}} \mathbf{W}(\mathbf{p}) \cdot \parallel \mathbf{L}_c^{t_i}(\mathbf{p}) - \mathbf{L}_c^* (\mathbf{p}) \parallel_2^2 \tag{4}\] \[f_{\mathbf{S}}^{t_k} = \sum_{j=1}^J \sum_{\mathbf{p}} \mathbf{W} (\mathbf{p}) \cdot \parallel \mathbf{S}_j^{t_k} (\mathbf{p}) - \mathbf{S}_j^* (\mathbf{p}) \parallel _2^2 \tag{5}\]其中,$\mathbf{L}_c^{*}$是PAF的GT,$\mathbf{S}_j^{*}$是confidence map的GT,$\mathbf{W}$是一个二值mask,当像素$\mathbf{p}$没有标注时,有$\mathbf{W}(\mathbf{p})=0$。总的损失函数表示为:
\[f = \sum_{t=1}^{T_P} f_{\mathbf{L}}^t + \sum_{t= T_P + 1}^{T_P + T_C} f_{\mathbf{S}}^t \tag{6}\]3.3.Confidence Maps for Part Detection
为了在训练中评估式(6)的$f_{\mathbf{S}}$,我们根据标注的2D关节点生成了groundtruth confidence maps $\mathbf{S}^{*}$。 先考虑图像中只有一个人的情况,对于每个人$k$的第$j$个关节点,$x_{j,k} \in \mathbb{R}^2$是该点的真实像素位置,然后我们采用常见的高斯分布来生成heatmap:
\[\mathbf{S}_{j,k}^* (\mathbf{p}) = \text{exp} \left( -\frac{\parallel \mathbf{p} - x_{j,k} \parallel _2^2}{\sigma ^2} \right) \tag{7}\]那如果是多人的情况,则会取一个最大值:
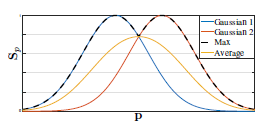
\[\mathbf{S}_j^* (\mathbf{p}) = \max _k \mathbf{S}_{j,k}^* (\mathbf{p}) \tag{8}\]如下图所示,如果我们使用取平均而不是取最大值的方式,则会影响峰值附近的精度。在预测confidence map时使用了NMS。
3.4.Part Affinity Fields for Part Association
有了检测的关节点(如Fig5(a))之后,我们该如何将这些关节点匹配起来呢?我们需要计算每一对limb关节点(见Fig5(a)灰色线)的置信度,以判断它们是否属于同一个人。一个可行的方法是再额外检测出每一对limb关节点的中点(见Fig5(b)黄色点),以此来进一步判断每对limb关节点的归属。但这种方法会导致如Fig5(b)绿色线那样的错误。这种错误源自该方法的两个限制:1)只考虑了limb的位置,而没有考虑其方向;2)将limb的支持区域减少到了单个点。

PAF则解决了这些限制。PAF保留了limb支持区域的位置和方向信息(如Fig5(c)所示)。每一个PAF都是一个limb的2D向量域,如Fig1下右所示。2D向量域中的每个小向量都从limb的一端指向另一端。
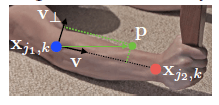
考虑如下图所示的limb。用$x_{j_1,k},x_{j_2,k}$表示关节点的GT位置,$k$表示图像中的第$k$个人,$j_1,j_2$为limb $c$所连接的两个关节点。如果点$\mathbf{p}$位于limb区域内,则该点的GT 2D向量表示为$\mathbf{L}_{c,k}^* (\mathbf{p})$,其是一个单位向量,方向从$j_1$指向$j_2$。而在非limb区域的点都设为零向量。
为了在训练中评估式(6)的$f_{\mathbf{L}}$,我们定义PAF的GT如下:
\[\mathbf{L}_{c,k}^* (\mathbf{p}) = \begin{cases} \mathbf{v}, & \text{if p on limb c,k} \\ 0, & \text{otherwise} \end{cases} \tag{9}\]其中,$\mathbf{v} = (x_{j_2,k} – x_{j_1,k}) / \parallel x_{j_2,k} – x_{j_1,k} \parallel_2$是一个单位向量。那么如何判断点$\mathbf{p}$是否落在了limb c,k上呢?如果点$\mathbf{p}$落在limb c,k区域内,则应满足下式:
\[0 \leq \mathbf{v} \cdot (\mathbf{p} - x_{j_1,k}) \leq l_{c,k} \ \text{and} \ \lvert \mathbf{v}_{\perp} \cdot (\mathbf{p} - x_{j_1,k}) \rvert \leq \sigma _l\]其中,$\sigma_l$是limb的宽度(单位是像素),宽度是沿着$\mathbf{v}_{\perp}$方向的,而$\mathbf{v}_{\perp}$是和$\mathbf{v}$垂直的。$l_{c,k}$是limb的长度(单位是像素),长度是沿着$\mathbf{v}$方向的。
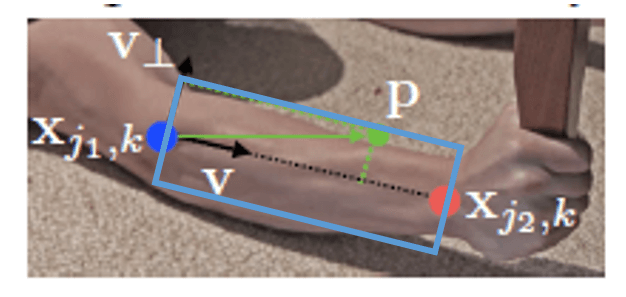
简单解释下上式,$\mathbf{p}-x_{j_1,k}$就是上图绿色向量(我们暂记为$\mathbf{a}$),其和单位向量$\mathbf{v}$进行点积:$\mathbf{v} \cdot \mathbf{a} = \lvert \mathbf{v} \rvert \lvert \mathbf{a} \rvert \cos <\mathbf{v},\mathbf{a}> = \lvert \mathbf{a} \rvert \cos <\mathbf{v},\mathbf{a}>$,就相当于得到了绿色向量在$\mathbf{v}$方向上的投影长度,我们要限制这个长度在$[0,l_{c,k}]$。在$\mathbf{v}_{\perp}$方向对宽度的限制同理。简单来说,其实每个limb区域就是一个旋转的矩形框(如下图蓝框所示),落在矩形框内的点即被视为落在了limb上。
考虑图像中的所有人,PAF的GT可定义为:
\[\mathbf{L}_c^* (\mathbf{p}) = \frac{1}{n_c (\mathbf{p})} \sum_k \mathbf{L}_{c,k}^* (\mathbf{p}) \tag{10}\]$n_c(\mathbf{p})$为所有的$k$个人在点$\mathbf{p}$处非零向量的个数。
个人理解:如果$k$个人在点$\mathbf{p}$处的向量的方向都不同,那这么算可能会存在问题,因为一个点就只能被综合为一个方向。
在预测阶段,假设图像有两个人,heatmap1预测得到两个左肘位置(假设记为左肘1和左肘2),heatmap2预测得到两个左腕位置(假设记为左腕1和左腕2),那么我们该如何判断左肘1应该是和左腕1相连还是左腕2相连呢?因此我们需要一个关联置信度,来判断左肘1-左腕1相连更合适,还是左肘1-左腕2相连更合适。假设我们把左肘1记为$\mathbf{d}_{j_1}$,左腕1记为$\mathbf{d}_{j_2}$,那左肘1和左腕1相连得到的limb的PAF记为$\mathbf{L}_c$,那么左肘1-左腕1的关联置信度可用下式计算:
\[E = \int_{u=0}^{u=1} \mathbf{L}_c (\mathbf{p}(u)) \cdot \frac{\mathbf{d}_{j_2} - \mathbf{d}_{j_1}}{\parallel \mathbf{d}_{j_2} - \mathbf{d}_{j_1} \parallel _2} du \tag{11}\]其中,$\mathbf{p}(u)$是$\mathbf{d}_{j_1}$和$\mathbf{d}_{j_2}$之间的插值:
\[\mathbf{p}(u) = (1-u) \mathbf{d}_{j_1} + u \mathbf{d}_{j_2} \tag{12}\]因为如果在计算关联置信度时考虑到limb区域内的所有点,会使得计算量很大,所以我们只考虑$\mathbf{d}_{j_1}$和$\mathbf{d}_{j_2}$所连线段上的点(即$\mathbf{p}(u)$)。因为线段上可以取无数多个点,所以在式(11)中用到了积分。而在实际实现时,我们会对$u$进行均匀间隔采样来近似积分。如果线段上的点对应的2D向量越接近沿着线段方向,那么算出来的关联置信度(即$E$)就越大。

如上图所示,假设我们对$u$均匀采样了4个值,即在线段上取4个点,每个点对应的2D向量用红色箭头表示,左肘1-左腕2的关联置信度要高于左肘1-左腕1。
3.5.Multi-Person Parsing using PAFs
假设一张图里有3个人,那么我们预测可以得到3个左肘和3个左腕。如果不考虑同一类型关节点的连接,我们可以得到如下所有可能的连接方式:
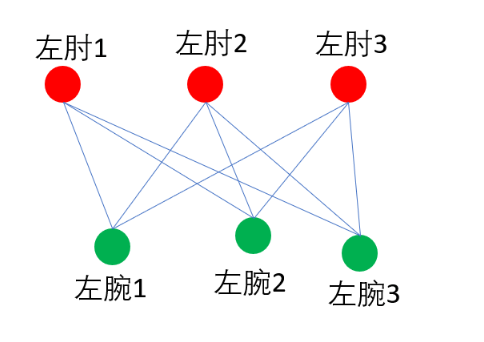
这是一个典型的二分图最大匹配问题,我们可以用匈牙利算法来得到最大匹配(在匹配算法之前,我们可以通过一些限制条件来删掉一些边,比如把低于关联置信度阈值的连接删除),因为匈牙利算法的解不是唯一的,所以我们能得到多个最大匹配方案。比如下面是两种不同的最大匹配方案,我们该如何判断哪种匹配方案更好呢?
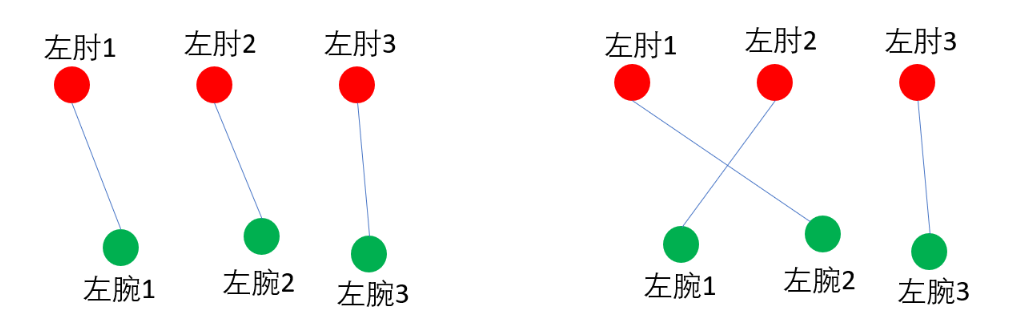
这就需要用到我们在第3.4部分介绍的关联置信度了,以上图左为例,该匹配方案的关联置信度可定义为:E(左肘1-左腕1)+E(左肘2-左腕2)+E(左肘3-左腕3)。我们的目标就是找到关联置信度最高的匹配方案。以上便是自己用通俗语言对本部分的介绍,接下来按照论文的思路,我们再进一步的了解下这部分。
首先在检测到的confidence map上使用NMS得到一系列关节点。由于图像中可能会存在多个人或者检测出现了假阳,同一类型的关节点会有多个候选点(见Fig6(b))。这些候选点能够定义出非常多可能的limb。对于这些limb,我们都可以用式(11)计算其关联置信度。但这种K维匹配属于是NP-Hard的问题(见Fig6(c),可简单理解为几乎无法在可接受时间内对K维匹配进行求解)。因此我们提出一种贪心松弛(greedy relaxation)的策略,其可以一直获得高质量的匹配。
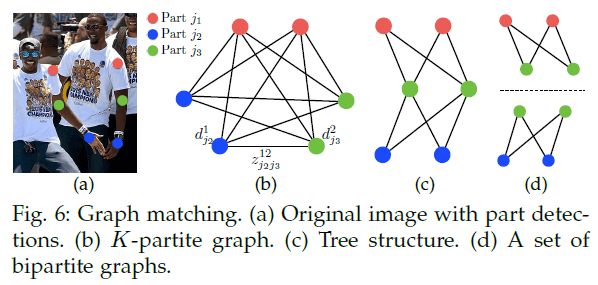
首先,我们定义一组关节点:$\mathcal{D}_{\mathcal{J}} = \{ \mathbf{d}_j^m \ : \ \text{for} \ j \in \{ 1 … J \}, \ m \in \{ 1 … N_j \} \}$,其中,$j$表示关节点的类型,$N_j$表示类型为$j$的关节点的候选点数量,$\mathbf{d}_j^m \in \mathbb{R}^2$表示类型为$j$的关节点的第$m$个候选点。我们用$z_{j_1 j_2}^{mn} \in \{ 0,1 \}$表示两个不同类型的关节点候选点$\mathbf{d}_{j_1}^m$和$\mathbf{d}_{j_2}^n$是否相连,$\mathcal{Z} = \{ z_{j_1 j_2}^{mn} \ : \ \text{for} \ j_1,j_2 \in \{ 1 … J \}, \ m\in \{ 1 … N_{j_1} \}, \ n \in \{ 1…N_{j_2} \} \}$,目标就是寻找一组最优连接。
为了避免K维匹配的NP难问题,我们一次只考虑一个limb,比如只考虑第$c$个limb,其连接的两个关节点为$j_1$和$j_2$(比如脖子和右髋),这样就将K维匹配转化成了多个最大权重的二分图匹配问题。二分图的两个点集分别是$\mathcal{D}_{j_1},\mathcal{D}_{j_2}$,边是所有可能的连接。边的权重是通过式(11)计算得到的关联置信度。同一个点不能被两条边共享。我们的目标就是寻找权重最大的匹配方案:
\[\begin{align} &\max_{\mathcal{Z}_c} E_c = \max_{\mathcal{Z}_c} \sum_{m \in \mathcal{D}_{j_1}} \sum_{n \in \mathcal{D}_{j_2}} E_{mn} \cdot z_{j_1 j_2}^{mn} \quad (13) \\ & \begin{array}{r@{\quad}r@{}l@{\quad}l} s.t.& \forall m \in \mathcal{D}_{j_1}, \ \sum_{n \in \mathcal{D}_{j_2}} z_{j_1 j_2}^{mn} \leq 1 \quad (14) \\& \forall n \in \mathcal{D}_{j_2}, \ \sum_{m \in \mathcal{D}_{j_1}} z_{j_1 j_2}^{mn} \leq 1 \quad (15) \\ \end{array} \end{align}\]$E_c$是针对第$c$个limb的某一匹配方案的总权重,$\mathcal{Z}_c$是针对第$c$个limb的某一匹配方案,$E_{mn}$是$\mathbf{d}_{j_1}^m$和$\mathbf{d}_{j_2}^n$的关联置信度(计算见式(11))。式(14)和式(15)用于限制两条边不能共用一个点,即两个同一类型的limb(比如两个左前臂)不能使用同一个关节点。我们可以使用匈牙利算法来获得最优匹配。
式(15)只考虑第$c$个limb,如果考虑全身所有的limb,则优化目标为:
\[\max_{\mathcal{Z}} E = \sum_{c=1}^C \max_{\mathcal{Z}_c} E_c \tag{16}\]只要我们把所有检测到且有共同关节点的limb组合起来,便可得到一个人的全身关节点。
我们现在的模型中包含了很多冗余的PAF连接(比如耳朵-肩膀、手腕-肩膀等)。这些冗余的连接提高了在拥挤图像中的精度,如Fig7所示。为了处理这些冗余连接,我们对多人解析算法进行了微调。在初始方法中,我们从一个limb开始,依次连接有共同关节点的其他limb,而微调之后的方法是,将所有limb按照PAF分数(即关联置信度)进行降序排列,从最高PAF分数的limb开始逐个连接。如果有一个连接试图连接已经分配给了两个不同人的关节点,那么这个连接会被忽略。

4.OPENPOSE
为了帮助其他的研究工作,我们开源了OpenPose,是第一个实时、多人系统,用于检测人物面部、脚部、手部和身体的关节点(一共135个关节点)。例子见Fig8。

4.1.System
现在可用的一些2D姿态估计库,比如Mask R-CNN或Alpha-Pose,都需要用户自己实现大部分的pipeline,比如他们自己的frame reader(比如视频、图像或相机流)以及自己去可视化结果。并且这些方法没有集成对脸部关节点的检测。OpenPose解决了这些问题。OpenPose可以在不同平台上运行,包括Ubuntu、Windows、Mac OSX和嵌入式系统(比如Nvidia Tegra TX2)。OpenPose还支持不同的硬件,比如CUDA GPUs、OpenCL GPUs以及CPU。用户的输入可以选择图像、视频、webcam和IP camera streaming。用户也可以选择是否显示结果并保存它们,可以enable或disable每个检测器(身体、脚、面部和手部),还支持像素坐标归一化,还能指定使用几块GPU,还可以选择是否跳帧来获得更快的处理等等。
OpenPose包括3个不同的block:1)body+foot检测;2)hand检测;3)face检测。其中,core block是body+foot检测器(见第4.2部分)。它可以使用在COCO和MPII上训练的body-only的模型。基于body-only检测模型得到的耳朵、眼睛、鼻子、脖子等关节点的位置,我们可以粗略得到facial bounding box proposals。类似的,通过胳膊关节点我们可以得到hand bounding box proposals。这里采用了第1部分提到的top-down的方式。手部关节点的检测算法见论文“T. Simon, H. Joo, I. Matthews, and Y. Sheikh, “Hand keypoint detection in single images using Multiview bootstrapping,” in CVPR, 2017.”,面部关节点检测算法的训练方式和手相同。OpenPose库还包括3D keypoint pose detection。
在保证高质量结果的同时,OpenPose的推理速度优于所有的SOTA方法。在Nvidia GTX 1080 Ti上能达到22 FPS(见第5.3部分)。
4.2.Extended Foot Keypoint Detection
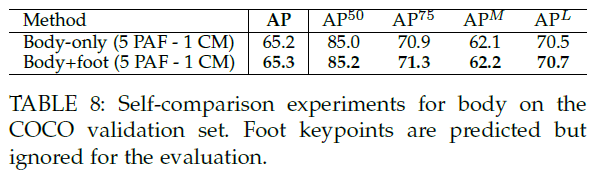
现在的人体姿态数据集只包含有限的身体部位。MPII数据集标注了脚踝、膝盖、髋、肩膀、手肘、手腕、脖子、躯干和头顶,COCO还多包含了一些面部的关节点。对于这两个数据集,脚部标注就只有脚踝。然而,对于一些应用,比如3D人物重建,则需要脚部更多的关节点,比如大脚趾和脚跟。基于此,我们使用Clickworker平台对COCO数据集中的一部分数据进行了脚部关节点的标注。有14K个标注实例来自COCO训练集,有545个标注实例来自COCO验证集。一共标注了6个脚部关节点(见Fig9(a))。
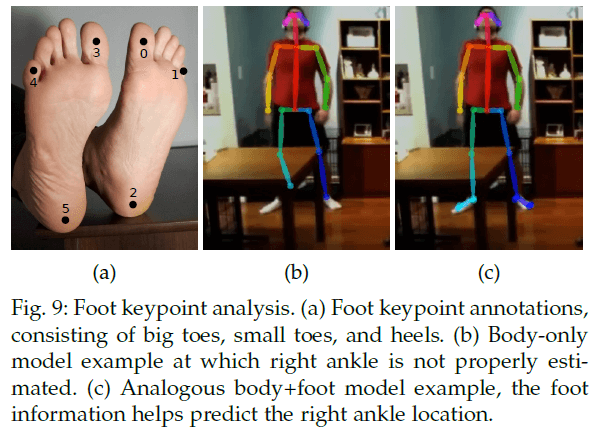
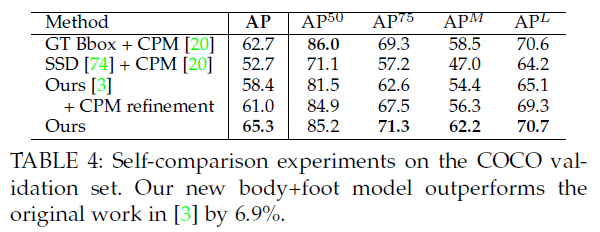
使用我们的数据集,我们训练了一个脚部关节点检测算法。最简单的想法是,我们基于身体关节点检测器生成脚部bbox proposals,然后再训练一个脚部检测器。但这种top-down结构存在一些特有问题(见第1部分)。因此,我们在先前提到的身体关节点检测器的框架中直接加入了对脚部关节点的预测。3种数据集(COCO、MPII、COCO+foot)的关节点标注见Fig10。即使上半身被遮挡或不在图像中,我们的body+foot模型依然可以检测到双腿和脚部。并且我们发现,脚部关节点潜在提升了身体关节点的检测精度,尤其是腿部关节点,比如脚踝位置,例子见Fig9(b)和Fig9(c)。

5.DATASETS AND EVALUATIONS
我们在多人姿态估计的3个benchmark上进行了评估:1)MPII数据集,包含3844个training groups和1758个testing groups,标注了14个身体关节点;2)COCO数据集,标注了17个关节点(12个身体关节点+5个面部关节点);3)我们自己的脚部数据集。我们的方法在COCO 2016 keypoints challenge中取得了第一名,在MPII上也大大超过了其他SOTA方法。
5.1.Results on the MPII Multi-Person Dataset
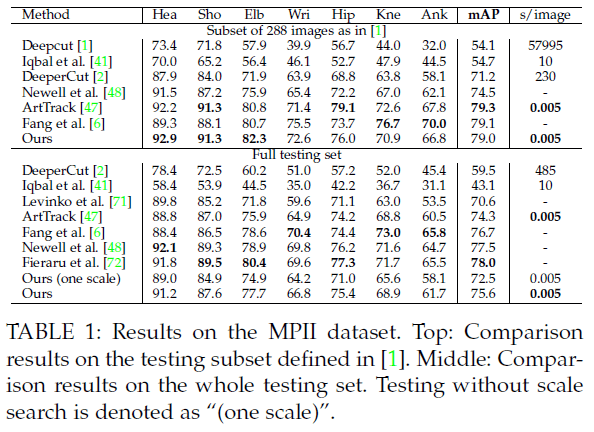
表1中”Ours(one scale)”表示没有使用scale search,”Ours”表示使用了3种scale search($\times 0.7,\times 1,\times 1.3$)。

表2是Fig6中不同匹配策略的测试结果。我们从原始的MPII训练集中选取了343张图像作为我们的自定义验证集。Fig6(d)是本文提出的方法。这几种策略得到了相似的结果,说明使用最小边(minimal edges)就足够了。我们训练我们的最终模型,只学习最小边以充分利用network capacity,见Fig. 6d (sep)(这部分没太明白)。
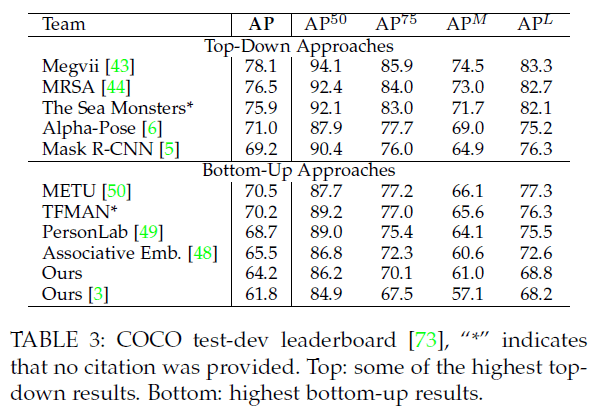
5.2.Results on the COCO Keypoints Challenge
COCO训练集包括超过100K个人物实例,共计超1百万个标注关节点。测试集包含”test-challenge”和”test-dev”子集,每个子集约20K张图像。
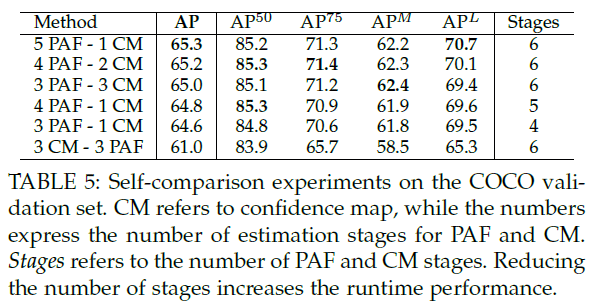
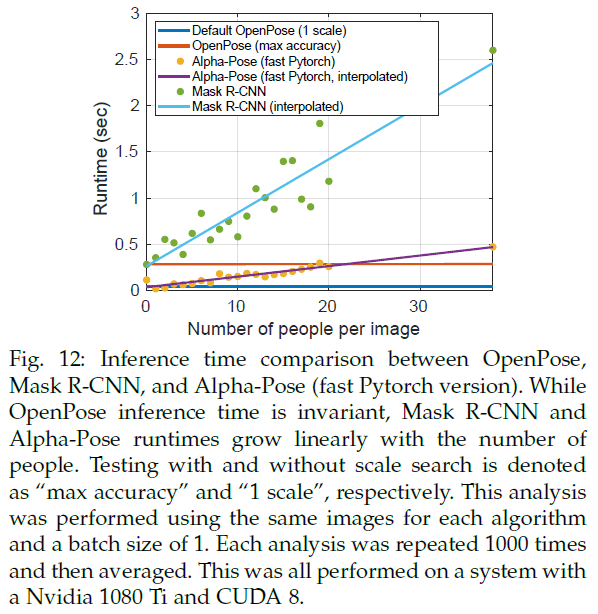
5.3.Inference Runtime Analysis
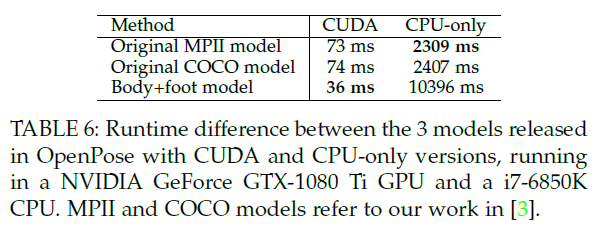
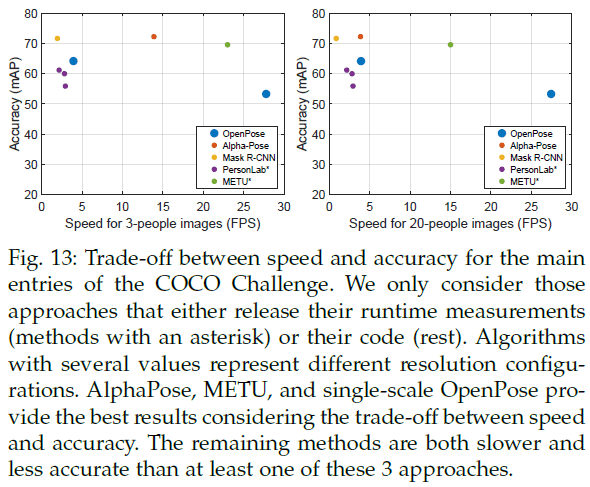
5.4.Trade-off between Speed and Accuracy
5.5.Results on the Foot Keypoint Dataset

5.6.Vehicle Pose Estimation
OpenPose还可以用于车辆关键点的检测。


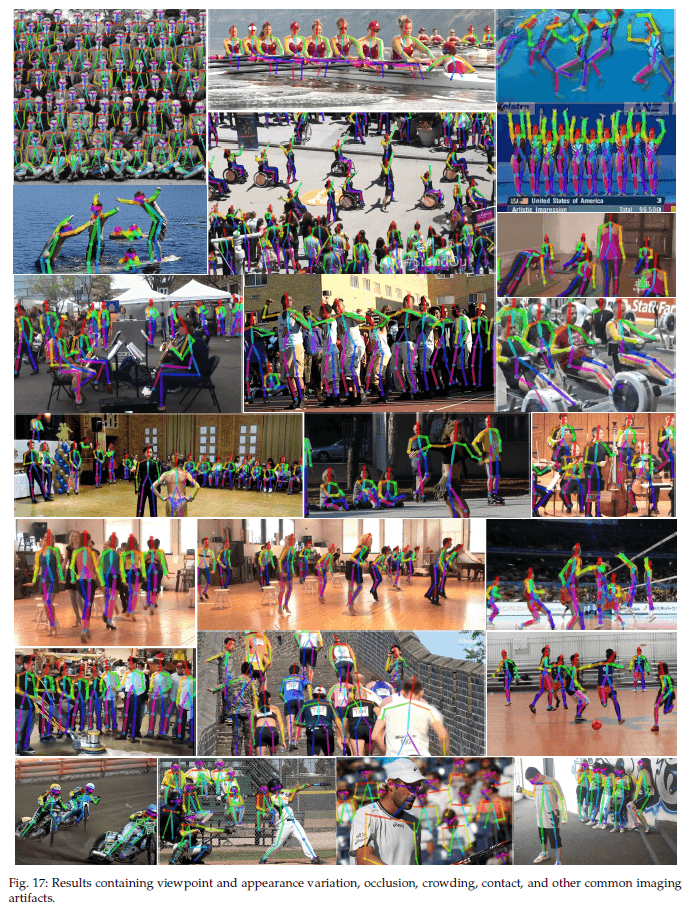
5.7.Failure Case Analysis

6.CONCLUSION
OpenPose已经被集成到OpenCV里了。
7.原文链接
👽OpenPose:Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields