本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.INTRODUCTION
对于大多数常规相机(无论是窄角镜头还是广角镜头)来说,针孔相机模型(pinhole camera model)都是一个相当合理的近似。但它并不适用于鱼眼镜头的相机,鱼眼镜头可以覆盖相机前方整个半球视野,视角大约为180度。此外,通过透视投影(perspective projection)将半球视野投影到有限的图像平面上是不可能的。
在本文中,我们专注于对真实相机的精确几何建模。我们提出了一种新的鱼眼镜头校正方法,该方法要求相机观察一个平面校正图案。该校正方法基于一种通用相机模型,且该模型适用于不同类型的全向相机(omnidirectional camera,即360-degree camera,亦称全景相机)以及常规相机。
2.GENERIC CAMERA MODEL
由于透视投影模型不适合鱼眼镜头,我们使用了一个更灵活的径向对称投影模型(radially symmetric projection model)。
个人注解:径向就是沿着半径的方向,切向就是垂直于半径的方向。
2.A.Radially Symmetric Model

Fig1(b)中,$x-y$是图像坐标系,$X_c-Y_c-Z_c$是相机坐标系。
如Fig1所示,针孔相机的透视投影(个人注解:针孔相机模型中,光线是按直线传播的)可用下式表示:
\[r = f \tan \theta \quad (\text{i. perspective projection}) \tag{1}\]其中,$\theta$是主轴(principal axis)和入射光线的夹角,$r$是像点(image point)和主点(principal point)之间的距离,$f$是焦距(focal length)。而不同的鱼眼镜头有不同的投影函数,常见的有:
\[r = 2 f \tan (\theta / 2) \quad (\text{ii. stereographic projection}) \tag{2}\] \[r = f \theta \quad (\text{iii. equidistance projection}) \tag{3}\] \[r = 2 f \sin (\theta / 2) \quad (\text{iv. equisolid angle projection}) \tag{4}\] \[r = f \sin (\theta) \quad (\text{v. orthogonal projection}) \tag{5}\]最常用的是equidistance projection,即式(3)。几种不同投影方式的区别见Fig1(a),针孔相机和鱼眼相机的区别见Fig1(b)。
但是,真实的镜头并不完全遵循上述设计的投影模型。为了适用不同类型镜头的模型,我们考虑以下更通用的投影:
\[r(\theta) = k_1 \theta + k_2 \theta^3 + k_3 \theta^5 + k_4 \theta^7 + k_5 \theta^9 + \cdots \tag{6}\]为了不失一般性,偶次幂被省略。我们发现使用前五项就可以很好的近似不同的投影曲线。因此,我们相机模型的径向对称部分包含5个参数:$k_1,k_2,k_3,k_4,k_5$。
我们用$\mathcal{F}$表示入射光线到归一化图像坐标的转换:
\[\begin{pmatrix} x \\ y \end{pmatrix} = r(\theta) \begin{pmatrix} \cos \varphi \\ \sin \varphi \end{pmatrix} = \mathcal{F} (\Phi) \tag{7}\]其中,$r(\theta)$使用式(6)中的前5项,$\Phi = (\theta, \varphi)^{\top}$是入射光线的方向。
个人注解:式(7)相当于相机坐标系到图像坐标系的转换。$P$确定了之后,$\theta$和$\varphi$就也确定了。
2.B.Full Model
第2.A部分是没有考虑畸变时的情况。我们定义径向方向的畸变为:
\[\Delta _r (\theta, \varphi) = (l_1\theta+l_2\theta^3+l_3\theta^5)(i_1\cos \varphi + i_2 \sin \varphi + i_3 \cos 2\varphi + i_4 \sin 2\varphi) \tag{8}\]定义切向方向的畸变为:
\[\Delta_t(\theta,\varphi)=(m_1\theta+m_2\theta^3+m_3\theta^5)(j_1\cos \varphi+j_2\sin \varphi + j_3\cos 2\varphi + j_4\sin 2\varphi) \tag{9}\]式(8)和式(9)各有7个参数。
将径向畸变和切向畸变考虑进式(7),得到畸变后的点坐标$\mathbf{x}_d = (x_d,y_d)^{\top}$为:
\[\mathbf{x}_d = r(\theta) \mathbf{u}_r(\varphi) + \Delta_r(\theta,\varphi)\mathbf{u}_r(\varphi) + \Delta_t(\theta,\varphi)\mathbf{u}_{\varphi}(\varphi) \tag{10}\]个人注解:式(10)也很好理解,从没有畸变的点开始,沿着径向方向,先做径向畸变,再沿切向方向做切向畸变。式(10)相当于是在图像坐标系下的畸变过程。
其中,$\mathbf{u}_r(\varphi)$和$\mathbf{u}_{\varphi}(\varphi)$分别是径向和切向的单位向量。图像坐标系到像素坐标系的转换:
\[\begin{pmatrix} u \\ v \end{pmatrix} = \begin{bmatrix} m_u & 0 \\ 0 & m_v \end{bmatrix} \begin{pmatrix} x_d \\ y_d \end{pmatrix} + \begin{pmatrix} u_0 \\ v_0 \end{pmatrix} = \mathcal{A}(\mathbf{x}_d) \tag{11}\]个人注解:$u-v$是像素坐标系。
其中,$(u_0,v_0)^{\top}$是主点,$m_u$是水平方向一个单位距离包含的像素点数目,$m_v$是竖直方向一个单位距离包含的像素点数目。
结合式(10)和式(11),我们可以得到前向相机模型(forward camera model):
\[\mathbf{m} = \mathcal{P}_c(\Phi) \tag{12}\]个人注解:式(12)就是从相机坐标系到像素坐标系的转换(带畸变),也就是相机内参。
其中,$\mathbf{m}=(u,v)^{\top}$。完整的相机模型一共有23个参数(5个投影参数+14个畸变参数+$m_u,m_v,u_0,v_0$),我们用$\mathbf{p}_{23}$表示这23个参数。
这个模型非常的灵活,可以被简化使用。如果不考虑畸变,那么相机模型的参数只有9个。在后续的实验中,我们还测试了只有6个参数的相机模型(去掉了$k_3,k_4,k_5$)。
2.C.Backward Model
个人注解:作者这里的前向相机模型指的是从相机坐标系到像素坐标系的转换。反向相机模型指的是从像素坐标系到相机坐标系的转换。
反向相机模型(backward camera model):
\[\Phi = \mathcal{P}_c^{-1}(\mathbf{m}) \tag{13}\]我们将$\mathcal{P}_c$表示为:
\[\mathcal{P}_c = \mathcal{A} \circ \mathcal{D} \circ \mathcal{F}\]其中,$\mathcal{F}$就是式(7),$\mathcal{D}$就相当于式(10),$\mathcal{A}$就是式(11)。
反向变换表示为:
\[\mathcal{P}_c^{-1} = \mathcal{F}^{-1} \circ \mathcal{D}^{-1} \circ \mathcal{A}^{-1}\]其中,$\mathcal{F}^{-1}$和$\mathcal{A}^{-1}$的计算很简单。$\mathcal{D}^{-1}$的计算比较困难。
给定点$\mathbf{x}_d$,求$\mathbf{x} = \mathcal{D}^{-1}(\mathbf{x}_d)$的过程可视为求式子$\mathbf{x} = \mathbf{x}_d - \mathbf{s}$中$\mathbf{s}$的过程,其中:
\[\mathbf{s} = \mathcal{S}(\Phi) = \Delta_r(\theta,\varphi)\mathbf{u}_r(\varphi)+\Delta_t(\theta,\varphi)\mathbf{u}_{\varphi}(\varphi) \tag{14}\]我们定义下式:
\[\mathcal{S}(\Phi) \equiv (\mathcal{S} \circ \mathcal{F}^{-1})(\mathbf{x})\]个人注解:$\mathcal{S}$是关于$\Phi$的函数,我们将其改为关于$\mathbf{x}$的函数。$\mathbf{x}$先通过$\mathcal{F}^{-1}$得到$\Phi$(即式(7)的反向计算),然后再将$\Phi$喂给$\mathcal{S}$。
我们结合上式,对式(14)在$\mathbf{x}_d$处进行一阶泰勒展开:
\[\begin{align} \mathbf{s} &\simeq (\mathcal{S}\circ \mathcal{F}^{-1})(\mathbf{x}_d) + \frac{\partial(\mathcal{S} \circ \mathcal{F}^{-1})}{\partial \mathbf{x}} (\mathbf{x}_d) (\mathbf{x}-\mathbf{x}_d) \\&= \mathcal{S}(\Phi_d) - \frac{\partial \mathcal{S}}{\partial \Phi} \left( \frac{\partial \mathcal{F}}{\partial \Phi} (\Phi_d) \right)^{-1} \mathbf{s} \end{align}\]其中,$\Phi_d = \mathcal{F}^{-1}(\mathbf{x}_d)$可被计算得到。因此,我们可以通过下式计算$\mathbf{s}$:
\[\mathbf{s} \simeq \left( I + \frac{\partial \mathcal{S}}{\partial \Phi}(\Phi_d) \left( \frac{\partial \mathcal{F}}{\partial \Phi}(\Phi_d) \right)^{-1} \right)^{-1} \mathcal{S}(\Phi_d) \tag{15}\]雅可比矩阵(Jacobians)$\frac{\partial \mathcal{S}}{\partial \Phi}$和$\frac{\partial \mathcal{F}}{\partial \Phi}$可通过式(14)和式(7)计算得到。所以,最终:
\[\mathcal{D}^{-1}(\mathbf{x}_d) \simeq \mathbf{x}_d - \left( I + \left( \frac{\partial \mathcal{S}}{\partial \Phi} \circ \mathcal{F}^{-1} \right) (\mathbf{x}_d) \left( \left( \frac{\partial \mathcal{F}}{\partial \Phi} \circ \mathcal{F}^{-1} \right) (\mathbf{x}_d) \right)^{-1} \right)^{-1} (\mathcal{S}\circ \mathcal{F}^{-1})(\mathbf{x}_d) \tag{16}\]对于非对称畸变函数$\mathcal{D}$的一阶近似在实际中是可行的,因为反向模型误差通常比前向模型的校准精度小几个数量级。
3.JUSTIFICATION OF THE PROJECTION MODEL
传统的相机校正方法是以透视投影模型作为起点,然后辅以畸变项。然而,这种方法对于鱼眼镜头是不适用的,因为当$\theta$接近$\pi /2$时,透视模型会将点投影到无限远,无法通过传统的畸变模型消除这一奇点。因此,我们基于更通用的模型式(6)来进行校正。
我们将多项式投影模型式(6)和下面两个双参数模型进行了比较:
\[r= \frac{a}{b} \sin (b \theta) \tag{M1}\] \[r=\frac{a-\sqrt{a^2 - 4b\theta^2}}{2b\theta} \tag{M2}\]这两个模型出自论文“Two-View Geometry of Omnidirectional Cameras”。

我们在Fig2中列出了式(1)到式(5)的投影曲线(黑色实线),然后我们用P3、M1和M2去分别拟合这5条曲线,其中,P3是只考虑式(6)前两项的模型。我们设置$f=200$,对真实相机来说是一个合理的值。我们拟合的范围是0到$\theta_{\max}$之间,对式(1)到式(5),$\theta_{\max}$分别取$60^\circ,110^\circ,110^\circ,110^\circ,90^\circ$。区间$[0,\theta_{\max}]$被离散化,步长为$0.1^\circ$,使用Levenberg-Marquardt方法拟合M1和M2。从Fig2中可以看出,M1不适用于perspective projection(式(1))和stereographic projection(式(2)),M2不适用于orthogonal projection(式(5))。

在表1中,我们列出了最大近似误差。P9考虑了式(6)的前五项。从表1可以看出,P3的近似程度要好于双参数模型。如果要对5个投影模型都能很好的近似,则需要P9。这些结果表明,我们提出的模型是合理的。
4.CALIBRATING THE GENERIC MODEL
这部分主要是相机参数的计算过程。该校正方法基于一个已知位置的平面物体(个人注解:比如棋盘格校正板)。
4.A.Calibration Algorithm
校正过程一共分为4步。我们假定从$N$个view中检测到$M$个控制点(个人注解:比如$N$张校正板图像,共$M$个角点)。对于每个view,都有一个旋转矩阵$\mathbf{R}_j$和一个平移向量$\mathbf{t}_j$可用于描述相机相对于校正平面的位置:
\[\mathbf{X}_c = \mathbf{R}_j \mathbf{X} + \mathbf{t}_j, \quad j = 1,...,N \tag{17}\]个人注解:外参校正。
校正平面位于$XY$平面,其上的控制点$i$的坐标为$\mathbf{X}^i = (X^i,Y^i,0)^{\top}$,其对应的齐次坐标为$\mathbf{x}_p^i = (X^i,Y^i,1)^{\top}$(个人注解:参见张正友标定法)。第$j$个view中,控制点在图像上的坐标为$\mathbf{m}_j^i = (u_j^i, v_j^i)^{\top}$。校正过程的前三步只计算了6个相机内参,表示为$\mathbf{p}_6 \hat{=} (k_1,k_2,m_u,m_v,u_0,v_0)$。仅在最后一步插入其他的模型参数。
👉Step 1: Initialization of internal parameters
第一步:初始化内参。
首先对$k_1$和$k_2$的值进行初始化。初始化的方法如下,用$r=k_1 \theta + k_2 \theta^3$去拟合式(2)、式(3)、式(4)中的某一个(个人注解:从式(2)到式(4)中自行选择一个预期的模型),通过拟合便可得到$k_1$和$k_2$的初始值。在拟合时,式(2)到式(4)中的参数$f$和$\theta$分别使用镜头制造商提供的标准焦距$f$和最大视角$\theta_{\max}$。然后,我们便可计算图像坐标系下的最大半径为$r_{\max} = k_1 \theta_{\max}+k_2 \theta^3_{\max}$(个人注解:半径的单位是实际的物理距离,比如mm)。
鱼眼镜头的图像通常是一个椭圆形(个人注解:下式是椭圆的公式):
\[\left( \frac{u-u_0}{a} \right)^2 + \left( \frac{v-v_0}{b} \right)^2 = 1\]$a,b$(单位是像素)是椭圆的长轴和短轴,这两个值可以从图像上获得。$m_u$初始化为$m_u = a / r_{\max}$,$m_v$初始化为$m_v = b/r_{\max}$。将主点$(u_0,v_0)^{\top}$初始化为图像的中心。
👉Step 2: Back-projection and computation of homographies
第二步:单应性矩阵的计算。
相机坐标系中的点记为$\tilde{\mathbf{x}}_j^i$。单应性矩阵$\mathbf{H}_j$定义为$s \tilde{\mathbf{x}}_j^i = \mathbf{H}_j \mathbf{x}_p^i$。
个人注解:和该博文不同,此处的单应性矩阵只是一个外参矩阵。
对于每个view $j$,按照如下步骤计算$\mathbf{H}_j$:
-
将点从像素坐标系转换到图像坐标系:
\[\begin{pmatrix} x_j^i \\ y_j^i \end{pmatrix} = \begin{bmatrix} 1/m_u & 0 \\ 0 & 1/m_v \end{bmatrix} \begin{pmatrix} u_j^i - u_0 \\ v_j^i - v_0 \end{pmatrix}\]然后将图像坐标系下的点转换为极坐标形式$(r_j^i,\varphi_j^i) \hat{=}(x_j^i,y_j^i)$,然后通过解$k_2(\theta_j^i)^3+k_1\theta_j^i-r_j^i=0$得到$\theta_j^i$。
- 有了$\theta$和$\varphi$之后,我们就能计算该点在相机坐标系下的坐标为$\tilde{\mathbf{x}}_j^i=(\sin \varphi_j^i \sin \theta_j^i, \cos \varphi_j^i \sin \theta_j^i, \cos \theta_j^i)^{\top}$。
- 有了世界坐标系下的点$\mathbf{x}_p^i$和相机坐标系下的点$\tilde{\mathbf{x}}_j^i$,我们可以通过数据归一化的线性算法初步计算得到一个$\mathbf{H}_j$(个人注解:这里是考虑view $j$上的所有点去拟合出来一个转换矩阵$\mathbf{H}_j$,矩阵计算的方法这里不再详述,作者引用了文献“Hartley, R. and Zisserman, A.: Multiple View Geometry, 2nd ed., Cambridge, 2003.”,或者参考该博文)。然后计算在view $j$中,世界坐标系下每个点经过矩阵转换后在相机坐标系下的点$\hat{\mathbf{x}}_j^i = \mathbf{H}_j \mathbf{x}_p^i / | \mathbf{H}_j\mathbf{x}_p^i |$。
- 通过最小化$\sum_i \sin ^2 \alpha_j^i$来refine单应性矩阵$\mathbf{H}_j$,其中$\alpha_j^i$是两个单位向量$\tilde{\mathbf{x}}_j^i$和$\hat{\mathbf{x}}_j^i$之间的夹角。
个人注解:解释下第2步,在球坐标系中:
将球坐标变换为直角坐标:
$x = r \sin \theta \cos \varphi$
$y = r \sin \theta \sin \varphi$
$z = r \cos \theta$
第2步的公式中省略了半径$r$,且第2步的坐标是按$\{y,x,z \}$排列的,但是这些都不重要,后面只是用到两个单位向量的夹角。
👉Step 3: Initialization of external parameters
第三步:初始化外参。
我们可以从单应性矩阵$\mathbf{H}_j$中提取出相机外参的初始值。
\[s \tilde{\mathbf{x}}_j^i = \begin{bmatrix} \mathbf{R}_j & \mathbf{t}_j \end{bmatrix} \begin{pmatrix} X^i \\ Y^i \\ 0 \\ 1 \end{pmatrix} = \begin{bmatrix} \mathbf{r}_j^1 & \mathbf{r}_j^2 & \mathbf{t}_j \end{bmatrix} \begin{pmatrix} X^i \\ Y^i \\ 1 \end{pmatrix}\]其中,
\[\mathbf{H}_j = \begin{bmatrix} \mathbf{h}_j^1 & \mathbf{h}_j^2 & \mathbf{h}_j^3 \end{bmatrix} = \begin{bmatrix} \mathbf{r}_j^1 & \mathbf{r}_j^2 & \mathbf{t}_j \end{bmatrix}\]旋转矩阵定义为:
\[\mathbf{R}_j = \begin{bmatrix} \mathbf{r}_j^1 & \mathbf{r}_j^2 & \mathbf{r}_j^3 \end{bmatrix}\]其每一列的计算公式为:
\[\mathbf{r}_j^1 = \lambda_j \mathbf{h}_j^1\] \[\mathbf{r}_j^2 = \lambda_j \mathbf{h}_j^2\] \[\mathbf{r}_j^3 = \mathbf{r}_j^1 \times \mathbf{r}_j^2\]平移向量的公式为:
\[\mathbf{t}_j = \lambda_j \mathbf{h}_j^3\]其中比例因子$\lambda_j$的计算为:
\[\lambda_j = \text{sign}(H_j^{3,3}) / \| \mathbf{h}_j^1 \|\]sign函数会判断矩阵$\mathbf{H}_j$第3行第3列数值的符号。由于估计误差,得到的旋转矩阵可能不是正交的。因此,我们使用SVD对旋转矩阵进行正交化处理,并将其作为$\mathbf{R}_j$的初始值。
👉Step 4: Minimization of projection error
第四步:最小化投影误差。
如果使用参数更多的$\mathbf{p}_{23}$或$\mathbf{p}_9$模型,则把剩余的参数都初始化为0。至此,我们已经初始化了所有的相机内参和外参,接下来我们便可以利用式(17)、式(7)或式(10)、式(11)来计算世界坐标系到像素坐标系的转换$\hat{\mathbf{m}}_j^i = \mathcal{P}_j(\mathbf{X}^i)$。我们通过最小化测量点和建模点之间的平方距离来refine相机参数:
\[\sum_{j=1}^N \sum_{i=1}^M d (\mathbf{m}_j^i, \hat{\mathbf{m}}_j^i)^2 \tag{18}\]求解使用Levenberg-Marquardt算法。
4.B.Modification for Circular Control Points
为了实现精确的校正,作者使用的校正板背景是黑色的,上面有白色的圆(见Fig4),因为这样投影圆圈的质心可以以亚像素级别的精度被检测到。但是存在一个问题,投影圆圈的质心并不是原始圆圈的质心。因此在式(18)中,$\mathbf{m}_j^i$为原始圆圈的质心,我们需要对式(18)中投影圆圈的质心$\hat{\mathbf{m}}_j^i$进行进一步的调整。
个人注解:在棋盘格校正板中,控制点就是角点。而作者这里用的校正板,控制点是白色圆圈的质心。
首先,我们用下式表示一个圆心为$(X_0,Y_0)$,半径为$R$的圆内的所有点(即对圆进行参数化表示):
\[\mathbf{X}(\varrho,\alpha) = (X_0 + \varrho \sin \alpha, Y_0 + \varrho \cos \alpha, 0)^{\top}, \ \varrho \in [0,R], \ \alpha \in [0, 2\pi]\]调整后的投影质心$\hat{\mathbf{m}}$可通过下式计算:
\[\hat{\mathbf{m}} = \frac{\int_0^R \int_0^{2\pi} \hat{\mathbf{m}}(\varrho, \alpha) |\det \mathbf{J}(\varrho, \alpha)| \, d\alpha \, d\varrho}{\int_0^R \int_0^{2\pi} |\det \mathbf{J}(\varrho, \alpha)| \, d\alpha \, d\varrho} \tag{19}\]其中,$\hat{\mathbf{m}}(\varrho,\alpha) = \mathcal{P}(\mathbf{X}(\varrho,\alpha))$,$\mathbf{J}(\varrho,\alpha)$是$\mathcal{P} \circ \mathbf{X}$的雅可比矩阵。
5.CALIBRATION EXPERIMENTS
5.A.Conventional and Wide-Angle Lens Camera
将我们提出的相机模型和论文“Geometric camera calibration using circular control points”提出的相机模型进行了比较。该论文提出的相机模型是一个skew-zero的针孔模型,带有4个畸变参数,我们用$\boldsymbol{\delta}_8$表示这个模型。
第一个实验使用论文“Geometric camera calibration using circular control points”提供的数据。它是一个单张图像,图像中的校正目标是两个正交的平面,每个平面都有256个圆形控制点。所用相机为单色CCD相机,配备8.5毫米的Cosmicar镜头。第二个实验使用的是Sony DFW-VL500相机和广角转换镜头,总焦距为3.8毫米。在这个实验中,我们使用了6张包含校正目标的图像。总共有1328个控制点,可以通过计算它们的灰度质心来定位它们。
RMS残差(即测量点和建模点距离的均方根)的统计结果见表2。其中,$\boldsymbol{\delta}_8$和$\mathbf{p}_9$的自由度都是8。尽管$\mathbf{p}_9$没有考虑畸变,但其效果仍略优于$\boldsymbol{\delta}_8$。

然而,在第一个实验中,整个模型可能部分地适应了校正数据的系统误差。这是由于只有一张图像的测量结果,其中照明不均匀,所有角落都没有被控制点覆盖。Fig3是$\mathbf{p}_{23}$的校正结果,可以看到,由于不均匀的照明,右下角的点不够准确(Fig3(b))。

在第二个实验中,校正数据质量更高,因此,完整的模型可能更有用。$\mathbf{p}_{23}$的RMS投影误差为0.049个像素,$\mathbf{p}_9$的RMS投影误差为0.071个像素。
最后,我们也评估了$\mathbf{p}_{23}$的反向模型误差(即由一阶近似导致的误差,见第2.C部分)。评估方式为先反向投影每个像素,然后再重新做正向投影。第一个相机的最大误差为$2.1 \cdot 10^{-5}$个像素,第二个相机的最大误差为$4.6 \cdot 10^{-4}$个像素。两个误差值都很小,说明在实践中,我们可以忽视反向模型的误差。
5.B.Fish-Eye Lens Cameras
第一个实验的鱼眼镜头是等距镜头(equidistance lens),标准焦距为1.178毫米,安装在Watec 221S CCD彩色相机上。校正板大小为$2 \times 3m^2$,背景是黑色,上面有白色的圆圈,圆圈半径为60毫米。校正图像为8-bit的灰度图像,大小为$640\times 480$个像素。

如Fig4所示,只使用一张校正板图像,也可实现对鱼眼镜头的校正。在这个例子中,我们使用了$\mathbf{p}_6$模型和60个控制点。为了得到更准确的校正结果,我们还测试使用了12张校正板图像,共680个点,结果见表3。且由于测量数量众多,所以不存在过拟合的风险。

畸变的评估见Fig5:
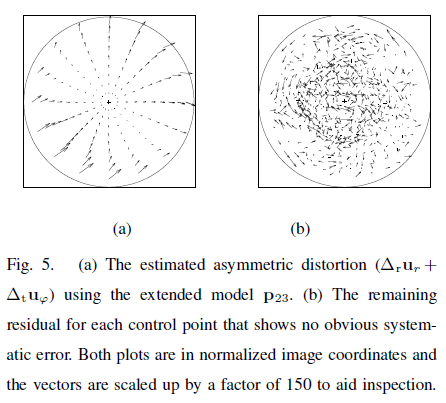
第二个实验的鱼眼镜头是Omnitech Robotics生产的ORIFL190-3镜头。该镜头的FOV为190度,并且其明显和equidistance projection模型有差异。镜头安装在Point Grey Dragonfly digital彩色相机上,分辨率为$1024 \times 768$个像素,校正目标和第5.A部分一样。结果见表3的第二行,使用了12张校正板图像和1780个控制点。
同样也评估了$\mathbf{p}_{23}$的反向模型误差,第一个相机的最大误差为$9.7 \cdot 10^{-6}$个像素,第二个相机的最大误差为$3.4 \cdot 10^{-3}$。
5.C.Synthetic Data
为了评估我们所提出的校正方法的鲁棒性,我们在合成数据(synthetic data)上也进行了实验。我们从真实的鱼眼镜头中获取相机参数的真实值(来自Fig5中的设置)。我们使用完整的相机模型,使用12张合成的校正图像,共680个圆形控制点,其中,校正板背景的灰度值设为5,圆形区域的灰度值设为180。为了使合成图像更贴近真实图像,我们进行了高斯模糊($\sigma=1$),并归一化到0-255的灰度值。
首先,我们评估了第4.B部分提到的质心调整的有效性。实验发现,调整前后的质心在RMS距离上差了0.45个像素,明显高于表3中的误差。这表明,如果没有质心调整,估计的相机参数将有偏差。
其次,我们通过向合成图像中添加高斯噪声来评估噪声对校正的影响,在每个噪声级别,执行10次校正实验。噪声的标准差在0到15个像素之间。首先通过使用固定阈值对噪声图像进行阈值处理,然后再从噪声图像中定位控制点。然后通过计算灰度加权质心来测量每个控制点的质心。结果见Fig6。

6.CONCLUSION
不再赘述。
7.原文链接
👽A Generic Camera Model and Calibration Method for Conventional, Wide-Angle, and Fish-Eye Lenses
