本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.INTRODUCTION
通过研究通道间的关系,提出了新的框架单元,称为SE block(Squeeze-and-Excitation),其结构见下:
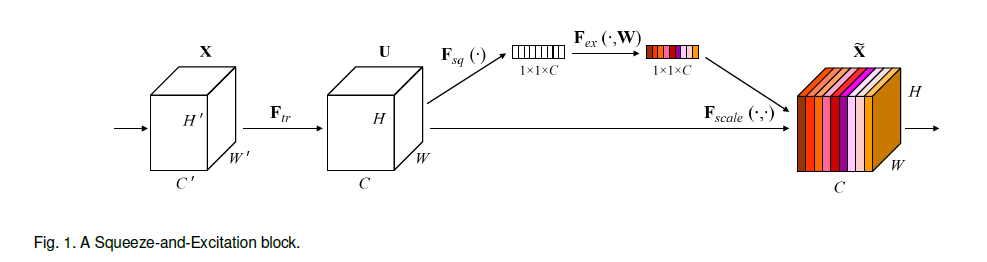
$\mathbf{F}_{tr}$表示从feature map $\mathbf{X}$到feature map $\mathbf{U}$的转换,比如$\mathbf{F}_{tr}$可以是卷积操作。$\mathbf{F}_{sq}$表示squeeze操作,即SENet中S的含义,其将$\mathbf{U}$压缩为$1\times 1 \times C$,比如$\mathbf{F}_{sq}$可以是global average pooling操作。$\mathbf{F}_{ex}$表示excitation操作,即SENet中E的含义,其通过转换得到每个通道的权重,比如$\mathbf{F}_{ex}$可以是多个全连接层。最后,通过$\mathbf{F}_{scale}$将权重应用于$\mathbf{U}$的每个通道,得到SE block的输出$\tilde{\mathbf{X}}$。
2.RELATED WORK
不再详述。
3.SQUEEZE-AND-EXCITATION BLOCKS
$\mathbf{F}_{tr}$表示从$\mathbf{X}\in \mathbb{R}^{H’\times W’\times C’}$到$\mathbf{U}\in \mathbb{R}^{H\times W \times C}$的转换。我们将$\mathbf{F}_{tr}$设置为卷积操作。假设$\mathbf{V}=[\mathbf{v}_1,\mathbf{v}_2,…,\mathbf{v}_C]$表示一组卷积核,其中,$\mathbf{v}_c$表示第$c$个卷积核。输出$\mathbf{U}=[\mathbf{u}_1,\mathbf{u}_2,…,\mathbf{u}_C]$的计算如下:
\[\mathbf{u}_c=\mathbf{v}_c * \mathbf{X}=\sum_{s=1}^{C'}\mathbf{v}_c^s * \mathbf{x}^s \tag{1}\]其中,$*$表示卷积,$\mathbf{v}_c = [\mathbf{v}_c^1,\mathbf{v}_c^2,…,\mathbf{v}_c^{C’}]$,$\mathbf{X} = [\mathbf{x}^1,\mathbf{x}^2,…,\mathbf{x}^{C’}]$,$\mathbf{u}_c \in \mathbb{R}^{H \times W}$。式(1)中偏置项被省略。
3.1.Squeeze: Global Information Embedding
因为卷积利用到的信息是局部的,所以在squeeze阶段,我们考虑使用全局信息,因此我们使用了global average pooling,用公式表示为:
\[z_c = \mathbf{F}_{sq}(\mathbf{u}_c)=\frac{1}{H \times W}\sum_{i=1}^H \sum_{j=1}^W u_c (i,j) \tag{2}\]其中,$\mathbf{z} \in \mathbb{R}^C$,$z_c$是$\mathbf{z}$中的第$c$个元素。
3.2.Excitation: Adaptive Recalibration
excitation阶段为两个全连接层,第一个全连接层将神经元数量从$C$降低为$\frac{C}{r}$个,激活函数为ReLU,第二个全连接层将神经元数量从$\frac{C}{r}$恢复为$C$个,然后通过一个sigmoid激活函数(以保证通道权重在[0,1]之间)。用公式可表示为:
\[\mathbf{s} = \mathbf{F}_{ex}(\mathbf{z,W}) = \sigma(g(\mathbf{z,W})) = \sigma(\mathbf{W}_2 \delta (\mathbf{W}_1\mathbf{z})) \tag{3}\]其中,$\delta$表示ReLU函数,$\mathbf{W}_1 \in \mathbb{R}^{\frac{C}{r}\times C}, \mathbf{W}_2 \in \mathbb{R}^{C \times \frac{C}{r}}$。SE block的最终输出为:
\[\tilde{\mathbf{x}}_c=\mathbf{F}_{scale}(\mathbf{u}_c,\mathbf{s}_c) = \mathbf{s}_c \mathbf{u}_c \tag{4}\]其中,$\tilde{\mathbf{X}}=[\tilde{\mathbf{x}}_1,\tilde{\mathbf{x}}_2,…,\tilde{\mathbf{x}}_C]$,$\mathbf{F}_{scale}(\mathbf{u}_c,\mathbf{s}_c)$表示$\mathbf{s}_c$和feature map $\mathbf{u}_c \in \mathbb{R}^{H \times W}$之间进行的channel-wise的乘法。
3.3.Instantiations
本部分介绍了几个将SE block和其他网络模块相结合的例子。
Fig2是将SE block和Inception模块相结合,得到SE-Inception模块:
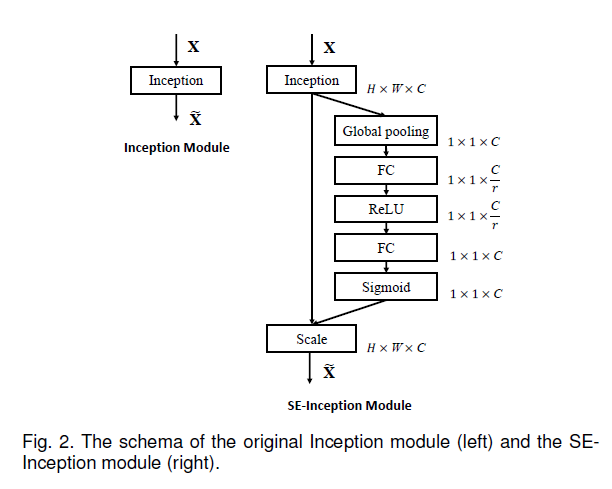
Fig3是将SE block和残差模块相结合,得到SE-ResNet模块:

表1列出了SE-ResNet-50和SE-ResNeXt-50的网络结构:

4.MODEL AND COMPUTATIONAL COMPLEXITY
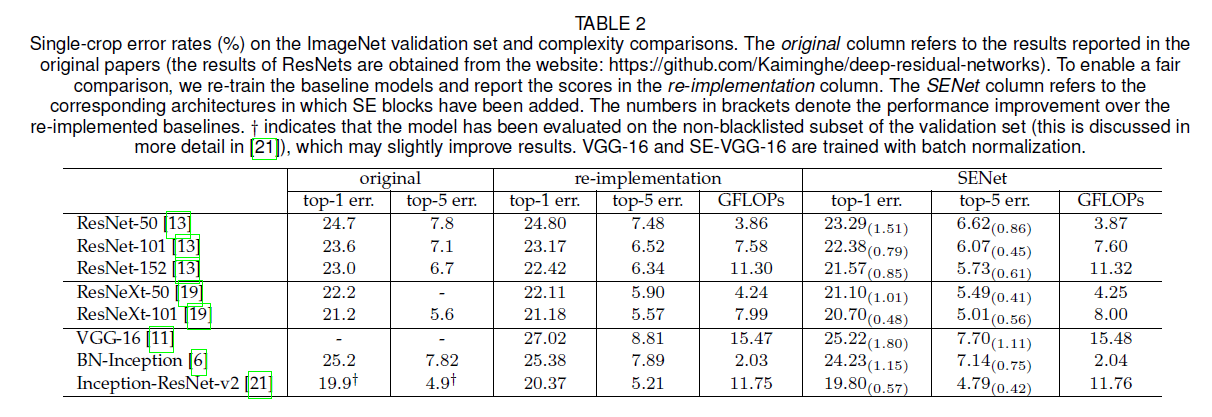
如表2所示,添加SE block只是轻微的增加了计算复杂度,同时模型性能有较显著的提升。
5.EXPERIMENTS
5.1.Image Classification
我们先在ImageNet 2012数据集上进行了实验,该数据集包含1.28M的训练图像和50K的验证图像,共计1000个类别。我们在训练集上进行了训练,并在验证集上汇报了top-1和top-5错误率。
每个baseline网络和其对应的SE变体在训练时都使用一样的优化策略。对于数据扩展,我们使用了随机裁剪和随机水平翻转。对于Inception-ResNet-v2和SE-Inception-ResNet-v2,随机裁剪到$299 \times 299$,对于其他网络,随机裁剪到$224 \times 224$。每张输入图像都通过减去RGB通道均值来进行归一化。momentum=0.9,minibatch size=1024。初始学习率设置为0.6,之后每30个epoch缩小10倍。模型从头开始训练了100个epoch。参数$r$默认设置为16。
在评估模型时,对于Inception-ResNet-v2和SE-Inception-ResNet-v2,先将图像的短边resize到352,然后中心裁剪$299 \times 299$大小;对于其他网络,先将图像短边resize到256,然后中心裁剪$224 \times 224$大小。
👉Network depth.
结果见表2。
👉Integration with modern architectures.
结果见表2。
👉Mobile setting.
我们还比较了两个典型的专为移动端设计的网络:MobileNet和ShuffleNet。对于这些实验,minibatch size=256,不使用过于激进的数据扩展和正则化。momentum=0.9,初始学习率为0.1,之后每当验证损失不再下降时,学习率减小10倍。一共训练了约400个epoch。结果见表3。

👉Additional datasets.
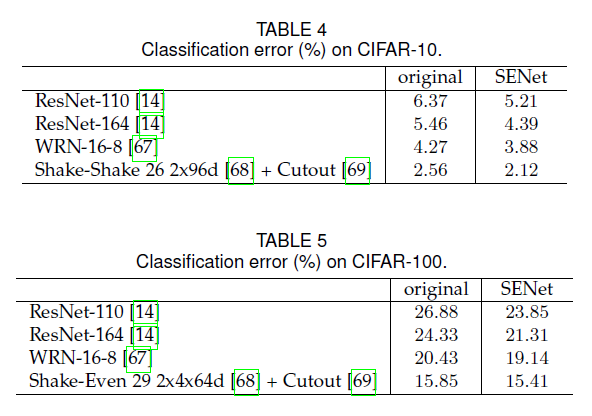
5.2.Scene Classification
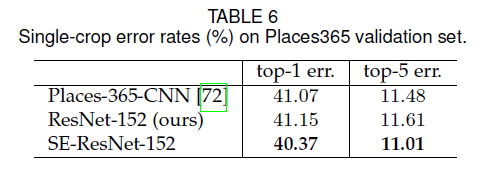
5.3.Object Detection on COCO
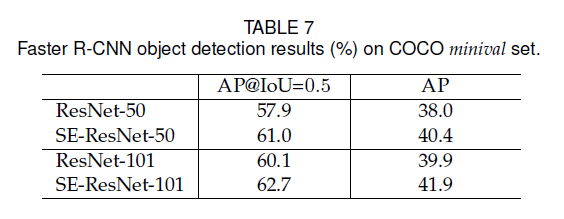
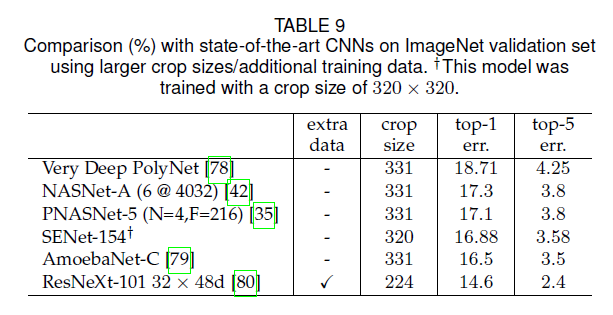
5.4.ILSVRC 2017 Classification Competition
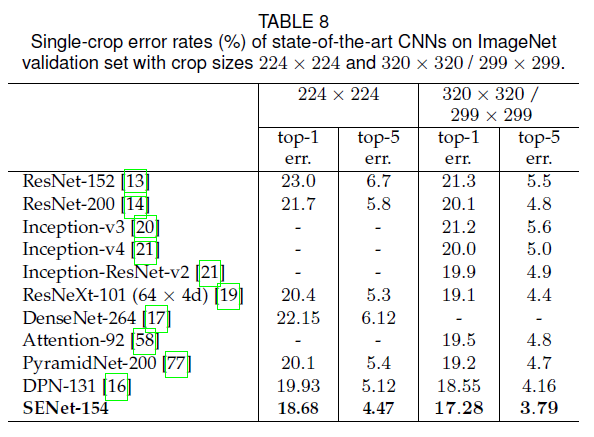
在ResNet-152的基础上得到64x4d ResNeXt-152,再在64x4d ResNeXt-152基础上添加SE block得到SENet-152。在SENet-152的基础上又做了如下修改,得到表8中的SENet-154:
- 将每个bottleneck building block中第一个$1\times 1$卷积的通道数减半,在最小化对性能影响的前提下,降低模型的计算成本。
- 将第一个$7 \times 7$卷积替换为3个连续的$3 \times 3$卷积。
- 将$1\times 1$、步长为2的下采样替换为$3\times 3$、步长为2的下采样。
- 在分类层之前添加一个dropout层以降低过拟合,dropout ratio为0.2。
- 在训练阶段使用了LSR。
- 在训练的最后几个epoch,所有BN层的参数都被冻结,以此确保训练和测试的一致性。
- 为了使用更大的batch size(2048),训练在8个服务器(64块GPU)上并行运行,初始学习率设置为1.0。
6.ABLATION STUDY
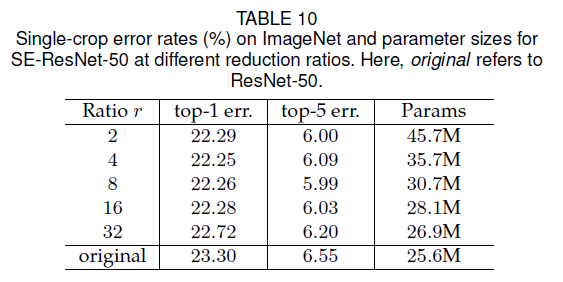
6.1.Reduction ratio
reduction ratio $r$见第3.2部分。
6.2.Squeeze Operator
我们比较了global average pooling和global max pooling,结果见表11:

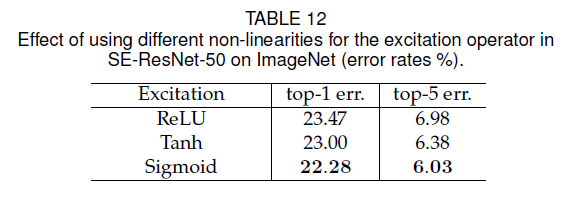
6.3.Excitation Operator
比较了Sigmoid、ReLU和Tanh,结果见表12:
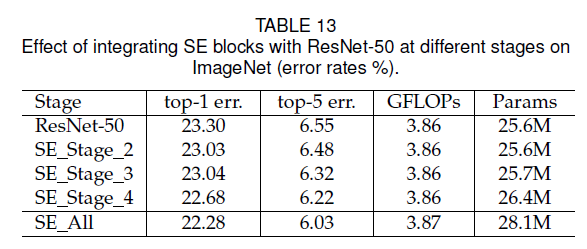
6.4.Different stages
我们分别在ResNet-50的不同阶段插入SE block,结果见表13:
6.5.Integration strategy
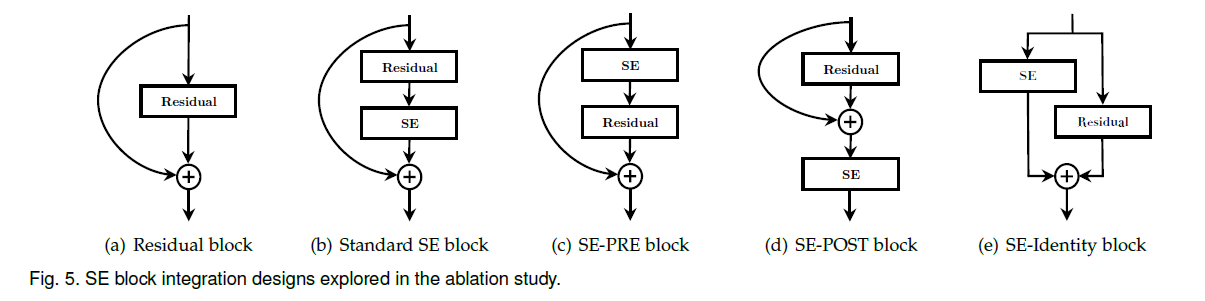
Fig5(a)是残差块的结构,Fig5(b)是SE block嵌入残差块的标准形式,Fig5(c)-(e)是3种变体。
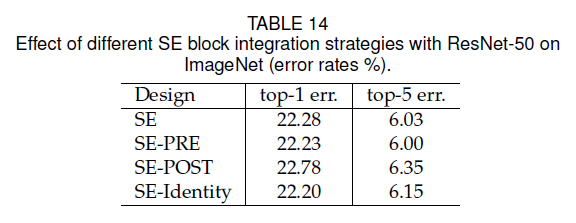
Fig5中列出的几种SE block都是在residual unit的外面,我们还测试了将SE block放在residual unit里面,放在$3\times 3$卷积之后,结果见表15:
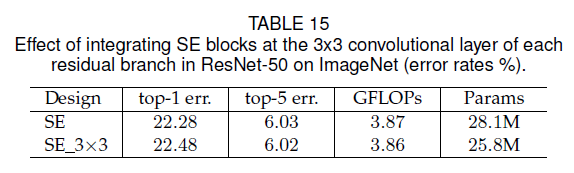
7.ROLE OF SE BLOCKS
7.1.Effect of Squeeze
实验了去掉Squeeze的情况,结果见表16:
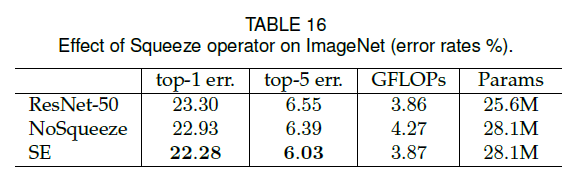
7.2.Role of Excitation
为了研究SE block中Excitation的作用,我们研究了SE-ResNet-50的激活值,我们想了解其在不同类别的图像之间以及同一类别内不同图像之间的变化。
我们首先考虑不同类别之间的变化,选择了4个类别,分别是goldfish、pug、plane和cliff:

我们在验证集中为每个类别各抽取50个样本,然后从每个stage最后一个SE block(下采样之前)中均匀采样50个通道并计算其平均激活值,其结果绘制在Fig6中。作为参考,我们还绘制了所有1000个类别的平均激活值。
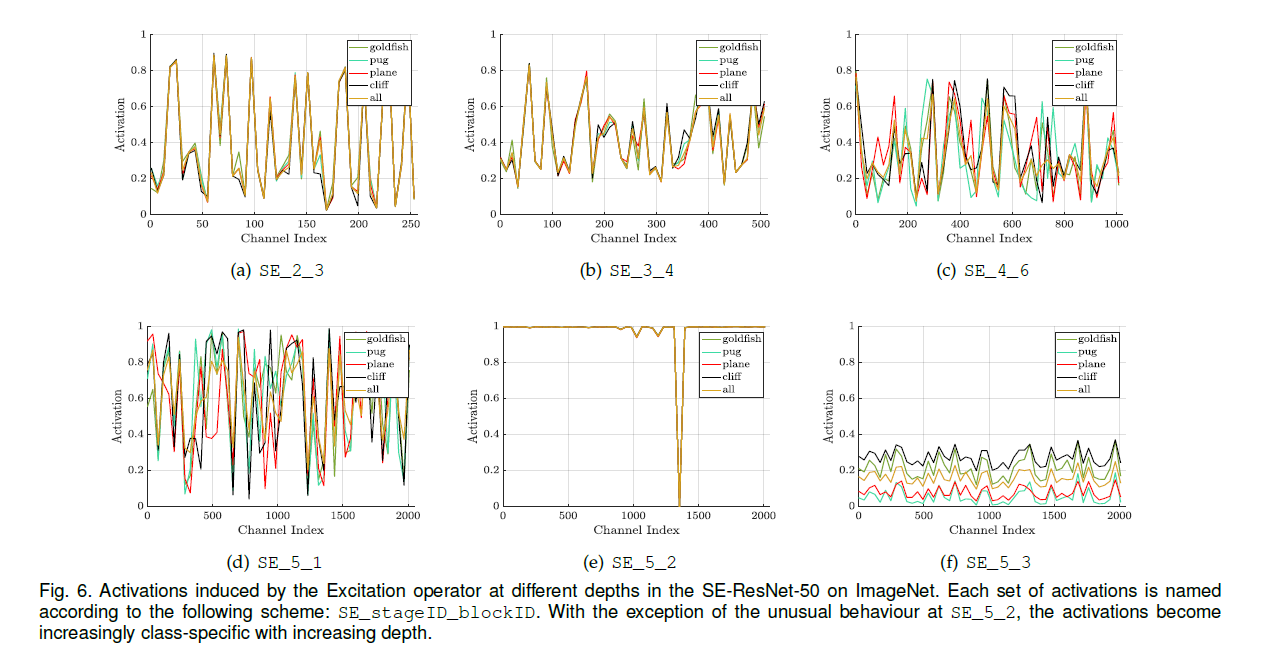
可以看到,随着网络深度的加深,每个通道的数值变得更加特定于类别。
相同的分析在同一类别内的不同图像之间也进行了,激活值的均值和标准差分布见Fig7:
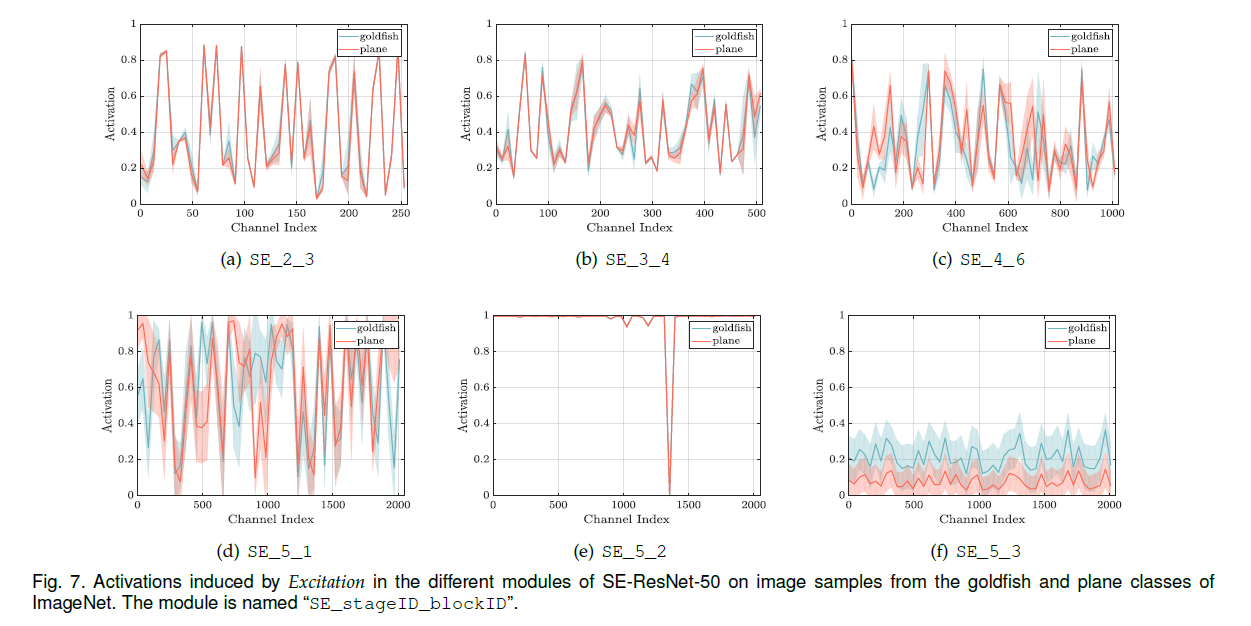
这些分析结果表明SE block的动态行为不仅在不同类别之间有所不同,在同一类别的实例之间也存在差异。
8.CONCLUSION
不再赘述。