本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
评估CNN模型的两个重要指标:精度和计算复杂度。衡量计算复杂度最常用的是FLOPs。但FLOPs并不完全等同于推理速度,相同的FLOPs可能会有不同的推理速度,如Fig1(c)(d)所示。因此,使用FLOPs作为计算复杂度的唯一指标可能会导致次优设计。
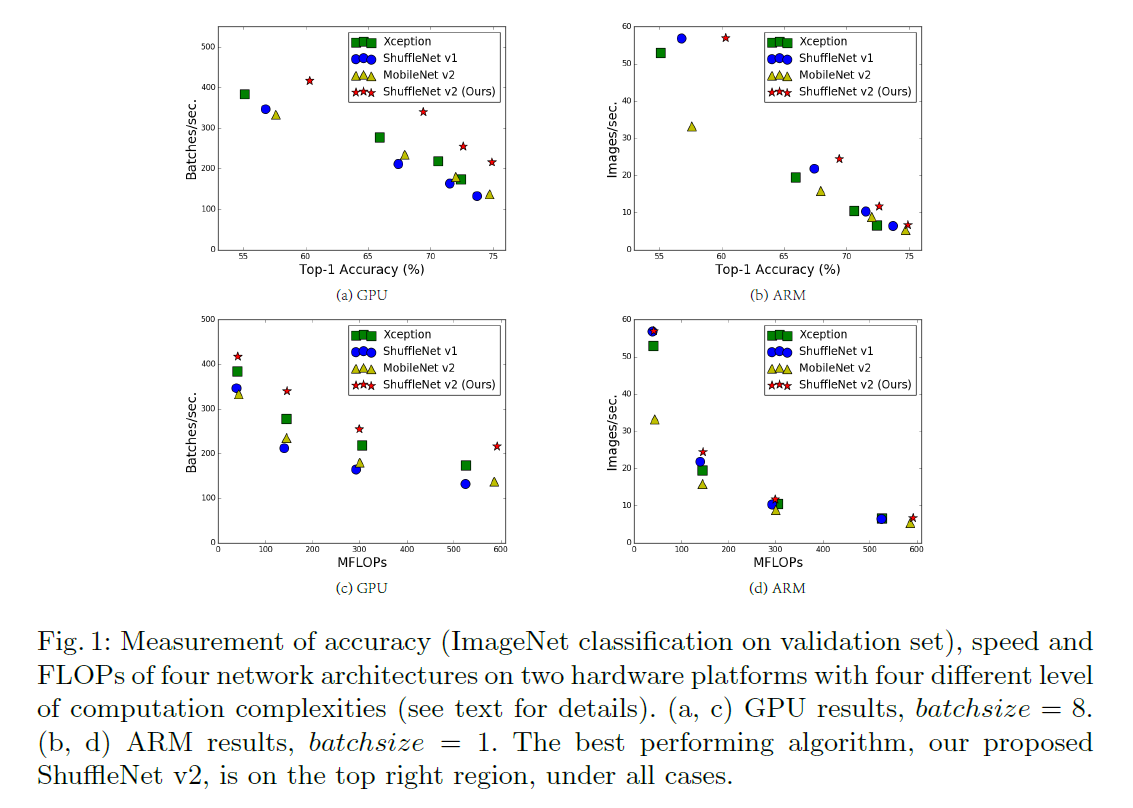
FLOPs和推理速度不能完全等同可归于两个重要原因:
- 一些对推理速度有重要影响的因素未被FLOPs考虑在内。这些影响推理速度的重要因素有MAC、并行程度等。
- 由于平台的差异,相同的FLOPs可能会有不同的运行时间。
基于此,要想设计一个高效的网络架构,我们提出了两点原则:1)使用更加直接的指标,比如推理速度,而不是FLOPs;2)这些指标应该在目标平台上被评估。
2.Practical Guidelines for Efficient Network Design
配置信息:
- GPU:单个NVIDIA GeForce GTX 1080Ti,CUDNN 7.0。
- ARM:Qualcomm Snapdragon 810,评估时使用单线程。
- 开启全优化选项(比如tensor fusion)。
- 输入图像大小为$224 \times 224$。
- 每个网络的权重都是随机初始化的。
- 运行时间取100次的平均值。
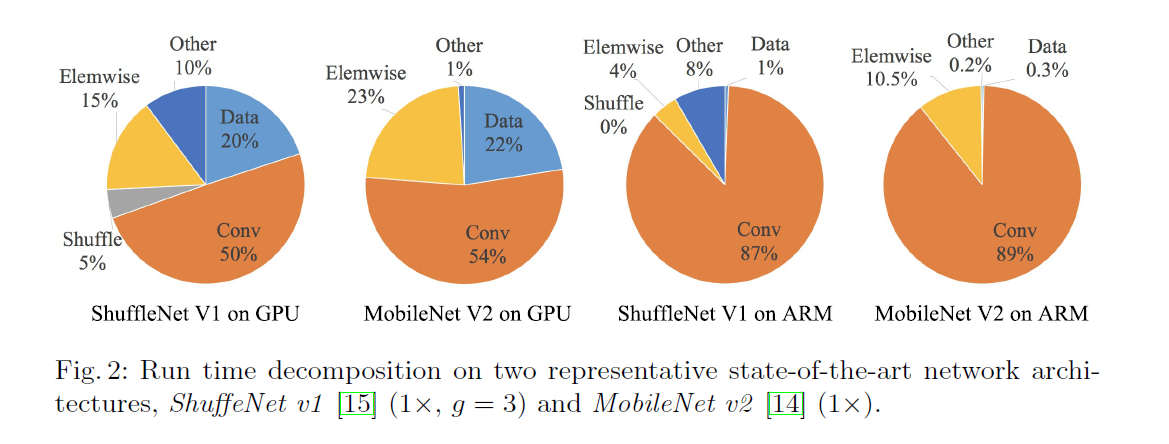
从Fig2我们注意到,FLOPs只衡量了卷积部分,虽然卷积部分确实耗时最多,但是其他操作比如data I/O,data shuffle和element-wise操作(比如AddTensor,ReLU等)也消耗了很多时间。因此,FLOPs并不能用于准确的评估实际的运行时间。
我们分析出几个高效网络架构设计的实用准则:
👉准则一:相等的通道宽度可以最小化MAC。
现代网络通常使用深度分离卷积,其中pointwise卷积(即$1\times 1$卷积)占据了主要的计算复杂度。$1 \times 1$卷积的形状由两个参数决定:输入通道数$c_1$和输出通道数$c_2$。假设feature map的大小为$h \times w$,则$1\times 1$卷积的FLOPs为$B=hwc_1c_2$。
为了简化起见,假设计算设备的缓存足够大,可以存储整个feature map和参数。那么,MAC,也就是内存访问操作的次数,为$MAC=hw(c_1+c_2)+c_1c_2$。其中,第一项对应输入/输出feature map的内存访问,第二项对应卷积核权重的内存访问。
\[MAC \geqslant 2 \sqrt{hwB} + \frac{B}{hw} \tag{1}\]因此,在给定FLOPs时,MAC存在下界。当输入通道数和输出通道数相等时,MAC可以达到这个下界。
这个结论是理论上的。在实践中,很多设备的缓存并不足够大。因此,现代计算库通常采用复杂的blocking策略来充分利用缓存机制。所以,实际的MAC可能会偏离理论值。为了验证上述结论,进行了如下实验:构建一个基准网络,由10个基本模块重复堆叠而成。每个模块包含两个卷积层:第一个卷积层有$c_1$个输入通道和$c_2$个输出通道,第二个卷积层则相反(即输入通道数为$c_2$,输出通道数为$c_1$)。
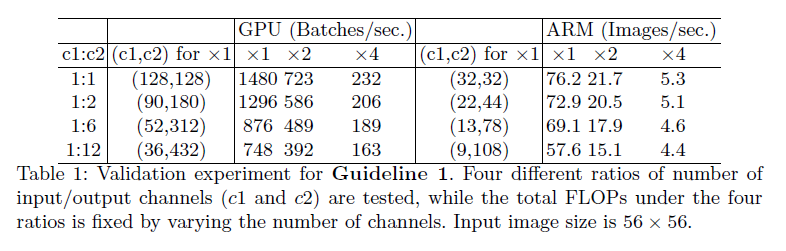
表1在固定总FLOPs的情况下,列出了不同$c_1:c_2$比例时的运行速度。结果表明,当$c_1:c_2$趋近于$1\times 1$时,MAC更小,网络的推理速度更快。
分组卷积是现代网络架构的核心。它通过将密集卷积(所有通道间相连)改为稀疏卷积(仅组内的通道间相连)来降低计算复杂度(即FLOPs)。一方面,在固定FLOPs的情况下,这允许使用更多通道,从而提升网络性能,提高精度。但另一方面,通道数的增加也会导致更大的MAC。
$1\times 1$分组卷积的MAC与FLOPs之间的关系为:
\[\begin{align*} MAC &= hw(c_1+c_2)+\frac{c_1c_2}{g} \\&= hwc_1 + \frac{Bg}{c_1} + \frac{B}{hw} \end{align*} \tag{2}\]其中,$g$是组数,且$B=hwc_1c_2/g$表示FLOPs。很容易看出,在输入形状$c_1 \times h \times w$和计算成本$B$固定的情况下,随着$g$的增加,MAC也随之增加。
为了研究实际影响,我们搭建了一个基准网络,由10个pointwise分组卷积层堆叠而成。
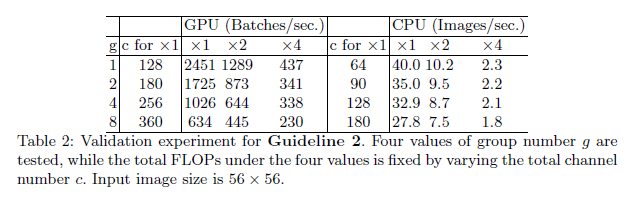
在表2中,通过调整通道数量来保证总的FLOPs基本不变。从表2可以看出,分组数量越多,推理速度反而越慢。
👉准则三:网络碎片化会降低并行度。
在一些网络架构中,比如GoogLeNet系列,每个网络模块通常采用“多路径”结构。在这种结构下,使用了大量的小算子(这里称为“碎片化算子”),而不是少量的大算子。尽管这种碎片化结构已被证明对提升精度有益,但它会降低效率,因为它不利于像GPU这样具有强大并行计算能力的设备。此外,它还会引入额外的开销,比如kernel启动和同步操作。
GoogLeNet系列博客:
为了量化网络碎片化对效率的影响,我们评估了一系列具有不同碎片化程度的网络模块,见Appendix Fig1:
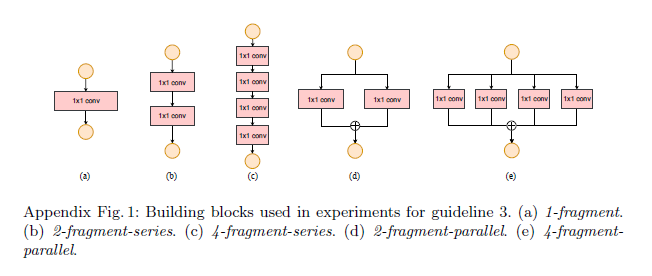
每个模块重复堆叠10次,结果见表3:
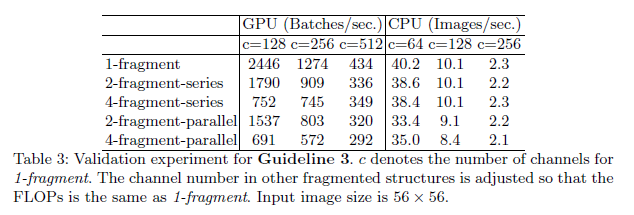
👉准则四:element-wise操作不可忽略。
如Fig2所示,在轻量级模型中,element-wise操作占据了相当多的运行时间,尤其是在GPU上。这些操作包括ReLU、AddTensor、AddBias等。它们的FLOPs很小,但对应的MAC却很高。特别的,我们还将深度分离卷积视为element-wise操作,因为它同样具有较高的MAC/FLOPs比值。
为了验证这一点,我们在ResNet中的bottleneck unit(即$1\times 1$卷积$\to 3 \times 3$卷积$\to 1\times 1$卷积,并带有ReLU和shortcut connection)上进行了实验。尝试分别移除ReLU和shortcut,结果见表4:
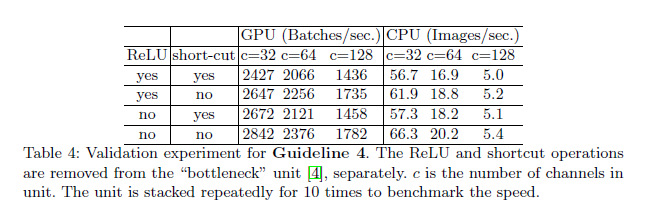
👉结论和讨论。
因此,我们得出结论,一个高效的网络架构应该满足以下几点:
- 相等的通道宽度。
- 注意分组卷积的代价。
- 减少网络碎片化。
- 减少element-wise操作。
这些特性依赖于平台,超出了FLOPs的范畴。因此,在实际网络设计中应当被考虑进去。近期的轻量化CNN架构大多只考虑了FLOPs这一指标,而忽略了上面提到的特性。
3.ShuffleNet V2: an Efficient Architecture
👉Review of ShuffleNet v1
ShuffleNet v1请见:【论文阅读】ShuffleNet:An Extremely Efficient Convolutional Neural Network for Mobile Devices,其模块结构见Fig3(a)和Fig3(b)。
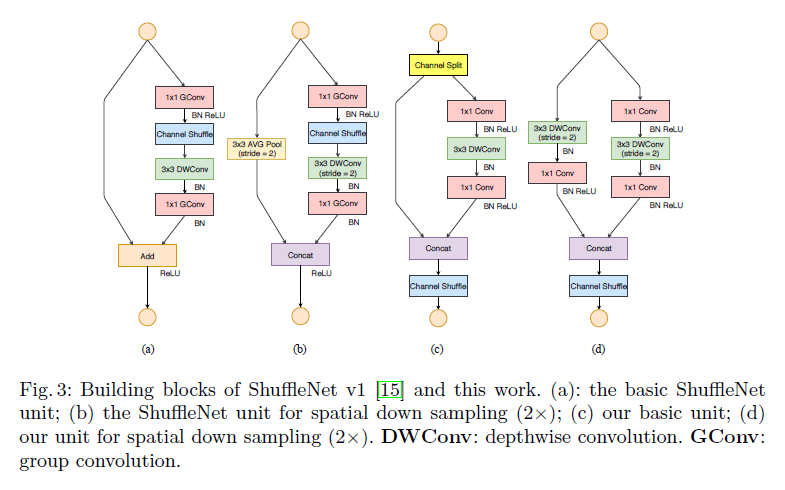
正如我们在第2部分所讨论的,pointwise分组卷积和bottleneck结构会增加MAC(见准则一和准则二)。这个代价是不能忽略的,尤其是对轻量化模型。同时,使用过多的分组也违背了准则三。shortcut中的element-wise加操作违背了准则四。
👉Channel Split and ShuffleNet V2
为了解决上述问题,我们引入了channel split,如Fig3(c)所示。在每个unit的开始,输入通道数为$c$,其会被一分为二,两个分支的通道数分别为$c-c’$和$c’$。为了遵循准则三,其中一个分支没有任何操作,另一个分支只包含3个卷积,且输入和输出通道数相等,这也符合准则一。两个$1\times 1$卷积不再是分组卷积,这也遵守了准则二。
两个分支最后被concat在一起。接着是channel shuffle。再然后就是下一个unit的开始。
对于空间下采样,unit改为如Fig3(d)所示的形式,移除了channel split,因此输出通道数会翻倍。
我们将使用Fig3(c)和Fig3(d)的网络称为ShuffleNet V2。
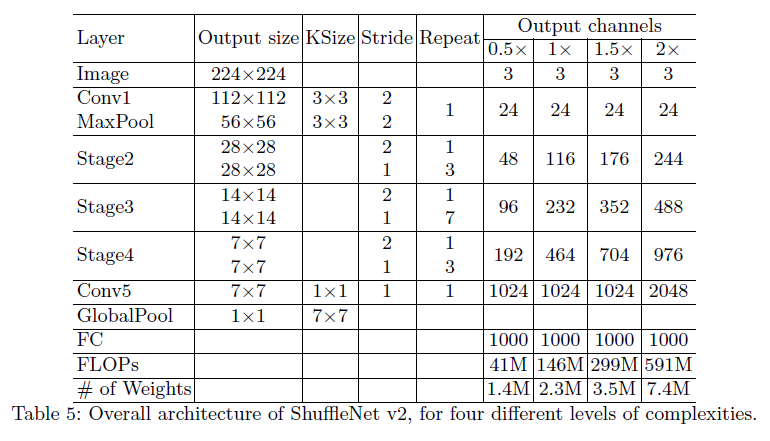
在表5中,通过控制通道的数量来产生不同计算复杂度的网络。
👉Analysis of Network Accuracy
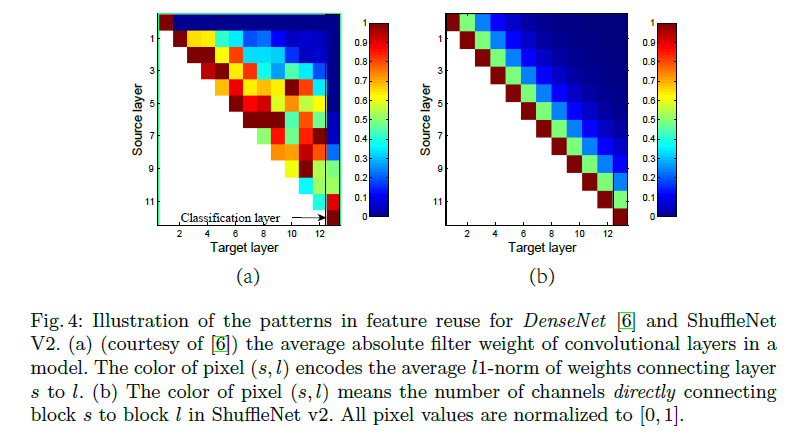
Fig4(a)是DenseNet,Fig4(b)是ShuffleNet V2。Fig4怎么看可以参照:Discussion。Fig4主要是想说明,DenseNet采用密集连接实现特征的强复用,但也会带来冗余和开销,而ShuffleNet V2采用“近强远弱”的特征复用模式,既保留了高精度所需的复用优势,又更加的高效。
4.Experiment
我们在ImageNet 2012分类数据集上进行了消融实验。所有网络都设置为4种计算复杂度:40MFLOPs、140MFLOPs、300MFLOPs、500MFLOPs。
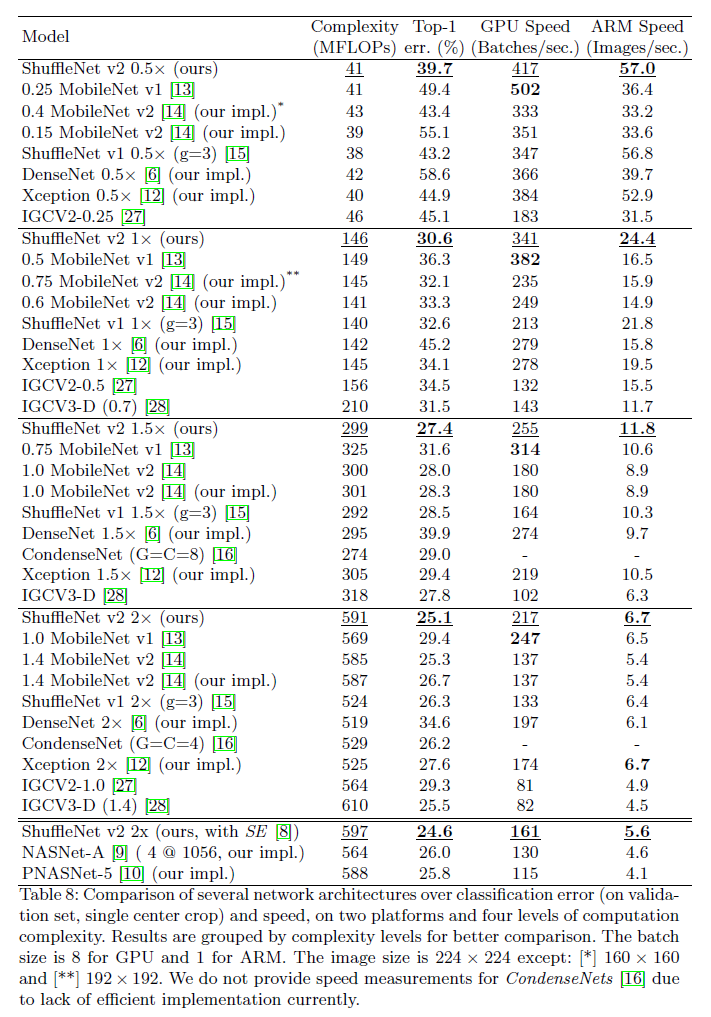
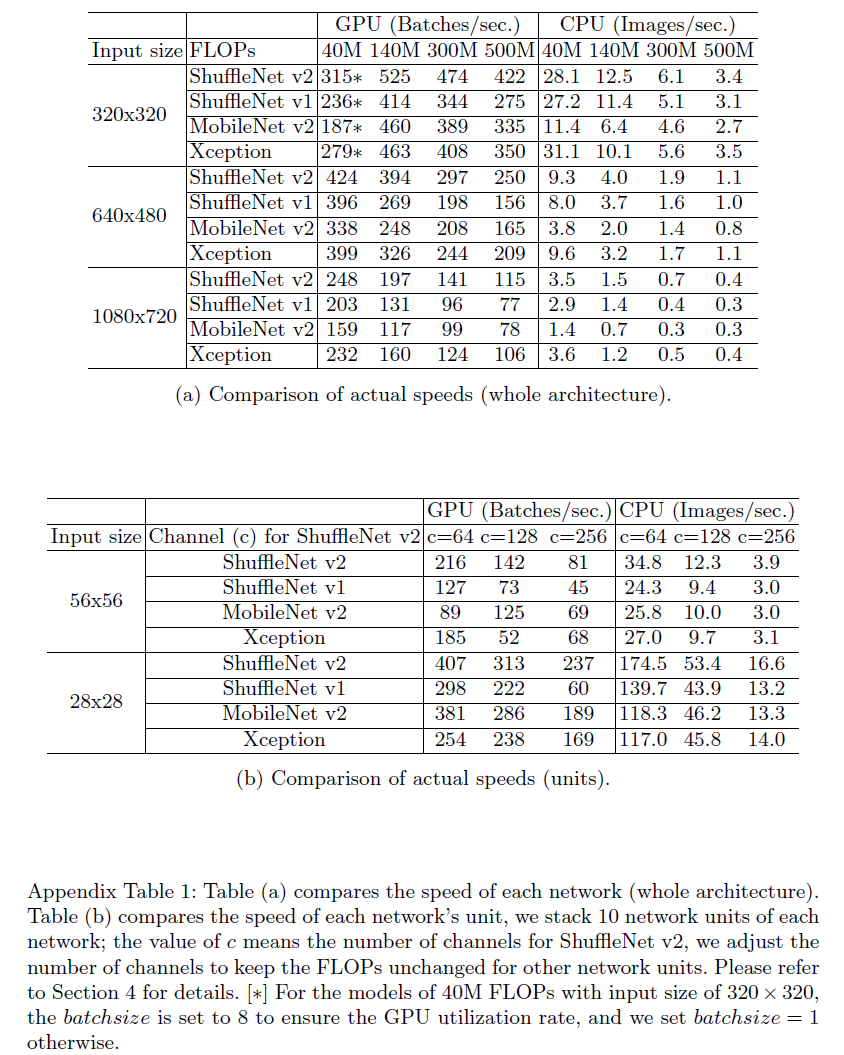
表8中提到的ShuffleNet v2 with SE/residual的结构如下所示:
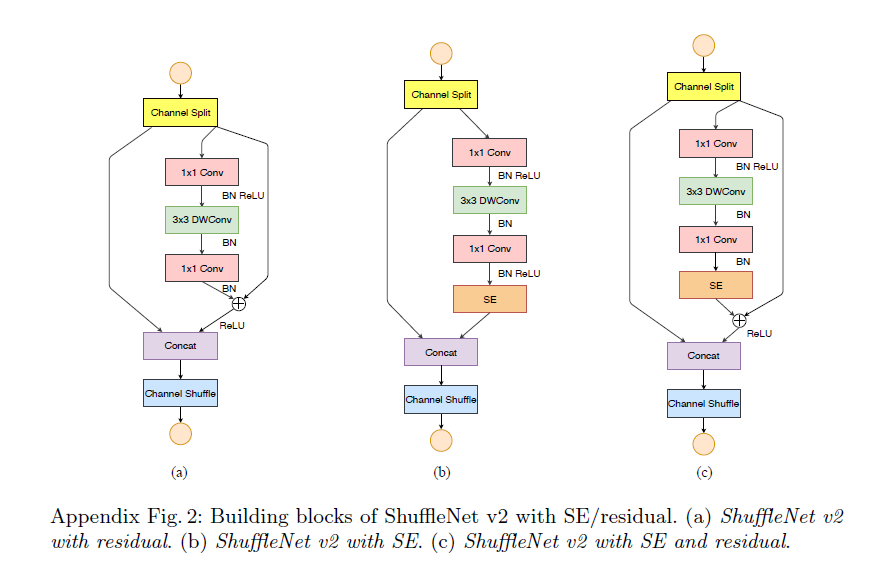
SE block的讲解见:【论文阅读】Squeeze-and-Excitation Networks。

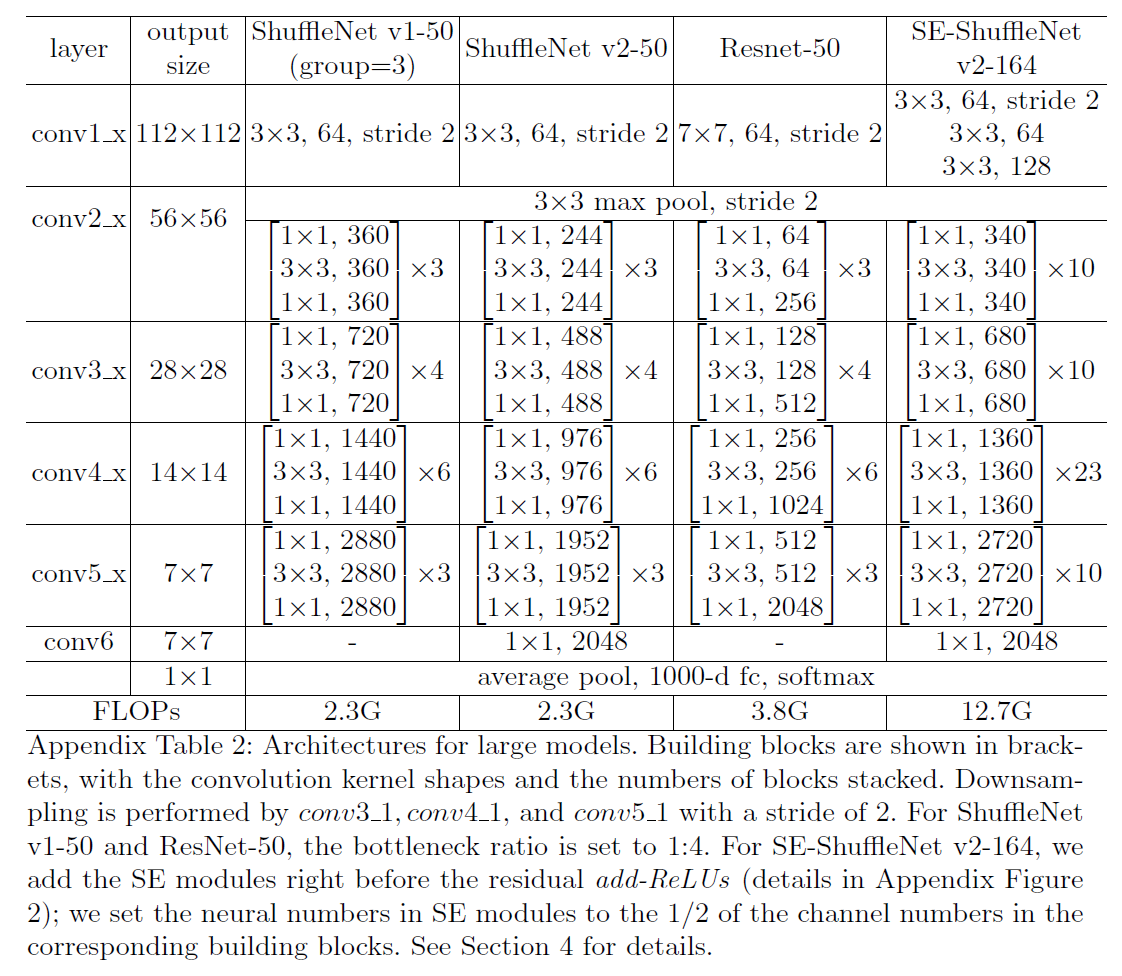
其中,SE-ShuffleNet v2-164的网络结构见下:
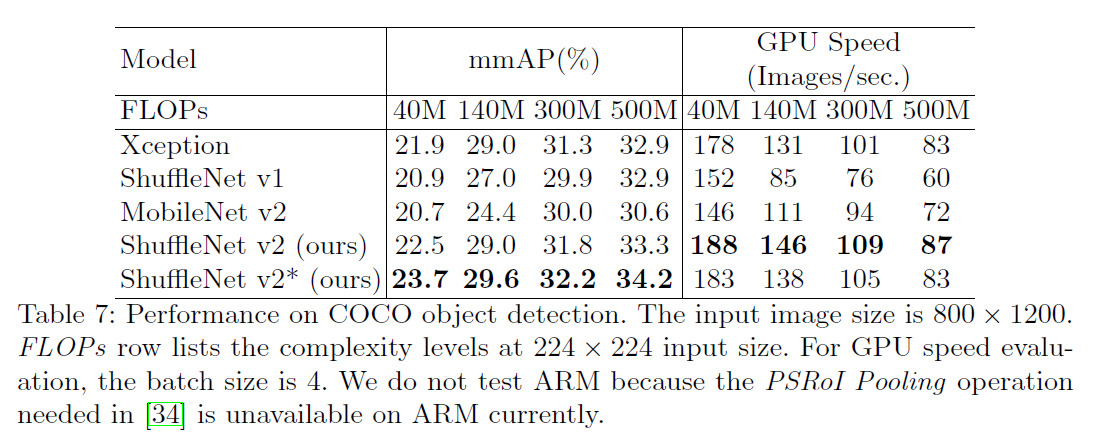
在目标检测任务上的表现:
5.Conclusion
不再赘述。
6.原文链接
👽ShuffleNet V2:Practical Guidelines for Efficient CNN Architecture Design