本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.极限的定义
极限:$\lim_{x \to x_0} f(x)=L$,表示函数$f(x)$在$x_0$处的极限为$L$。
2.无穷小和无穷小的阶数
无穷小的定义:若$x\to x_0$(或$x\to\infty$)时,函数$f(x)\to 0$,则称函数$f(x)$为$x\to x_0$时的无穷小。
2.1.无穷小的阶数
无穷小量是以0为极限的函数,而不同的无穷小量收敛于0的速度有快有慢。因此两个无穷小量之间又分为:
- 高阶无穷小量
- 低阶无穷小量
- 同阶无穷小量
- 等价无穷小量
首先规定$f,g$都为$x\to x_0$(也可以是$x\to \infty$)时的⚠️无穷小⚠️,$g$在某$x_0$的空心邻域恒不为0。
2.1.1.高低阶无穷小量
$\lim_{x\to x_0}\frac{f(x)}{g(x)}=0$,则称当$x\to x_0$时,$f$为$g$的高阶无穷小量,或称$g$为$f$的低阶无穷小量。
记作$f(x)=o(g(x))(x\to x_0)$。
2.1.2.同阶无穷小量
当$\lim_{x\to x_0}\frac{f(x)}{g(x)}=c(c\neq0)$时,$f$和$g$为$x\to x_0$的同阶无穷小量。
例如:当$x\to 0$时的同阶无穷小量:$1-\cos x$与$\frac{1}{2}x^2$;$\tan x-x$与$\frac{x^3}{3}$。
2.1.3.等价无穷小量
$\lim_{x\to x_0}\frac{f(x)}{g(x)}=1$,则称$f$和$g$是当$x\to x_0$时的等价无穷小量,记作:$f(x)\sim g(x)(x\to x_0)$。
等价无穷小量应用最为广泛,常见的有:
当$x\to 0$时:$\sin x \sim x$,$\tan x \sim x$,$\ln (1+x)\sim x$。
2.1.4.$k$阶无穷小
$\lim_{x\to x_0}\frac{f(x)}{[g(x)]^k}=c\neq 0,k>0$,称$f(x)$是关于$g(x)$的$k$阶无穷小。
3.无穷大和无穷大的阶数
无穷大的定义:当$x\to x_0$时,$\lim_{x\to x_0}f(x)=\infty$,或者是$\lim_{x\to \infty}f(x)=\infty$。
3.1.无穷大的阶数
⚠️前提:设当$x\to x_0$(或$x\to \infty$)时,$f(x),g(x)$都为无穷大量。
- 若$\lim_{x\to x_0}\frac{f(x)}{g(x)}=\infty$,则称当$x\to x_0$时,$f(x)$为$g(x)$的高阶无穷大(⚠️没有低阶无穷大的说法!)。
- 若$\lim_{x\to x_0}\frac{f(x)}{g(x)}=c\neq0$,则当$x\to x_0$时,$f(x)$与$g(x)$为同阶无穷大。
- 若$\lim_{x\to x_0}\frac{f(x)}{g(x)}=1$,则称当$x\to x_0$时,$f(x),g(x)$为等价无穷大量。
4.洛必达法则
洛必达法则:是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。
⚠️在运用洛必达法则之前,首先要完成两项任务:
- 分子分母的极限是否都等于零(或者无穷大)。
- 分子分母在限定的区域内是否分别可导。
如果这两个条件都满足,接着求导并判断求导之后的极限是否存在:
- 如果存在,直接得到答案。
- 如果不存在,则说明此种未定式不可用洛必达法则来解决。
- 如果不确定,即结果仍然为未定式,再在验证的基础上继续使用洛必达法则。
5.极限不存在的情况
极限不存在的情况:
- 极限为无穷大时,极限不存在。(但是,我们常常还是写成$\lim f(x)=\infty$,即使这样写,还是不存在。)
- 左右极限不相等,包括三种情况:
- 一侧有极限,一侧没有。
- 两侧都没有。
- 两侧都有,但不相等
5.1.左右极限
关于左右极限:当从不同方向趋近$x_0$时,就产生了左右极限。例如:
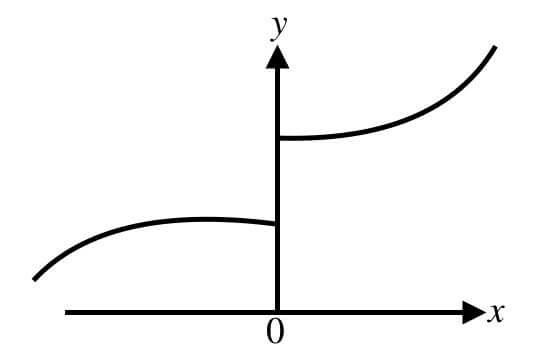
举个左右极限不相等的例子,例如有分段函数,当$x\to 0$时,左右极限不相等:
 ⚠️不是分段函数也可能出现这种情况,如$f(x)=\frac{\mid x \mid}{x}$,有:
⚠️不是分段函数也可能出现这种情况,如$f(x)=\frac{\mid x \mid}{x}$,有:
- $\lim_{x\to 0^-}f(x)=-1$
- $\lim_{x\to 0^+}f(x)=1$
5.2.极限为无穷小时,极限是否存在?
分4种情况:
- 结果若是无穷小,无穷小就用0代入,0也是极限,此时极限存在。
- 若是分子的极限是无穷小,分母的极限不是无穷小,答案就是0,整体极限存在。
- 如果分子的极限不是无穷小,而分母的极限是无穷小,答案不是正无穷大,就是负无穷大,整体的极限不存在。
- 若分子分母各自的极限都是无穷小,那就必须用洛必达法则确定最后的结果。
6.夹逼定理
学习完极限的一些知识后,现在介绍一个有关极限的非常重要的定理,叫做夹逼定理,也叫两边夹定理:
当$x\in U(x_0,r)$时,有$g(x)\leqslant f(x)\leqslant h(x)$成立,并且$\lim_{x\to x_0}g(x)=A,\lim_{x\to x_0}h(x)=A$,那么
\[\lim_{x\to x_0}f(x)=A\]7.重要极限
- $\lim_{x\to 0} \frac{\sin (x)}{x}=1$(不能用洛必达法则证明该公式!)
- $\lim_{x\to \infty} \frac{x^\alpha}{e^x}=0$(对于任意正数$\alpha$)
- $\lim_{x\to \infty} \frac{\ln {x}}{x^\alpha}=0$(对于任意正数$\alpha$)
- $\lim_{x\to \infty} (1+\frac{1}{x})^x=e$