本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.矩阵的基本概念
在数学中,矩阵(matrix)是一个按照长方阵列排列的复数或实数集合。通常使用小括号包裹起来(有的地方会使用中括号)。
由$m\times n$个数$a_{ij}$排成的m行n列的矩阵,简称$m\times n$矩阵。记作:
\[A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix}\]这$m\times n$个数称为矩阵A的元素,简称为元,数$a_{ij}$位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数$a_{ij}$为(i,j)元的矩阵可记为$(a_{ij})$或$(a_{ij})_{m\times n}$,$m\times n$矩阵A也记作$A_{mn}$。
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵。
1.1.矩阵的迹(trace)
在线性代数中,一个$n\times n$矩阵A的主对角线上各元素的总和被称为矩阵A的迹(或迹数),一般记为$tr(A)$。
1.2.矩阵的秩(rank)
在线性代数中,一个矩阵A的列秩是A的线性独立的纵列的极大数目。类似的,行秩是A的线性无关的横行的极大数目。
矩阵的列秩和行秩总是相等的,因此它们可以简单地称作矩阵A的秩。通常表示为$r(A),rank(A)$或$rk(A)$。
2.矩阵类型
矩阵有很多特殊的类型,这里仅介绍几种常见的类型。
2.1.同型矩阵
如果这两个或者两个以上的矩阵的行数和列数都相同,那么就说这两个或两个以上的矩阵是同型矩阵。
2.2.方阵
行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。
2.3.单位矩阵
在矩阵乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1,除此以外全都为0。即:
\[\begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{pmatrix}\]⚠️任何矩阵与单位矩阵相乘都等于本身。
单位矩阵通常用E表示。
2.4.转置矩阵
将矩阵的行列互换得到的新矩阵称为转置矩阵。例如矩阵A的转置矩阵(记为$A^T$)为:
\[\begin{pmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \\ \end{pmatrix}\]有定义可知,A为$m\times n$矩阵,则$A^T$为$n\times m$矩阵。
⚠️转置矩阵的行列式不变。
👉运算性质:
- $(A^T)^T=A$
- $(A+B)^T=A^T+B^T$
- $(kA)^T=kA^T$
- $(AB)^T=B^TA^T$
- $\det (A^T)=\det(A)$
2.5.对称矩阵和反对称矩阵
如果n阶方阵和它的转置相等,即$A^T=A$,则称矩阵A为对称矩阵。
如果$A^T=-A$,则称矩阵A为反对称矩阵。
2.6.伴随矩阵
设矩阵$A=(a_{ij})_{n\times n}$,将矩阵A的元素$a_{ij}$所在的第i行第j列元素划去后,剩余的$(n-1)^2$,各元素按原来的排列顺序组成的n-1阶矩阵所确定的行列式称为元素$a_{ij}$的【余子式】,记为$M_{ij}$,称$A_{ij}=(-1)^{i+j}M_{ij}$为元素$a_{ij}$的【代数余子式】。
- $a_{ij}$ 为矩阵A的元素/元。
- $M_{ij}$为元素$a_{ij}$的余子式
- $A_{ij}$为元素$a_{ij}$的代数余子式
方阵$A=(a_{ij})_{n\times n}$的各元素的代数余子式$A_{ij}$所构成的如下矩阵$A^*$:
\[\begin{pmatrix} A_{11} & A_{21} & \cdots & A_{n1} \\ A_{12} & A_{22} & \cdots & A_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ A_{1n} & A_{2n} & \cdots & A_{nn} \\ \end{pmatrix}\]该矩阵$A^*$称为矩阵A的伴随矩阵。
2.7.逆矩阵
设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶方阵B,使得:$AB=BA=E$。则我们称B是A的逆矩阵,而A则被称为可逆矩阵。(E为单位矩阵。)
A的逆矩阵记为$A^{-1}$。
👉逆矩阵的性质:
- 可逆矩阵一定是方阵。
- 如果矩阵A是可逆的,其逆矩阵是唯一的。
- A的逆矩阵的逆矩阵还是A,记作$(A^{-1})^{-1}=A$。
- 可逆矩阵A的转置矩阵$A^T$也可逆,并且$(A^T)^{-1}=(A^{-1})^T$。
- 若矩阵A可逆,则矩阵A满足消去率:
- AB=0(或BA=0),则B=0。
- AB=AC(或BA=CA),则B=C。
- 两个可逆矩阵的乘积依然可逆。
- 矩阵可逆当且仅当它是满秩矩阵。
关于性质5:
矩阵乘积一般不满足消去率,即已知AB=0,一般推不出A=0(或B=0);或者说,已知AX=AY一般推不出X=Y。例如:
$\begin{pmatrix} 1 & 0 \\ 0 & 0 \\ 3 & 0 \ \end{pmatrix}\times \begin{pmatrix} 2 \\ 1 \ \end{pmatrix}=\begin{pmatrix} 2 \\ 0 \\ 6 \ \end{pmatrix}$
$\begin{pmatrix} 1 & 0 \\ 0 & 0 \\ 3 & 0 \ \end{pmatrix}\times \begin{pmatrix} 2 \\ 3 \ \end{pmatrix}=\begin{pmatrix} 2 \\ 0 \\ 6 \ \end{pmatrix}$
只有在矩阵可逆的情况下,才满足消去率。
2.8.满秩矩阵
设A是n阶矩阵(方阵),若$r(A)=n$,则称A为满秩矩阵。
❗️但满秩不局限于n阶方阵:
- 若矩阵秩等于行数,称为行满秩。
- 若矩阵秩等于列数,称为列满秩。
2.9.正定矩阵、半正定矩阵、负定矩阵、半负定矩阵
设A是n阶方阵,若对于每个非零实向量X,都有:
- $X^TAX\geqslant 0$,就称A为半正定矩阵。
- $X^TAX>0$,就称A为正定矩阵。
- $X^TAX\leqslant 0$,就称A为半负定矩阵。
- $X^TAX<0$,就称A为负定矩阵。
如果一个埃尔米特矩阵既不是半正定也不是半负定的,那么称其为不定矩阵。
3.矩阵的运算
3.1.加减乘除
3.1.1.矩阵加法
⚠️只有同型矩阵之间才可以进行加法。
\[\begin{pmatrix} 1 & 4 & 2 \\ 2 & 0 & 0 \\ \end{pmatrix} + \begin{pmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ \end{pmatrix}=\begin{pmatrix} 1+0 & 4+0 & 2+5 \\ 2+7 & 0+5 & 0+0 \\ \end{pmatrix}=\begin{pmatrix} 1 & 4 & 7 \\ 9 & 5 & 0 \\ \end{pmatrix}\]3.1.2.矩阵减法
⚠️只有同型矩阵之间才可以进行减法。
\[\begin{pmatrix} 1 & 4 & 2 \\ 2 & 0 & 0 \\ \end{pmatrix} - \begin{pmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ \end{pmatrix}=\begin{pmatrix} 1-0 & 4-0 & 2-5 \\ 2-7 & 0-5 & 0-0 \\ \end{pmatrix}=\begin{pmatrix} 1 & 4 & -3 \\ -5 & -5 & 0 \\ \end{pmatrix}\]3.1.3.矩阵乘法
3.1.3.1.与数相乘
\[\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{pmatrix}\times 3 = \begin{pmatrix} 3 & 6 & 9 \\ 12 & 15 & 18 \\ \end{pmatrix}\]3.1.3.2.与矩阵相乘
两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是$m\times n$矩阵和B是$n\times p$矩阵,它们的乘积C是一个$m\times p$矩阵$C=(c_{ij})$,记作$C=AB$。例如:
\[\begin{pmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \\ \end{pmatrix}\times \begin{pmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \\ \end{pmatrix}=\begin{pmatrix} (1\times 3+0\times 2 +2\times 1) & (1\times 1+0\times 1+2\times 0) \\ (-1\times 3+3\times 2+1\times 1) & (-1\times 1+3\times 1+1\times 0) \\ \end{pmatrix}=\begin{pmatrix} 5 & 1 \\ 4 & 2 \\\end{pmatrix}\]3.1.4.矩阵除法
实际上并不存在矩阵除法,所谓的矩阵除法其实是乘上其逆矩阵。
若A和B是维数相同的两个方阵,且B为可逆矩阵,则矩阵A除以矩阵B相当于是矩阵B的逆矩阵乘上矩阵A:
\[A/B=B^{-1}A\]⚠️因为矩阵乘法并没有交换律,所以通常有$B^{-1}A\neq AB^{-1}$。
3.2.行列式
行列式在数学中,是一个函数,其定义域为det的矩阵A,取值为一个标量,写作det(A)或$\mid A\mid$(即矩阵A的模)。
⚠️行列式仅存在于方阵,称为n阶行列式。
假设方阵A为:
\[\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{pmatrix}\] \[\det(A)=\mid A \mid=\sum_{p_1,p_2,\cdots ,p_n} (-1)^{\mathcal{T}(p_1,p_2,\cdots ,p_n)}a_{1p_1}a_{2p_2}\cdots a_{np_n}\]其中$p_1,p_2,\cdots ,p_n$为n个自然数$1,2,\cdots ,n$的某一排列,$\mathcal{T}(p_1,p_2,\cdots ,p_n)$为排列$p_1,p_2,\cdots ,p_n$的逆序数,$\sum_{p_1,p_2,\cdots ,p_n}$表示对$p_1,p_2,\cdots ,p_n$的所有排列求和。
逆序数:
举个例子:确定5级排列的逆序数。
在排列42531中,
- 4排在首位,前面没有比它大的数,故不构成逆序
- 2排在第二位,前面有一个数比它大,故构成一个逆序
- 5排在第三位,前面没有比它大的数,故不构成逆序
- 3排在第四位,前面有2个数比它大,故构成2个逆序
- 1排在第五位,前面有4个数比它大,故构成4个逆序
于是排列42531的逆序数为:$\mathcal{T}(42531)=0+1+0+2+4=7$
⚠️$\det(A)=\det(A^T)$
3.2.1.逆矩阵和行列式
\[A^{-1}=\frac{1}{\mid A \mid}A^*\]3.3.矩阵求导
矩阵求导有三种情况:
- 矩阵对标量求导
- 标量对矩阵求导
- 矩阵对矩阵求导
本文只讲解前两种情况。
3.3.1.矩阵对标量求导
矩阵$Y=(y_{ij})_{m\times n}$。
\[\frac{\partial \mathbf Y}{\partial x}=\begin{pmatrix} \frac{\partial y_{11}}{\partial x} & \frac{\partial y_{12}}{\partial x} & \cdots & \frac{\partial y_{1n}}{\partial x} \\ \frac{\partial y_{21}}{\partial x} & \frac{\partial y_{22}}{\partial x} & \cdots & \frac{\partial y_{2n}}{\partial x} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_{m1}}{\partial x} & \frac{\partial y_{m2}}{\partial x} & \cdots & \frac{\partial y_{mn}}{\partial x} \\ \end{pmatrix}\]3.3.2.标量对矩阵求导
矩阵$X=(x_{ij})_{p\times q}$。(⚠️注意:矩阵做了转置。)
\[\frac{\partial y}{\partial \mathbf X}=\begin{pmatrix} \frac{\partial y}{\partial x_{11}} & \frac{\partial y}{\partial x_{21}} & \cdots & \frac{\partial y}{\partial x_{p1}} \\ \frac{\partial y}{\partial x_{12}} & \frac{\partial y}{\partial x_{22}} & \cdots & \frac{\partial y}{\partial x_{p2}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y}{\partial x_{1q}} & \frac{\partial y}{\partial x_{2q}} & \cdots & \frac{\partial y}{\partial x_{pq}} \\ \end{pmatrix}\]4.向量的定义
向量也称为矢量,指具有大小和方向的量。
👉坐标表示:
\[\vec{a}=(x_0,y_0)\]👉矩阵表示($n\times 1$):
\[\mathbf a=\begin{pmatrix} x_0 \\ y_0 \\ \end{pmatrix}\]5.向量相关定义
5.1.向量的模
向量的大小,也就是向量的长度(或称模)。
向量$\mathbf a$的模记作$\mid \mathbf a \mid$。
若向量$\vec a=(x,y)$,则$\mid \vec a \mid=\sqrt{x^2+y^2}$。
⚠️因为方向不能比较大小,所以向量也就不能比较大小。
5.2.单位向量
长度为一个单位(即模为1)的向量,叫做单位向量。与$\mathbf a$同向,且长度为单位1的向量,叫做$\mathbf a$方向上的单位向量。
5.3.负向量
如果向量AB与向量CD的模相等且方向相反,那么把向量AB叫做向量CD的负向量,也称为相反向量。
5.4.零向量
长度为0的向量叫做零向量,记作$\mathbf 0$。
零向量的始点和终点重合,所以零向量没有确定的方向,或说零向量的方向是任意的。
5.5.相等向量
长度相等且方向相同的向量叫做相等向量。可记作$\mathbf a=\mathbf b$。
⚠️所有的零向量都相等。
5.6.位置向量
对于坐标平面内的任意一点P,我们把向量OP叫做点P的位置向量,其中O点为坐标原点。
5.7.方向向量
直线l上的向量$\mathbf a$以及与向量$\mathbf a$共线的向量叫做直线l上的方向向量。
5.8.平行向量
方向相同或相反的非零向量叫做平行(或共线)向量。可记作$\mathbf a // \mathbf b$。
⚠️零向量与任一向量平行。
5.9.法向量
直线l垂直于平面$\alpha$,取直线l的方向向量$\mathbf a$,则向量$\mathbf a$叫做平面$\alpha$的法向量。
6.向量的基本运算
设$\mathbf a=(m_1,m_2,\cdots,m_k);\mathbf b=(n_1,n_2,\cdots,n_k)$。
6.1.向量加法
\[\mathbf a+\mathbf b=(m_1+n_1,m_2+n_2,\cdots,m_k+n_k)\]向量加法的几何意义见下图(平行四边形法则):
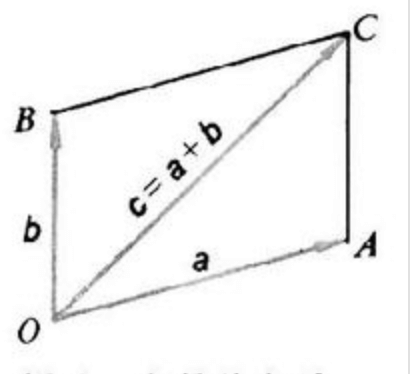
6.2.向量减法
\[\mathbf a-\mathbf b=(m_1-n_1,m_2-n_2,\cdots,m_k-n_k)\]向量减法的几何意义见下图(三角形法则):
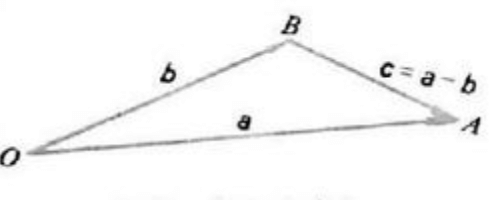
6.3.数乘
有实数$\lambda$:
\[\lambda \mathbf a=(\lambda m_1,\lambda m_2,\cdots,\lambda m_k)\]- 当$\lambda > 0$时,$\lambda \mathbf a$的方向与$\mathbf a$的方向相同。
- 当$\lambda < 0$时,$\lambda \mathbf a$的方向与$\mathbf a$的方向相反。
- 当$\lambda = 0$时,$\lambda \mathbf a=\mathbf 0$,方向任意。
6.4.数量积
向量的数量积又称内积、点积(❗️得到的是一个数值):
\[\mathbf a \cdot \mathbf b=m_1n_1+m_2n_2+\cdots+m_kn_k\]几何意义(⚠️只对二维和三维空间有效):
\[\vec a \cdot \vec b=\mid \vec a \mid \mid \vec b \mid \cos \theta\]6.5.向量积
向量的向量积又称外积、叉积(❗️得到的是一个向量)。记作$\mathbf a \times \mathbf b$,这里的“$\times$”并不是乘号,只是一种表示方法,与“$\cdot$”不同,也可记作“$\wedge$”。向量积具体的计算方法本文不再详述。