【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.符号约定
在正式开始接触深度学习之前,首先约定一些数学符号,适用于整个【深度学习基础】系列博客。
用一对$(x,y)$表示一个单独的样本,其中$x\in \mathbb R^{n_x},y\in \{0,1 \}$。x是$n_x$维的特征向量(即有n个属性(或特征)),标签y为0或1(在二分类情况下)。
假设训练集共有m个样本,即$m_{train}$。训练集可表示为:
\[\{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)}) \}\]类似的,使用$m_{test}$表示测试集的样本数。
训练集的输入可表示为一个$n_x \times m_{train}$的矩阵,$X\in \mathbb R^{n_x \times m_{train}}$:
\[X=\begin{bmatrix} \vdots & \vdots & \vdots & \vdots \\ x^{(1)} & x^{(2)} & \vdots & x^{(m)} \\ \vdots & \vdots & \vdots & \vdots \end{bmatrix}\]每一个列向量代表一个样本。
同样的,训练集的标签可表示为一个$1\times m_{train}$的矩阵,$Y\in \mathbb R^{1\times m_{train}}$:
\[Y=\begin{bmatrix} y^{(1)},y^{(2)} ,...,y^{(m)}\end{bmatrix}\]2.基础知识
除了符号约定之外,还需要一些基础知识,可参考我之前的博客文章:
2.1.学习率
假设logistic回归中有参数$w,b$,其cost function为$J(w,b)$,在使用梯度下降法优化参数时有:$w:=w-\alpha \frac{ \partial J(w,b)}{\partial w},b:=b-\alpha \frac{ \partial J(w,b)}{\partial b}$,:=表示$w,b$的更新,式中$\alpha$即为学习率,决定了$w,b$朝梯度下降的方向走的步长。
3.计算图
接下来我们通过计算图(computation graph)简单了解下ANN中的正向和反向传播过程。
假设我们有cost function:$J(a,b,c)=3(a+bc)$,该函数可分为三个不同的步骤:
- $u=bc$
- $v=a+u$
- $J=3v$
把这三步画成如下的流程图:
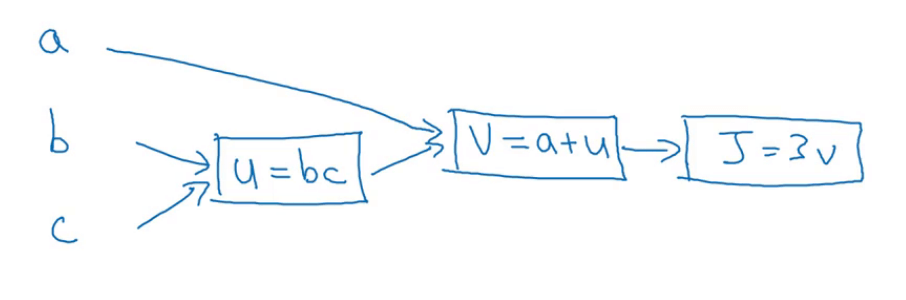
3.1.正向传播
假设现在有$a=5,b=3,c=2$,则我们按照计算图从左向右计算$J$的过程就是一个正向传播的过程:
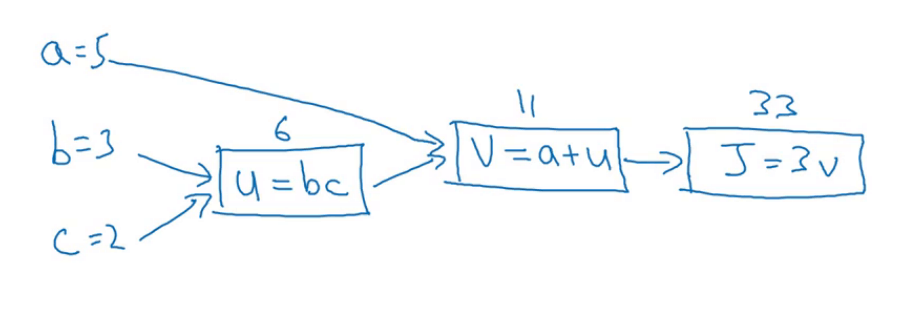
3.2.反向传播
那么接下来的任务就是优化cost function,如果我们采用梯度下降法的话,我们首先需要计算出在点(a=5,b=3,c=2)的梯度,即$[\frac{\partial J}{\partial a},\frac{\partial J}{\partial b},\frac{\partial J}{\partial c}]$,这个过程就是一个反向传播的过程:

可以看出,这个从右到左的反向传播过程其实就是链式法则求导的过程,例如:$\frac{dJ}{da}=\frac{dJ}{dv} \frac{dv}{da}=3\cdot 1=3$,可简化表示为$da=3$。
因为在反向传播求导数的过程中,分子都是$\partial J$(或者$d J$,两种表示方法是一个意思),因此在python代码中,我们通常使用$da,db,dc,du,dv$来简化表示$J$对其的偏导数。
4.梯度下降法在logistic回归中的应用
应用第3部分所讲的反向传播的内容,来看看梯度下降法在logistic回归中的实际应用。
4.1.一个样本
先来看下一个样本的简单情况。
\[z=w^T x+b\]预测该样本属于正样本的概率为($\sigma$为sigmoid联系函数):
\[\hat y=a=\sigma (z)=\frac{1}{1+e^{-z}}\]单样本的loss function为:
\[L(a,y)=-(y\log (a)+(1-y)\log (1-a))\]$log(a)$是以$e$为底的。
假设样本只有两个特征$x_1,x_2$。
构建计算图:
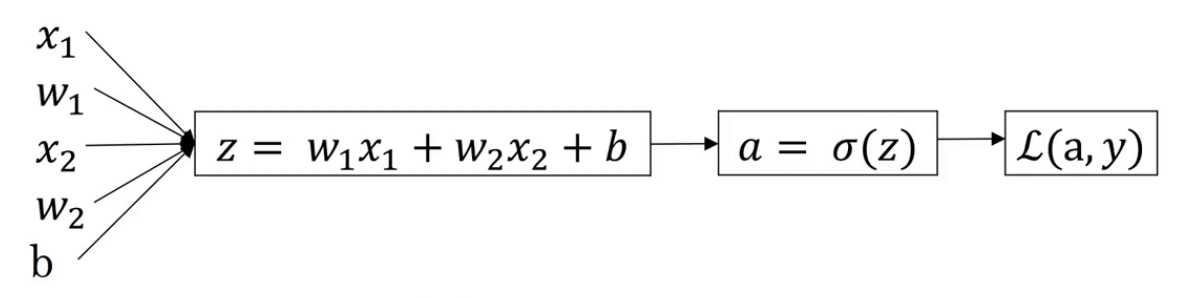
那么现在所需要做的就是优化$w_1,w_2,b$的值来最小化loss function $L(a,y)$。我们使用梯度下降法优化参数,首先需要通过后向传播计算其梯度:
- $\frac{d L(a,y)}{da}=-\frac{y}{a}+\frac{1-y}{1-a}$,代码中可简写为:$da=-\frac{y}{a}+\frac{1-y}{1-a}$。
- $\frac{d L(a,y)}{dz}=\frac{d L(a,y)}{da} \cdot \frac{da}{dz}=(-\frac{y}{a}+\frac{1-y}{1-a})\cdot [a(1-a)]=a-y$,代码中可简写为:$dz=a-y$。
- $\frac{d L(a,y)}{d w_1}=\frac{d L(a,y)}{da} \cdot \frac{da}{dz} \cdot \frac{dz}{dw_1}=x_1(a-y)$,代码中可简写为:$dw_1=x_1dz$。
- $\frac{d L(a,y)}{dw_2}=x_2(a-y)$,代码中可简写为:$dw_2=x_2dz$。
- $\frac{d L(a,y)}{db}=a-y$,代码中可简写为:$db=dz$。
$\frac{da}{dz}=(\frac{1}{1+e^{-z}})’=\frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}}=a(1-a)$
得到该点处的梯度$[dw_1,dw_2,db]$,然后配合学习率更新参数:
- $w_1:=w_1-\alpha \cdot dw_1$
- $w_2:=w_2-\alpha \cdot dw_2$
- $b:=b-\alpha \cdot db$
4.2.m个样本
接下来考虑更复杂的m个样本的情况。
m个样本的cost function为:
\[J(w,b)=\frac{1}{m} \sum^m_{i=1} L(a^{(i)},y^{(i)})\]其中,
\[a^{(i)}=\hat y ^{(i)}=\sigma (z^{(i)})=\sigma (w^T x^{(i)}+b)\]此时求其全局梯度(以$w_1$为例):
$\frac{\partial}{\partial w_1} J(w,b)=\frac{1}{m}\sum^m_{i=1} \frac{\partial}{\partial w_1}L(a^{(i)},y^{(i)})=\frac{1}{m}\sum^m_{i=1} dw_1$
可以看出,全局梯度就是单样本的梯度的算术平均数。
因此我们可使用以下伪代码求全局cost和全局梯度:
- $J=0;dw_1=0;dw_2=0;db=0;$
- for i=1 to m
- $z^{(i)}=w^Tx^{(i)}+b$
- $a^{(i)}=\sigma (z^{(i)})$
- $J+=-[y^{(i)}\log a^{(i)}+(1-y^{(i)})\log (1-a^{(i)})]$
- $dz^{(i)}=a^{(i)}-y^{(i)}$
- for j=1 to n
- $dw_j+=x_j^{(i)} dz^{(i)}$
- $db+=dz^{(i)}$
- $J/=m;$
- $dw_1/=m;dw_2/=m;db/=m;$
但是上述代码有两个for循环,第一个for循环是循环所有的样本,第二个for循环是循环所有的特征。深度学习算法中,在代码中显式的使用for循环会使算法很低效。而下节课要讲的向量化(vectorization)技术可以帮助我们的代码摆脱这些显式的for循环,使我们的代码更为高效,更适合训练非常大的数据集。