【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.什么是深层神经网络?
深层(或者说深度)只是一个相对的概念。隐藏层越多的神经网络,其深度越深。
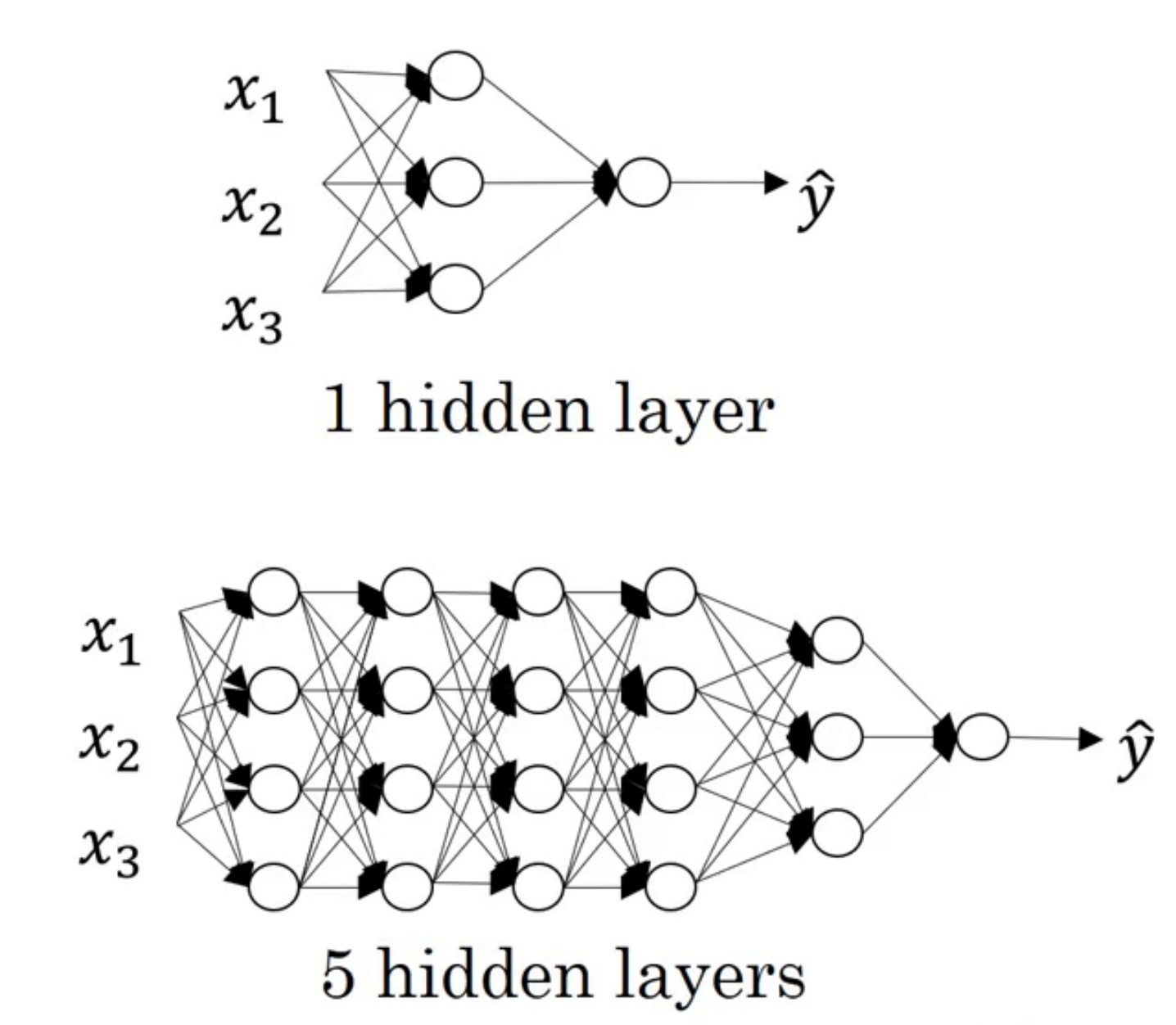
例如在上图中,含有5个隐层的神经网络就要比只含有1个隐层的神经网络要深。
有些函数只有非常深层的神经网络能够学习,而浅一些的模型通常无法学习。
2.符号约定
之前“深度学习基础”系列博客中所用的其他符号约定继续适用。在此基础,再添加一些新的符号:
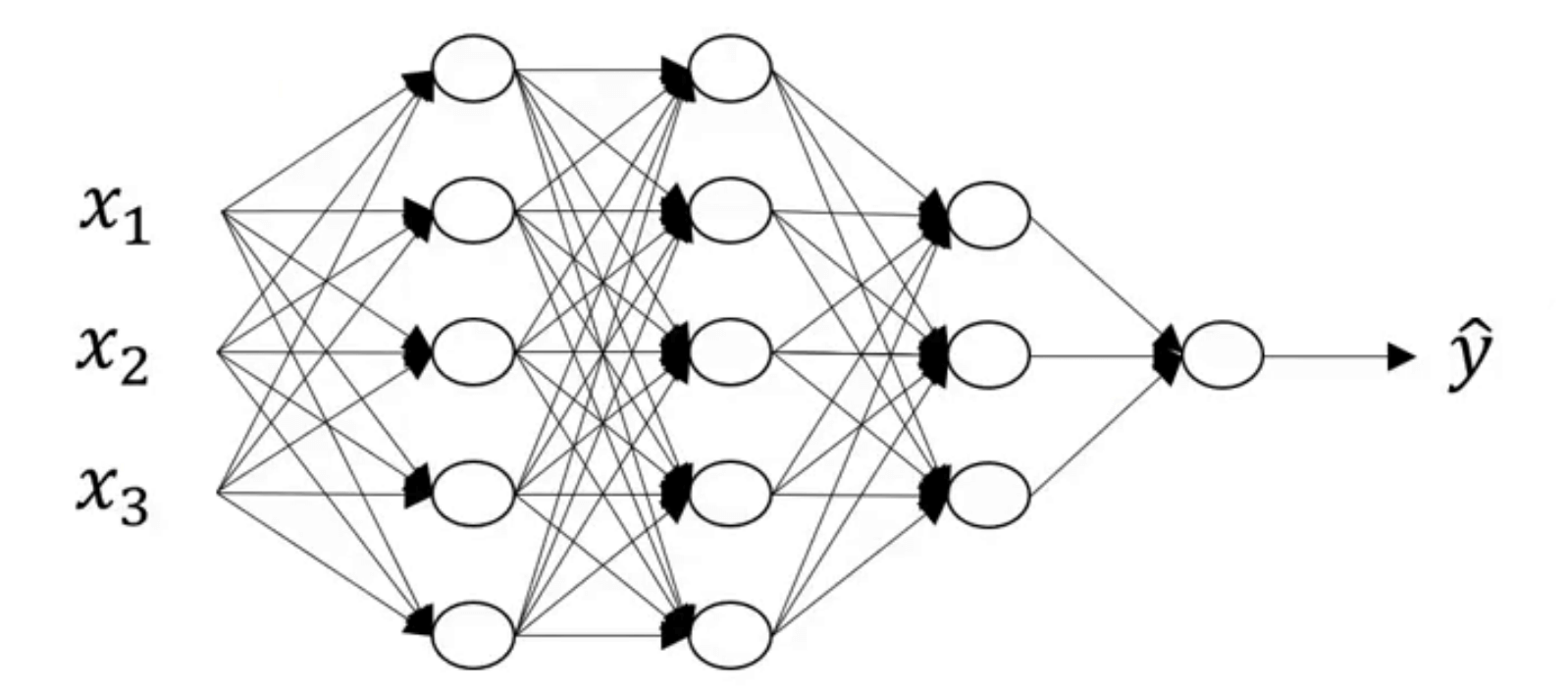
以上图中的4层神经网络为例。
关于神经网络层数的相关说明见【深度学习基础】第六课:浅层神经网络。
- 使用L表示神经网络的层数,例子中有L=4。
- 使用$n^{[l]}$表示第l层的神经元数量,例如本例中有:$n^{[0]}=3;n^{[1]}=n^{[2]}=5;n^{[3]}=3;n^{[4]}=1$。
- 使用$a^{[l]}$表示第l层激活函数的输出,即$a^{[l]}=g(z^{[l]})$。
3.深层神经网络的前向传播
深层神经网络的前向传播和其在浅层神经网络中是完全一样的。
依然以第2部分的4层神经网络为例。
👉首先考虑只有一个样本的情况:
- $z^{[1]}=w^{[1]}x+b^{[1]}$,也可以写为$z^{[1]}=w^{[1]}a^{[0]}+b^{[1]}$
- $a^{[1]}=g^{[1]}(z^{[1]})$
- $z^{[2]}=w^{[2]}a^{[1]}+b^{[2]}$
- $a^{[2]}=g^{[2]}(z^{[2]})$
- $z^{[3]}=w^{[3]}a^{[2]}+b^{[3]}$
- $a^{[3]}=g^{[3]}(z^{[3]})$
- $z^{[4]}=w^{[4]}a^{[3]}+b^{[4]}$
- $a^{[4]}=g^{[4]}(z^{[4]})$
根据上述过程,我们可以总结出一个规律:
- $z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$
- $a^{[l]}=g^{[l]}(z^{[l]})$
👉针对多个样本的情况,我们一样可以得到:
- $Z^{[l]}=w^{[l]}A^{[l-1]}+b^{[l]}$
- $A^{[l]}=g^{[l]}(Z^{[l]})$
❗️在算法实际实现时,这里不可避免的需要使用一个显式的for循环来依次计算各个层。
4.深层神经网络的反向传播
深层神经网络的反向传播过程和浅层神经网络是一样的,详细推导可见【深度学习基础】第八课:神经网络的梯度下降法。我们可以很容易的总结出规律:
👉单个样本时:
- $dz^{[l]}=da^{[l]}*g^{[l]’}(z^{[l]})$
- $dw^{[l]}=dz^{[l]}a^{[l-1]}$
- $db^{[l]}=dz^{[l]}$
- $da^{[l-1]}=w^{[l]^T}dz^{[l]}$
👉多个样本时:
- $dZ^{[l]}=dA^{[l]}*g^{[l]’}(Z^{[l]})$
- $dw^{[l]}=\frac{1}{m}dZ^{[l]}A^{[l-1]^T}$
- $db^{[l]}=\frac{1}{m} np.sum(dZ^{[l]},axis=1,keepdims=True)$
- $dA^{[l-1]}=w^{[l]^T}dZ^{[l]}$
5.核对矩阵的维数
在代码实现深层神经网络时,核对矩阵维数是一个有效降低算法bug的方法。
以一个5层神经网络为例:
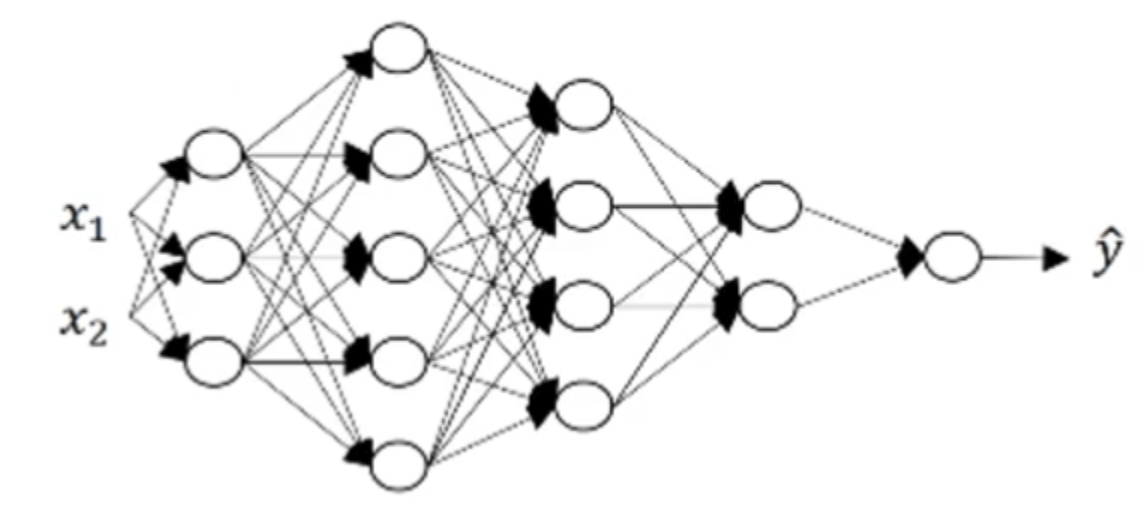
👉一个样本的情况:
- $z^{[1]}=w^{[1]}a^{[0]}+b^{[1]}$
- 矩阵维数:$(3\times 1)=(3\times 2)(2\times 1)+(3\times 1)$,即$(n^{[1]}\times 1)=(n^{[1]}\times n^{[0]})(n^{[0]}\times 1)+(n^{[1]}\times 1)$。
后续层数基本类似,这里就不再赘述。可以得到规律:$w^{[l]}$的维度通常为$(n^{[l]},n^{[l-1]})$,$b^{[l]}$的维度通常为$(n^{[l]},1)$。
此外,在反向传播过程中,dw的维度和w相同,db的维度和b相同。
👉多个样本的情况(共m个样本):
- $Z^{[1]}=w^{[1]}A^{[0]}+b^{[1]}$
- 矩阵维数:$(3\times m)=(3\times 2)(2\times m)+(3\times 1)$,即$(n^{[1]}\times m)=(n^{[1]}\times n^{[0]})(n^{[0]} \times m)+(n^{[1]}\times 1)$。
其中w和b的维度和单样本时一样。可以总结出:Z和A的维度一样,均为$(n^{[l]},m)$。并且,在反向传播过程中,dZ、dA的维度和Z、A的维度也是一样的。
需要注意的一个细节是,这里b的维度仍然是$(n^{[l]}\times 1)$,而不是$(n^{[l]}\times m)$,是因为broadcasting会将b复制为一个$(n^{[l]}\times m)$的矩阵。
6.搭建深层神经网络
以下图中神经网络中的某一层l为例(用蓝色框圈出的部分):
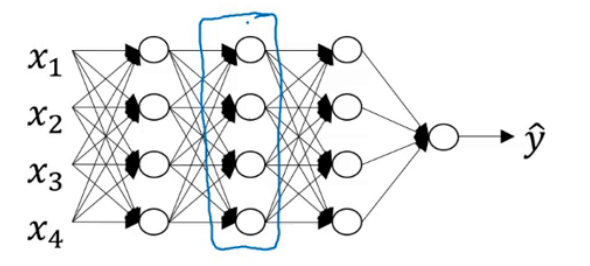
层l的正向传播和反向传播可表示为:
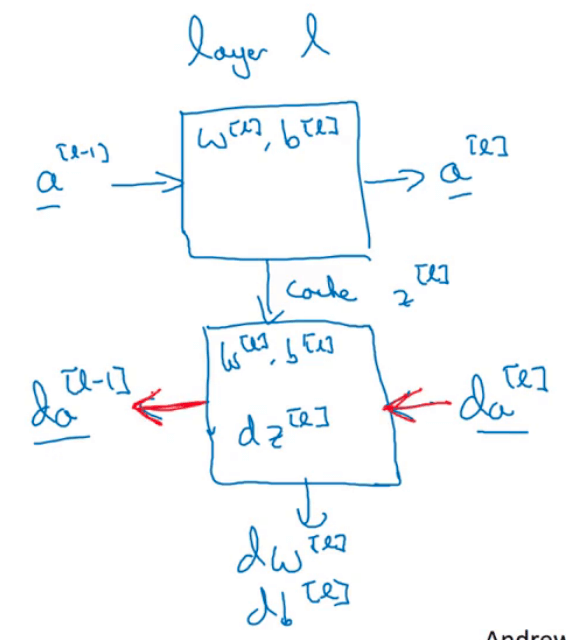
先看正向传播:
层l的输入为$a^{[l-1]}$,输出为$a^{[l]}$,从输入到输出需要$w^{[l]}$和$b^{[l]}$的参与。除此之外,将得到的中间变量$z^{[l]}$缓存起来,以供反向传播使用。
然后再来看反向传播(用红色箭头表示):
在反向传播过程中,层l的输入为$da^{[l]}$,输出为$da^{[l-1]}$。从输入到输出的过程需要$w^{[l]},b^{[l]},z^{[l]}$的参与。并且在此过程中可以输出中间变量:$dz^{[l]},dw^{[l]},db^{[l]}$。
现在我们已经明白了层l的正向和反向过程,那么将其扩展到整个网络:
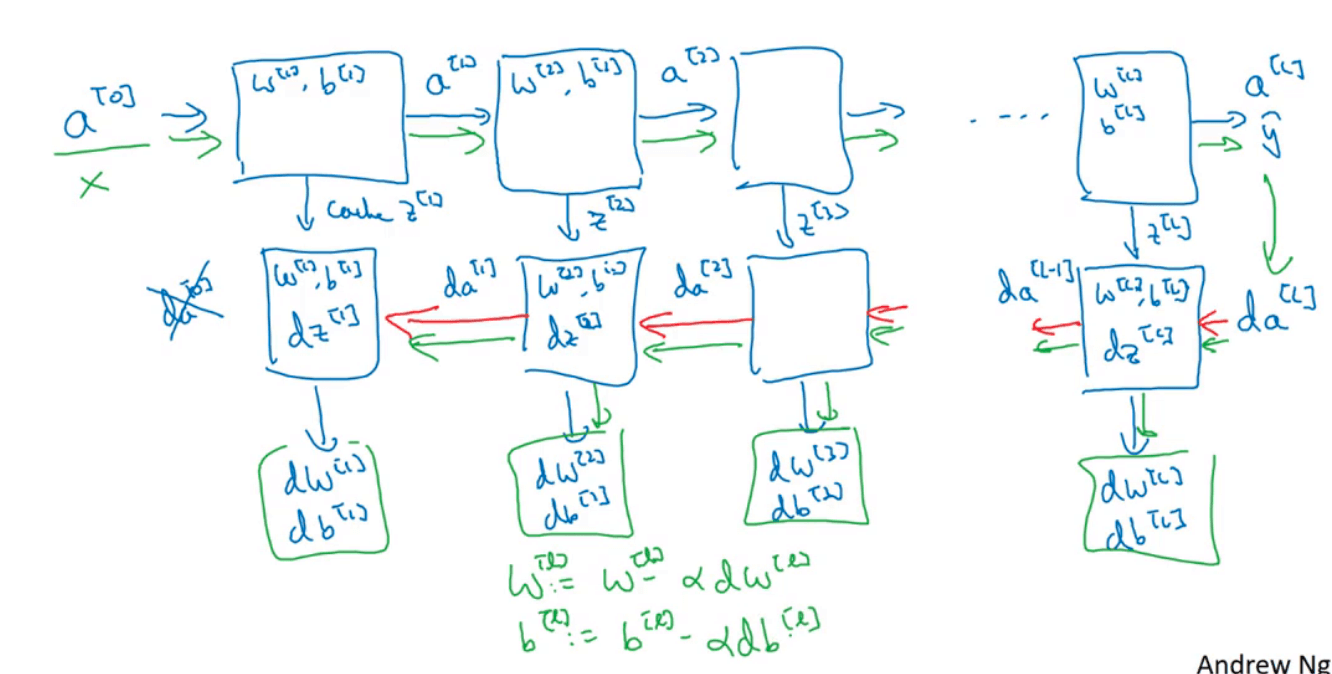
在代码实际实现正向传播的过程中,缓存z,w,b的值会方便反向传播的计算。
总结来说就是,在每一层中,有一个正向传播步骤以及对应的反向传播步骤,此外还有把信息从一步传递到另一步的缓存。
7.深层神经网络的超参数
目前为止,我们所了解到的深层神经网络中的超参数有:
- 学习率$\alpha$
- 梯度下降法的迭代次数
- 隐藏层的数量
- 每个隐藏层的神经元数
- 每层的激活函数
后续随着学习的深入,我们还会学到其他超参数,例如momentum、mini batch的大小、正则化参数等。
超参数的确定很大程度是基于已有的经验。后续的博客中,我们会用更系统的方法尝试各种超参数取值。
此外,电脑CPU或者GPU的更新换代、网络结构的变化、数据的变化,超参数的最优取值可能也会随之而变。所以需要时常检验结果,及时更新超参数的取值。