【深度学习基础】系列博客为学习Coursera上吴恩达深度学习课程所做的课程笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.什么是机器学习策略
假设我们有一个分类器,其正确率只有90%,并不能满足我们的需求。
根据之前【深度学习基础】系列博客中介绍的诸多方法,你可能会有很多想法去优化这个分类器,例如:
- 收集更多的训练数据。
- 增加训练数据的多样性。
- 训练更长的时间。
- 尝试另一种优化算法。
- 尝试规模更大或者更小的网络。
- 尝试dropout。
- 增加L2正则化。
- 修改网络结构,例如:
- 修改激活函数。
- 改变隐藏神经元的数目。
- ……
但是如果你选择了错误的优化方向,分类器的性能可能并无改善,甚至会越来越差。例如某个团队花了6个月的时间收集更多的训练数据,结果这些数据并没有改善模型的性能。
这时一个好的机器学习策略,可以使我们快速有效的判断哪些想法是靠谱的,是值得一试的,甚至提出新的想法,而哪些想法是可以放心舍弃的。
接下来我们通过上、下两篇博客介绍一些有用的机器学习策略。
2.正交化
2.1.什么是正交化
通过两个例子来简单说明什么是正交化。
👉例子一:
假设有一台老式电视机,有很多旋钮可以用来调整图像的各种性质。例如:
- 旋钮1:调整图像垂直方向的高度。
- 旋钮2:调整图像宽度。
- 旋钮3:调整图像的梯形角度。
- 旋钮4:调整图像的偏移量。
- 旋钮5:调整图像的旋转角度。
每个旋钮都有一个专有的功能,旋钮之间互不影响,这样我们就可以很容易调整图像到正确位置。但是如果有一个旋钮=0.1$\times$旋钮1+0.3$\times$旋钮2-0.7$\times$旋钮3+0.8$\times$旋钮4-0.7$\times$旋钮5,那么图像的多个性质会同时变化,这样几乎不可能把图像调整到正确位置。
让每个旋钮只负责调整图像的某一个性质,这就是正交化思想的运用。
👉例子二:
假设我们要开发一款赛车游戏,有三个按键分别用来操控汽车的方向、加速和刹车。如果我们只设计两个按键用来操控汽车:
- 按键1=0.3$\times$转向角度-0.8$\times$速度。
- 按键2=2$\times$转向角度+0.9$\times$速度。
从理论上来说,我们可以通过这两个按键将车子调整到我们希望的角度和速度。但这比分开控制方向、加速和刹车要困难的多。
2.2.正交化在机器学习中的应用
训练机器学习模型通常有以下四步:
- 优化其在训练集中的表现。
- 优化其在验证集中的表现。
- 优化其在测试集中的表现。
- 优化其在真实世界中的表现。
利用正交化的思想,针对不同的步骤给出一组特定的解决方法。
- 针对第一步,常用的方法有使用更大的网络、使用其他的优化算法等。
- 针对第二步,可以尝试加入正则化、增大训练集等。
- 针对第三步,可以扩大验证集。
- 针对第四步,尝试更改验证集或cost function。
因此我们可以对症下药,采用不同的策略去解决不同阶段出现的问题。并且尽可能的保证该策略只对该问题起作用而不影响其他性能。
3.模型评估指标
3.1.单一数字评估指标
如果我们设置一个单一数字作为模型的评估指标,那么我们可以很容易的判断出所用的优化策略使得模型的性能是变好了还是变差了,即我们的策略是否有效。
如下图所示,例如我们有分类器A,经过某一优化策略之后,得到了分类器B。从Precision的角度看,B的性能优于A,优化策略起到了积极作用;但是从Recall的角度看,A的性能优于B,优化策略并没有起到作用,反而降低了模型性能。

这时我们便需要一个单一数字指标来帮助我们快速的判断这两个分类器的优劣,例如我们可以选择F1值:

这样就可以很明显的看出分类器A的效果更好。
另一个简单的例子,多个分类器在不同的子数据集上的准确率各不相同,我们可以通过设置平均准确率这一单一数字评估指标来快速判断这几个分类器的优劣:

3.2.优化指标和满足指标
假设我们设置Accuracy为单一数字评估指标,如下图所示:

虽然分类器C的Accuracy要比A和B都高,但是其耗时过长,在实际应用中,我们可能更倾向于选择分类器B。
有两种方案来改善这种情况:
- 将单一数字评估指标设置为Accuracy和Running time的组合,例如设置为Accuracy-0.5$\times$Running time。
- 将Running time设置为满足指标,Accuracy为优化指标。即在Running time满足一定阈值的情况下(例如小于100ms),寻找最优的Accuracy。
通常我们会将N个指标中的某一个设置为优化指标,剩余N-1个设置为满足指标。
4.验证集和测试集
⚠️要保证验证集和测试集来自同一分布。
验证集和测试集的规模:【深度学习基础】第十课:神经网络模型的初步优化。
5.人的表现
5.1.人的表现和贝叶斯最优错误率
当一个机器学习模型的性能开始往人类水平努力时,进展是很快的。但过了一段时间,当这个算法表现比人类更好时,模型性能虽然仍会有提升,但是其提升的速度突然就变慢了。随着训练的推移,模型的性能始终无法超过某个理论上限。我们称这个上限为贝叶斯最优错误率(Bayes optimal error)。如下图所示:
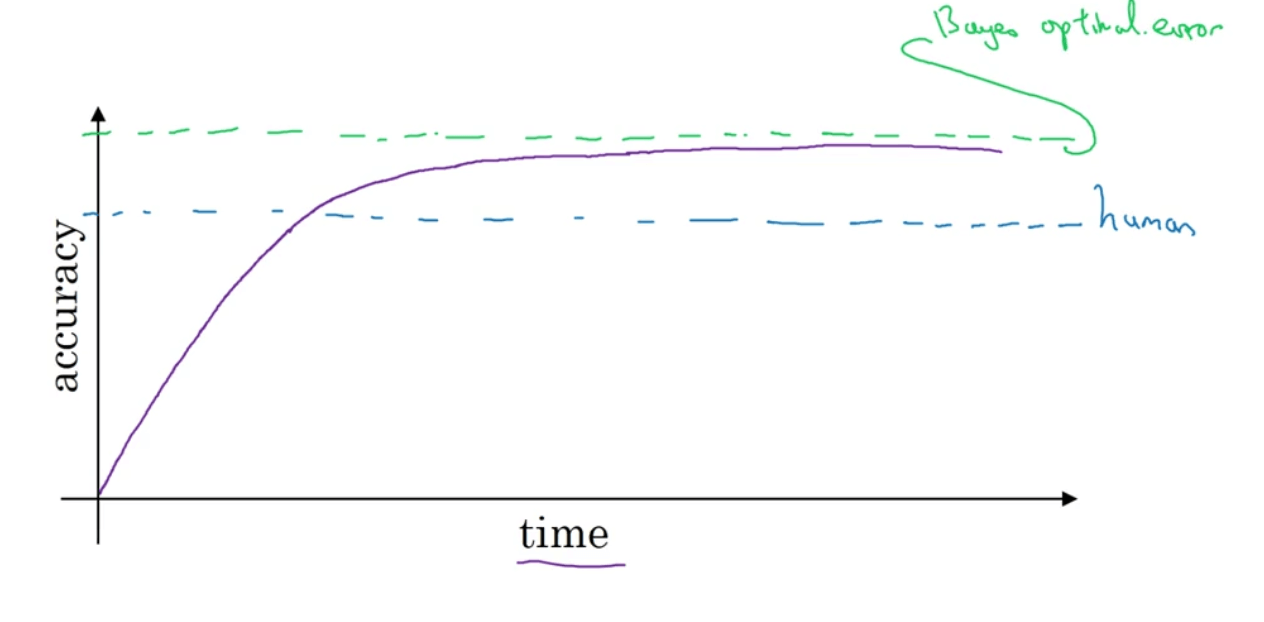
一般认为贝叶斯最优错误率是理论上可能达到的最优错误率。最优错误率一般不会为0,反过来说,最优准确率一般不是100%。举个例子来解释一下原因,比如对于语音识别任务,有一些音频就是很嘈杂,无论是人还是机器,通过任何技术都无法辨识出其所说的内容,又或者是图片分类任务,图片过于模糊以至于人和机器都无法正确识别。
模型优化的进程在其超过人类表现之后就缓慢下来,原因主要有两点:
- 当模型的性能不如人的表现时,我们可以根据人们自身的经验分析错误的原因并指导模型进行修正,其总能通过一些方法或者技术来有效的提高其性能,一旦模型性能超过人的表现,这些方法和技术就没那么好用了,我们就失去了优化的方向和指导。举个易懂的例子,当你的武功比你师傅还要高时,你的师傅已经没有什么可以教你的了。
- 人的表现在很多任务中接近于贝叶斯最优错误率。因此,当模型的性能超过人类表现时,已经没有太多的优化空间了。
5.2.可避免的偏差
假设我们用人的表现近似代替贝叶斯最优错误率。
以猫图片分类任务为例,假设人的错误率是1%,模型在训练集上的错误率是8%,在验证集上的错误率是10%。那么我们可以看出模型拟合的并不好,模型在训练集上的表现和人的表现差了7%,因此首先我们应该着眼于降低模型的偏差,例如训练更大的网络或者迭代时间更久一点。
保持模型在训练集和验证集上的错误率不变,假设人的错误率为7.5%。在这种情况下,模型已经拟合的相当不错了,我们应该专注于降低模型的方差,例如使用正则化或者扩大训练集。
当模型的性能超过人的表现时,我们不知道其距离贝叶斯最优错误率有多远,因此也无法判断是采用降低偏差的策略还是降低方差的策略,我们失去了优化的方向。这也是模型性能曲线在超过人的表现之后变得平缓的原因(对应5.1部分的原因1)。
因此在不同情况下,我们需要针对性的使用不同的优化策略。
通常将模型在训练集上的错误率与贝叶斯最优错误率之间的差距称为可避免的偏差。
模型在训练集上的错误率不可能小于贝叶斯最优错误率,除非出现了过拟合。
5.3.如何定义人的表现
以医学CT图像的分类任务为例,假设有:
- 没有医学背景的人的错误率为3%。
- 普通的放射科医生的错误率为1%。
- 经验丰富的放射科医生的错误率为0.7%。
- 经验丰富的放射科医生团队的错误率为0.5%。
那么这种情况下,我们该如何定义人的表现?在人类表现很好的领域(例如计算机视觉、自然语言处理等),我们通常用人的表现代替贝叶斯最优错误率,此时人的表现被定义为0.5%的错误率,即人类所能达到的最低错误率。但是从算法应用的层面上来讲,我们可能并不需要0.5%那么苛刻的条件,1%即可满足算法部署的要求,此时人的表现就可定义为1%的错误率。
因此,定义人的表现取决于我们的目的。如果我们只是希望我们的算法可以优于没有医学背景的人即可,那么人的表现就可以被定义为3%的错误率。