本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.共轭函数
共轭函数(conjugate function)亦称对偶函数:如果$f:\mathbb R^n \to \mathbb R$是一个函数,那么$f$的共轭函数:
\[f^*(y)=\sup \limits_{x \in dom \ f} (y^Tx-f(x))\]其中$f^*(y)$的定义域是使得等式右边有上界的那些$y$。
$x\in dom \ f$表示$x$在$f$的定义域内取值。
共轭函数的定义也可以写为(和上述定义等价):
\[f^*(t)=\max \limits_{x \in dom \ (f)} \{xt-f(x) \}\]共轭函数的性质:
- 共轭函数$f^*$是一个凸函数。
- 如果$g$是$f$的凸闭包,那么$g^{*}=f^{*}$。
- 对一般的函数$f$,$f^{**} \leqslant f$。
- 如果$f$是一个凸函数,那么$f^{**}=f$。
- Fenchel不等式(当$f$可微时亦称为Young不等式):$f(x)+f^*(y) \geqslant x^T y$。
- 如果$f$是凸函数而且可微,那么$f^{*}(y)=x^{* T} \nabla f(x^{*})-f(x^{*})$,其中$x^{*}$满足$\nabla f(x^{*})=y$。
- 如果$g(x)=f(Ax+b)$,则$g^{*}(y)=f^{*}(A^{-T}y)-b^TA^{-T}y$。
- 如果$f(u,v)=f_1(u)+f_2(v)$,那么$f^{*}(w,z)=f^{*}_1(w)+f^{*}_2(z)$。
性质证明见下(性质7和性质8的证明,其计算过于复杂,在此不再赘述)。
1.1.性质1的证明
\[f^*(t)=\max \limits_{x \in dom \ (f)} \{xt-f(x) \}\]以二维空间为例,$(xt-f(x))$其实是一堆直线:
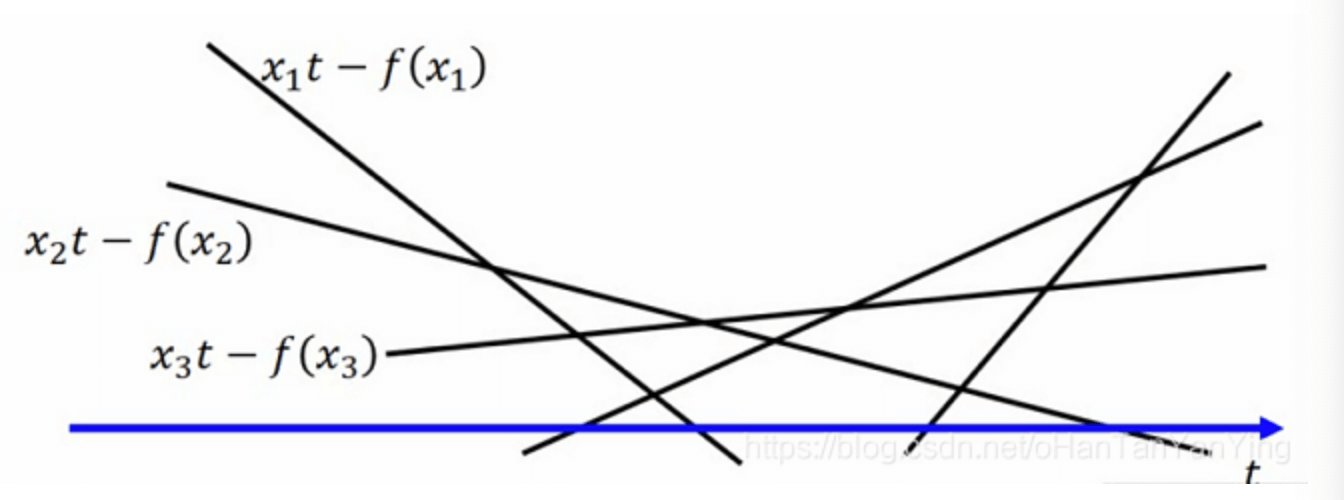
对于每一个$t$,我们需要$(xt-f(x))$最大:
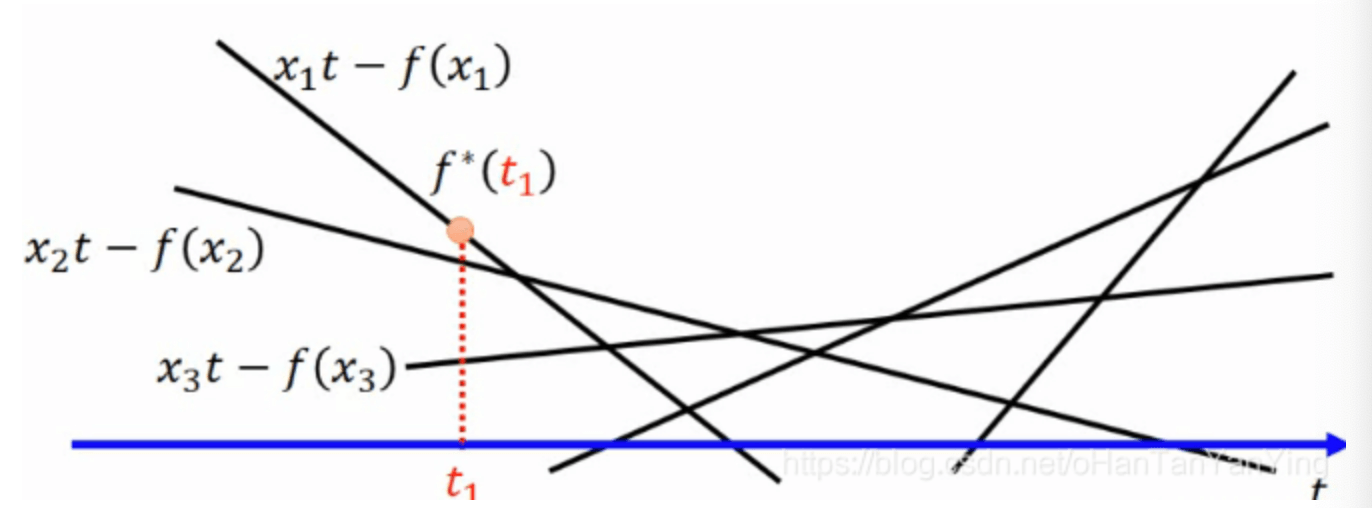
最终可得到的共轭函数$f^*(t)$的图像见下:
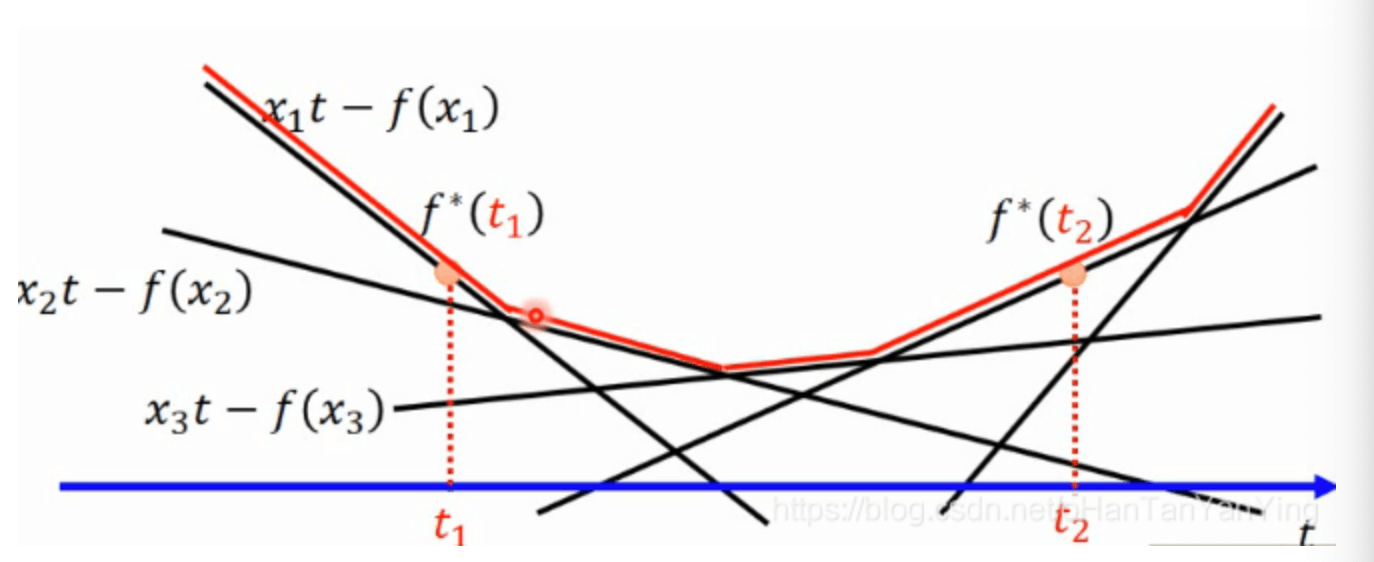
很明显,$f^*(t)$是一个凸函数。
简单来说,线性函数为凸函数,而任意多个凸函数的逐点上确界仍是凸函数,因此得证。
1.2.性质2的证明
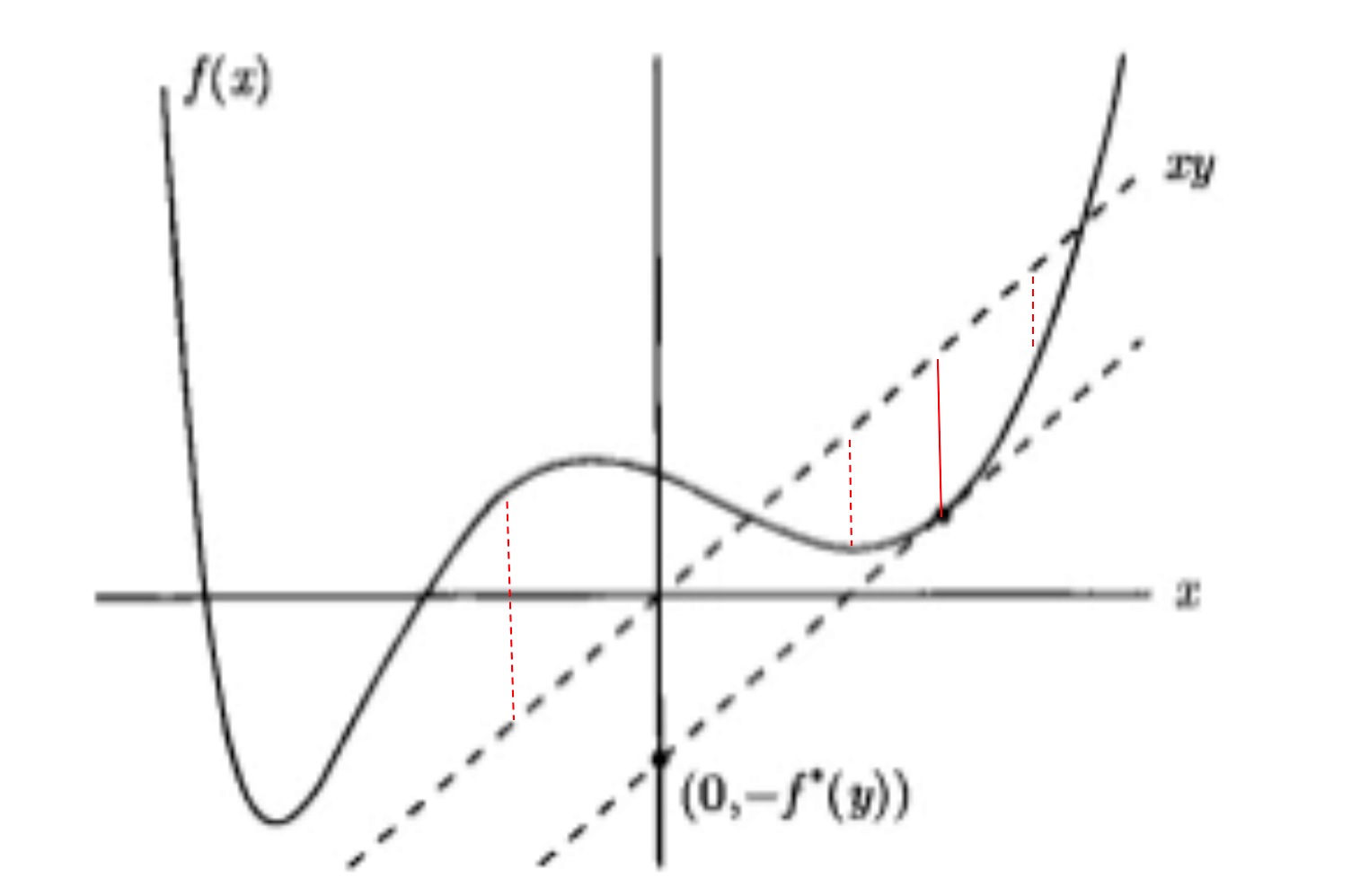
共轭函数$f^*(y)$是线性函数$yx$和$f(x)$之间的最大差值。如上图所示(以二维为例),最大差值就是红色实线,即直线$yx$与和它平行的$f(x)$的支撑超平面在$y$方向上的差值。
其他位置的红色虚线要么比红色实线短,要么代表的是负值。
而$g$作为$f$的凸闭包,二者的支撑超平面是一样的,因此性质2得证。
1.3.性质3的证明
\[f^*(y)=\sup \limits_{x \in dom \ f} (y^Tx-f(x))\] \[f^*(y) \geqslant (y^Tx-f(x))\] \[f(x) \geqslant y^T x -f^*(y)\]同理有:
\[f^*(y)=\sup \limits_{z \in dom \ f} (y^Tz-f(z))\] \[f^*(y) \geqslant (y^Tz-f(z))\] \[f(z) \geqslant y^Tz - f^*(y)\]$y^Tz$和$z^Ty$是相等的,都是一个数字(即$ 1\times 1$维)。因此:
\[f^{**}(z)=\sup \limits_{y \in dom \ f^*} (z^Ty-f^*(y))\] \[f^{**}(z) \leqslant f(z)\]性质5也在这个过程中得到了证明。
1.4.性质4的证明
函数$f(x)$的共轭函数如下:
\[f^*(t)=\max \limits_{x \in dom \ (f)} \{xt-f(x) \} \tag{1.4.1}\]由于$f(x)$是凸函数,给定$t$,关于$x$的函数$xt-f(x)$的最大值在导数等于0的时候取得:
\[(xt-f(x))'=0 \tag{1.4.2}\]即:
\[t=f'_x(x) \tag{1.4.3}\]$f’_x(x)$指的是$f(x)$对$x$求导。如果下标为$t$,则指的是对$t$求导。
也就是说给定$t$,$f’_x(x)=t$时,$xt-f(x)$取到最大值,所以$f^*(t)$又可以写成:
\[f^*(t)=xt-f(x) \ | \ f'_x(x)=t \tag{1.4.4}\]$f^*(t)$的共轭函数如下:
\[f^{**}(s) = \max \limits_{t \in dom \ (f^*)} \{ ts-f^*(t) \} \tag{1.4.5}\]同理,对于给定的$s$,$(ts-f^*(t))_t’=0$时,取最大值:
\[(ts-f^*(t))_t'=s-(f^*(t))'_t=0 \tag{1.4.6}\]结合式(1.4.4):
\[s=(f^*(t))'_t=x+ tx'_t - f'_x(x) x'_t \tag{1.4.7}\]由于式(1.4.3),$x$可以看成关于$t$的函数。
代入式(1.4.3),上述等式等价于:
\[s=(f^*(t))'_t=x+tx'_t-tx'_t=x \tag{1.4.8}\]即对于给定的$s$,$x=s$时,$ts-f^*(t)$取到最大值,即:
\[f^{**}(s)=tx-f^*(t) \tag{1.4.9}\]代入式(1.4.4):
\[f^{**}(s)=tx-f^*(t)=tx-(xt-f(x))=f(x)=f(s) \tag{1.4.10}\]1.5.性质6的证明
根据性质2的证明,我们可以知道在取到最大值时,直线$yx$和$f(x)$的支撑超平面是平行的,即:
\[\nabla f(x)=y\]又因为$f$是凸函数而且可微,所以我们是可以直接取到最大值的:
\[f^*(y)=y^Tx-f(x)=(\nabla f(x))^Tx-f(x)\]用$x^*$代替$x$:
\[f^*(y)=(\nabla f(x^*))^Tx^*-f(x^*)\]又$(\nabla f(x^{*}))^Tx^{*}=x^{* T} \nabla f(x^{*})$,所以有:
\[f^*(y)=x^{*T} \nabla f(x^*)-f(x^*)\]1.6.共轭函数的例子
求函数$f(x)=x\ln x$的共轭函数。
求解见下:
\[f^*(y)=\sup \limits_{x \in dom \ f} (y^Tx-x\ln x)\]对等式的后半部分求关于$x$的导数:
\[\frac{d}{dx} (y^Tx-x\ln x)=y^T-1-\ln x\]因为$(y^Tx-x\ln x)$是可微的,所以在取到最大值时,上述导数会等于0,因此:
\[\ln x=y^T-1\] \[x=e^{y^T-1}\]代入性质6求得最终的共轭函数$f^*(y)$:
\[f^*(y)=y^T e^{y^T-1} - e^{y^T-1} \ln (e^{y^T-1})=e^{y^T-1}\]2.拉格朗日对偶函数
拉格朗日函数及对偶问题相关内容请见:【机器学习基础】第八课:线性判别分析。
当优化问题的限制条件是⚠️线性条件⚠️时,可以利用共轭函数的一些性质方便的得到对偶问题。
- 最小化:$f_0(x)$
- 不等条件:$Ax \leqslant b$
- 等式条件:$Cx=d$
这里不等条件的比较$u<v$指的是$u$里面每一个分量都小于$v$里面对应的分量。
其对偶函数$g$为:
\[\begin{align} g(\lambda,v) & = \inf \limits_{x} (f_0(x) + \lambda^T (Ax-b) + v^T(Cx-d)) \\ & = -b^T \lambda - d^T v + \inf \limits_{x} (f_0(x) + (A^T\lambda + C^T v)^T x ) \\ &= -b^T \lambda - d^T v - f^*_0 (-A^T\lambda - C^T v ) \end{align}\]上述式子需要用到下面的推导结果:
\[\begin{align} \inf (y^Tx+f_0(x)) &= -\sup (-y^Tx-f_0(x)) \\&= -f^*(-y) \end{align}\]使$y=(A^T\lambda + C^T v)$即可。对偶函数的定义域为:
\[dom \ g=\{(\lambda,v): -A^T\lambda - C^T v \in dom \ f^*_0 \}\]3.对偶性
弱对偶性总是成立的,但是强对偶性不一定总成立。
对偶性相关讲解:对偶性。
满足强对偶性的条件:
3.1.条件1
几乎所有的凸优化问题都满足强对偶性。为什么说“几乎所有”?因为其还是有一个限制条件的,具体描述见下(称为slater条件):
对于一个凸优化问题:
- 最小化:$f_0(x)$
- 不等条件:$f_i(x) \leqslant b,i=1,\cdots,m$
- 等式条件:$h_i(x)=0,i=1,\cdots,p$
如果存在一个可行域中的点$x$使得$f_i(x)<0,i=1,\cdots,m$,那么这个凸优化问题就满足强对偶条件。