【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.EM算法简介
我们经常会从样本观察数据中,找出样本的模型参数。最常用的方法就是极大化模型分布的对数似然函数。
但是在一些情况下,我们得到的观察数据有未观察到的隐含数据(学名是“隐变量”(latent variable)),此时我们未知的有隐含数据和模型参数,因而无法直接用极大化对数似然函数得到模型分布的参数。怎么办呢?这就是EM算法可以派上用场的地方了。
EM算法也称期望最大化(Expectation-Maximum,简称EM)算法。
EM算法解决这个的思路是使用启发式的迭代方法,既然我们无法直接求出模型分布参数,那么我们可以先猜想隐含数据(EM算法的E步),接着基于观察数据和猜测的隐含数据一起来极大化对数似然,求解我们的模型参数(EM算法的M步)。由于我们之前的隐藏数据是猜测的,所以此时得到的模型参数一般还不是我们想要的结果。不过没关系,我们基于当前得到的模型参数,继续猜测隐含数据(EM算法的E步),然后继续极大化对数似然,求解我们的模型参数(EM算法的M步)。以此类推,不断的迭代下去,直到模型分布参数基本无变化,算法收敛,找到合适的模型参数。
从上面的描述可以看出,EM算法是迭代求解最大值的算法,同时算法在每一次迭代时分为两步,E步和M步。一轮轮迭代更新隐含数据和模型分布参数,直到收敛,即得到我们需要的模型参数。
对于$m$个样本观察数据$x = (x^{(1)},x^{(2)},…,x^{(m)})$中,找出样本的模型参数$\theta$,极大化模型分布的对数似然函数如下:
\[\theta = \arg \max \limits_{\theta} \sum^m_{i=1} \log P(x^{(i)};\theta)\]如果我们得到的观察数据有未观察到的隐含数据$z=(z^{(1)},z^{(2)},…,z^{(m)})$,此时我们来最大化已观测数据的对数“边际似然”(marginal likelihood):
\[\theta = \arg \max \limits_{\theta} \sum^m_{i=1} \log P(x^{(i)};\theta) = \arg \max \limits_{\theta} \sum^m_{i=1} \log \sum_{z^{(i)}} P(x^{(i)},z^{(i)} ; \theta)\]公式的具体求解过程本文不再赘述。事实上,隐变量估计问题也可通过梯度下降等优化算法求解,但由于求和的项数将随着隐变量的数目以指数级上升,会给梯度计算带来麻烦;而EM算法则可看作一种非梯度优化方法。EM算法可看作用坐标下降法(见本文第2部分)来最大化对数似然下界的过程。
然后通过一个例子来形象化的理解EM算法。假设有两枚硬币A和B,它们随机抛掷的结果见下(H为正面,T为反面):
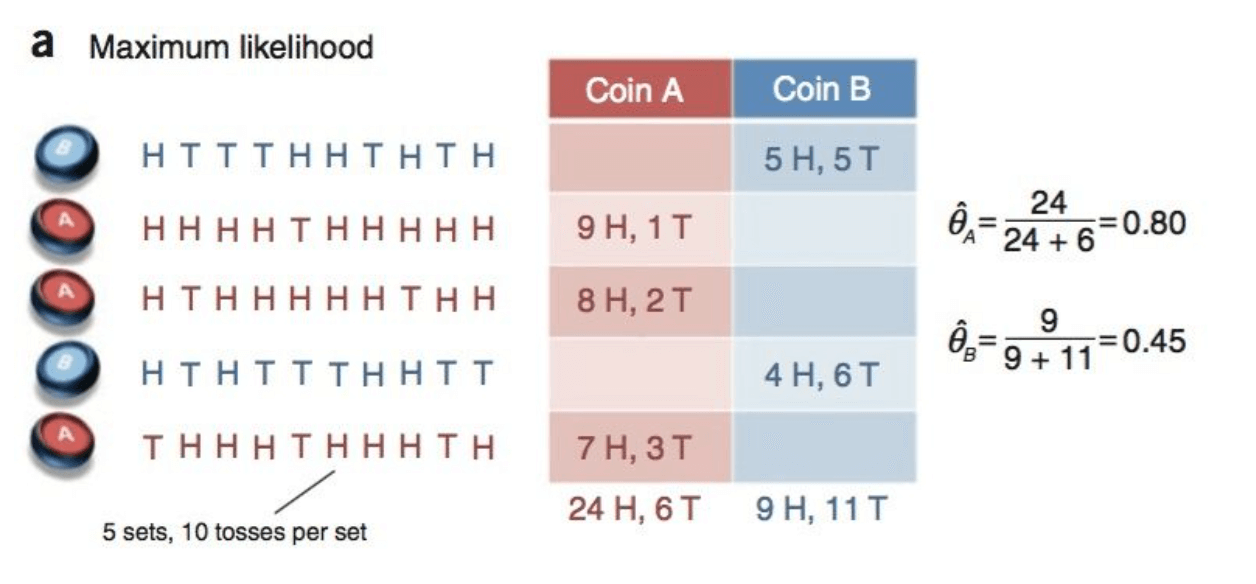
可以很容易估计出两枚硬币抛出正面的概率:
\[\theta_A = \frac{24}{24+6}=0.80\] \[\theta_B = \frac{9}{9+11}=0.45\]现在我们加入隐变量$Z=(z_1,z_2,z_3,z_4,z_5)$,代表每一轮所用的硬币,即抹去每轮投掷的硬币标记:

这种情况下,我们该如何估计$\theta_A$和$\theta_B$的值?其解决方法就是先随机初始化$\theta_A$和$\theta_B$,然后用去估计$Z$,然后基于$Z$按照最大似然概率去估计新的$\theta_A$和$\theta_B$,循环至收敛。
假设随机初始化:
\[\theta_A = 0.6\] \[\theta_B = 0.5\]对于第一轮来说,如果使用硬币A,则得到5H5T的概率为$C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5}$;如果使用硬币B,则得到5H5T的概率为$C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}$。据此,我们便可以算出第一轮使用硬币A或硬币B的概率为:
\[P_A = \frac{C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5}}{C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5} + C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}}=0.45\] \[P_B = \frac{C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}}{C^5_{10} \cdot 0.6^{0.5} \cdot 0.4^{0.5} + C^5_{10} \cdot 0.5^{0.5} \cdot 0.5^{0.5}}=0.55\]剩余轮次,以此类推可得到:

以上就是E-Step。
接下来结合硬币A的概率和投掷结果,我们利用期望可以求出硬币A和硬币B的贡献。以第二轮硬币A为例:
\[H : 0.80 * 9 =7.2\] \[T : 0.80 * 1 = 0.8\]于是我们可以得到:

重新计算$\theta_A$和$\theta_B$:
\[\theta_A = \frac{21.3}{21.3+8.6}=0.71\] \[\theta_B = \frac{11.7}{11.7 + 8.4}=0.58\]这就是M-Step。然后如此反复迭代直至参数收敛。
2.坐标下降法
坐标下降法(coordinate descent)是一种非梯度优化方法,它在每步迭代中沿一个坐标方向进行搜索,通过循环使用不同的坐标方向来达到目标函数的局部最小值。
求解极大值问题时亦称“坐标上升法”(coordinate ascent)。
不妨假设目标是求解函数$f(\mathbf x)$的极小值,其中$\mathbf x = (x_1,x_2,…,x_d)^T \in \mathbb R^d$是一个$d$维向量。从初始点$\mathbf x^0$开始,坐标下降法通过迭代地构造序列$\mathbf x^0,\mathbf x^1,\mathbf x^2,…$来求解该问题,$\mathbf x^{t+1}$的第$i$个分量$x^{t+1}_i$构造为:
\[x^{t+1}_i = \arg \min \limits_{y \in \mathbb R} f(x^{t+1}_1,...,x^{t+1}_{i-1},y,x^{t}_{i+1},...,x^t_d)\]即固定其他因变量,只留一个因变量。此时求解$f(x)$的最小值。这样问题就变得容易许多。
通过执行此操作,显然有:
\[f(\mathbf x^0) \geqslant f(\mathbf x^1) \geqslant f(\mathbf x^2) \geqslant ...\]与梯度下降法类似,通过迭代执行该过程,序列$\mathbf x^0,\mathbf x^1,\mathbf x^2,…$能收敛到所期望的局部极小点或驻点(stationary point)。
坐标下降法不需计算目标函数的梯度,在每步迭代中仅需求解一维搜索问题,对于某些复杂问题计算较为简便。但若目标函数不光滑,则坐标下降法有可能陷入非驻点(non-stationary point)。