本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.基础知识
SVM相关博客讲解:
- 【机器学习基础】第十六课:支持向量机之间隔与支持向量
- 【机器学习基础】第十七课:支持向量机之对偶问题
- 【机器学习基础】第十八课:支持向量机之核函数
- 【机器学习基础】第十九课:支持向量机之软间隔与正则化
- 【机器学习基础】第二十课:支持向量回归
- 【机器学习基础】第二十一课:支持向量机之核方法
2.Python实现
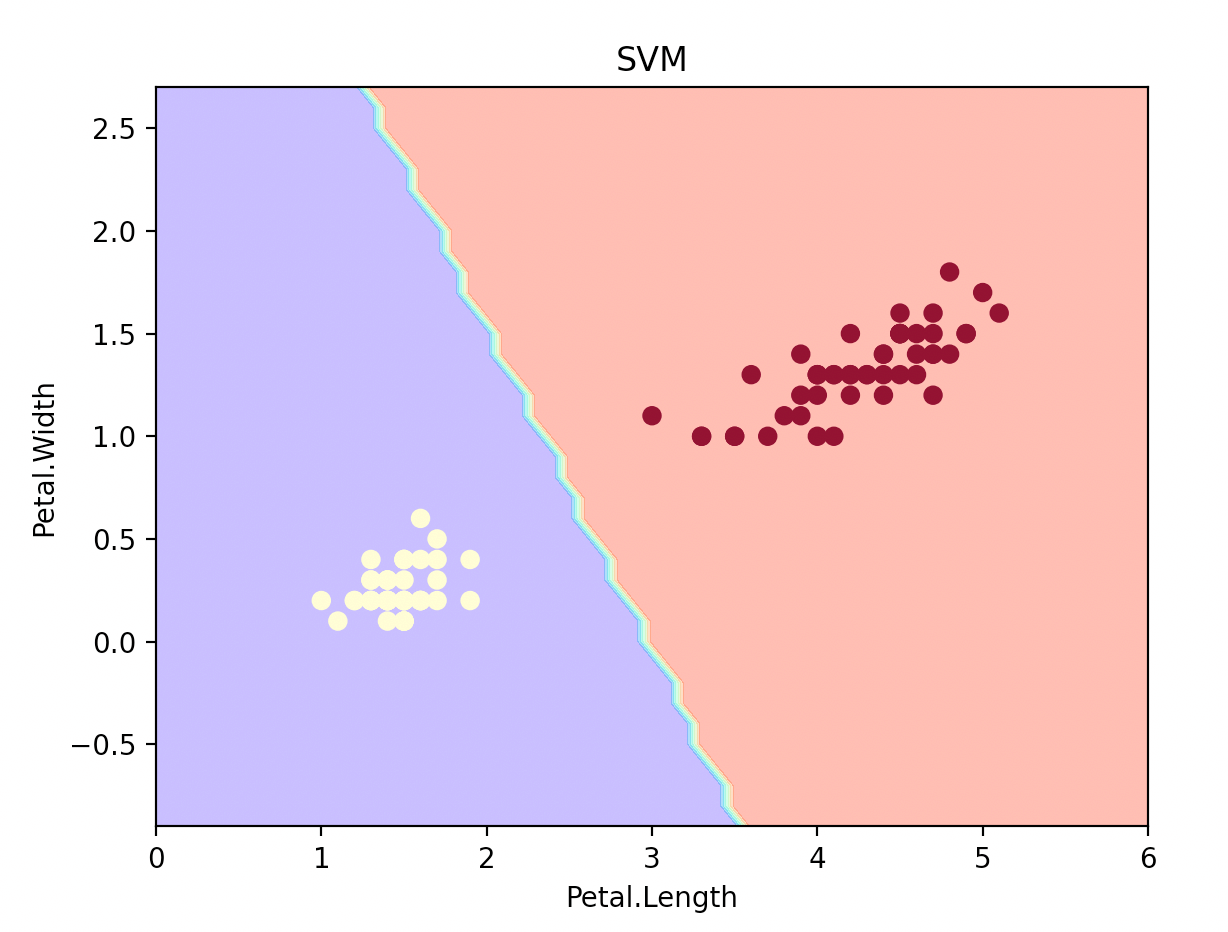
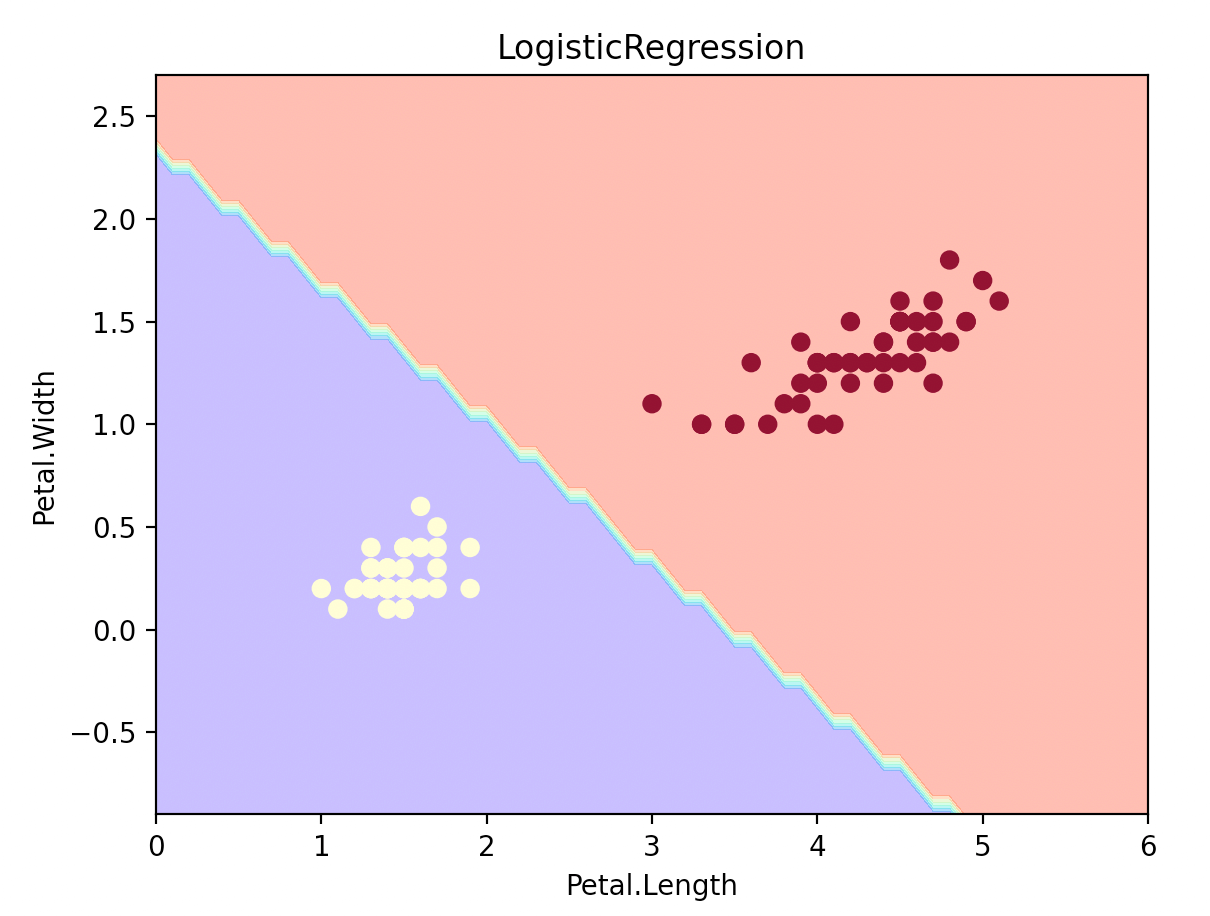
建立支持向量机并绘制决策边界,和LogisticRegression做比较:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
import numpy as np
import matplotlib.pyplot as plt
def plot_estimator(estimator, X, y, plot_title):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
plt.plot()
Z = estimator.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 参数alpha为透明度
# 参数cmap为colormap
plt.contourf(xx, yy, Z, alpha=0.4, cmap=plt.cm.rainbow)
# 参数c为颜色
# 参数alpha为透明度
# 参数cmap为colormap
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=1, cmap=plt.cm.YlOrRd)
plt.title(plot_title)
plt.xlabel('Petal.Length')
plt.ylabel('Petal.Width')
plt.show()
iris = load_iris()
X = iris.data[0:100, [2, 3]]
y = iris.target[0:100]
clf1 = SVC(kernel="linear")
clf1.fit(X, y)
clf2 = LogisticRegression()
clf2.fit(X, y)
plot_estimator(clf1, X, y, "SVM")
plot_estimator(clf2, X, y, "LogisticRegression")
👉设置正则化项:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
data = np.array(
[[-1, 2, 0], [-2, 3, 0], [-2, 5, 0], [-3, -4, 0], [-0.1, 2, 0], [0.2, 1, 1], [0, 1, 1], [1, 2, 1], [1, 1, 1],
[-0.4, 0.5, 1], [2, 5, 1]])
X = data[:, :2]
Y = data[:, 2]
# large margin
clf = SVC(C=1.0, kernel="linear")
clf.fit(X, Y)
plot_estimator(clf, X, Y, "large_margin")
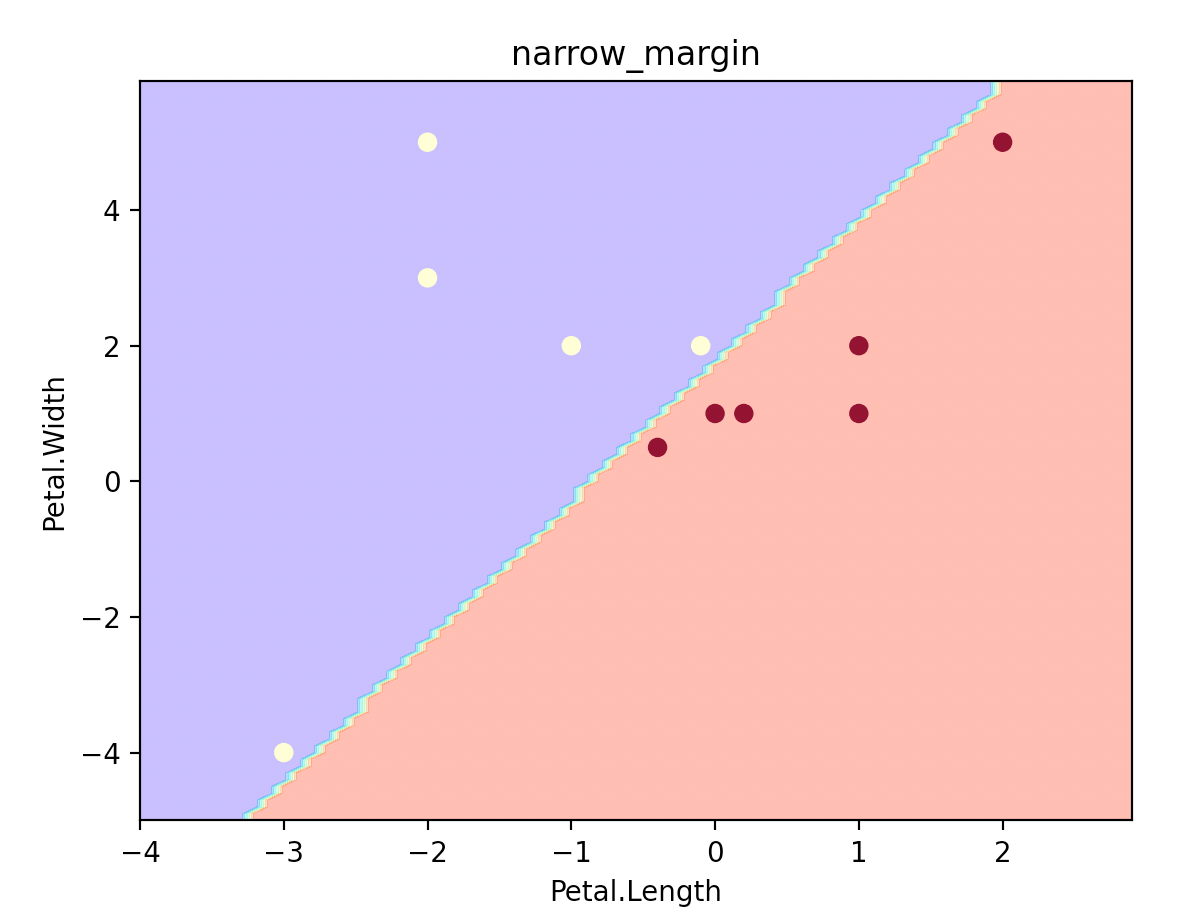
# narrow margin
clf = SVC(C=100000, kernel="linear")
clf.fit(X, Y)
plot_estimator(clf, X, Y, "narrow_margin")

👉使用不同的核函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.svm import SVC
iris = load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
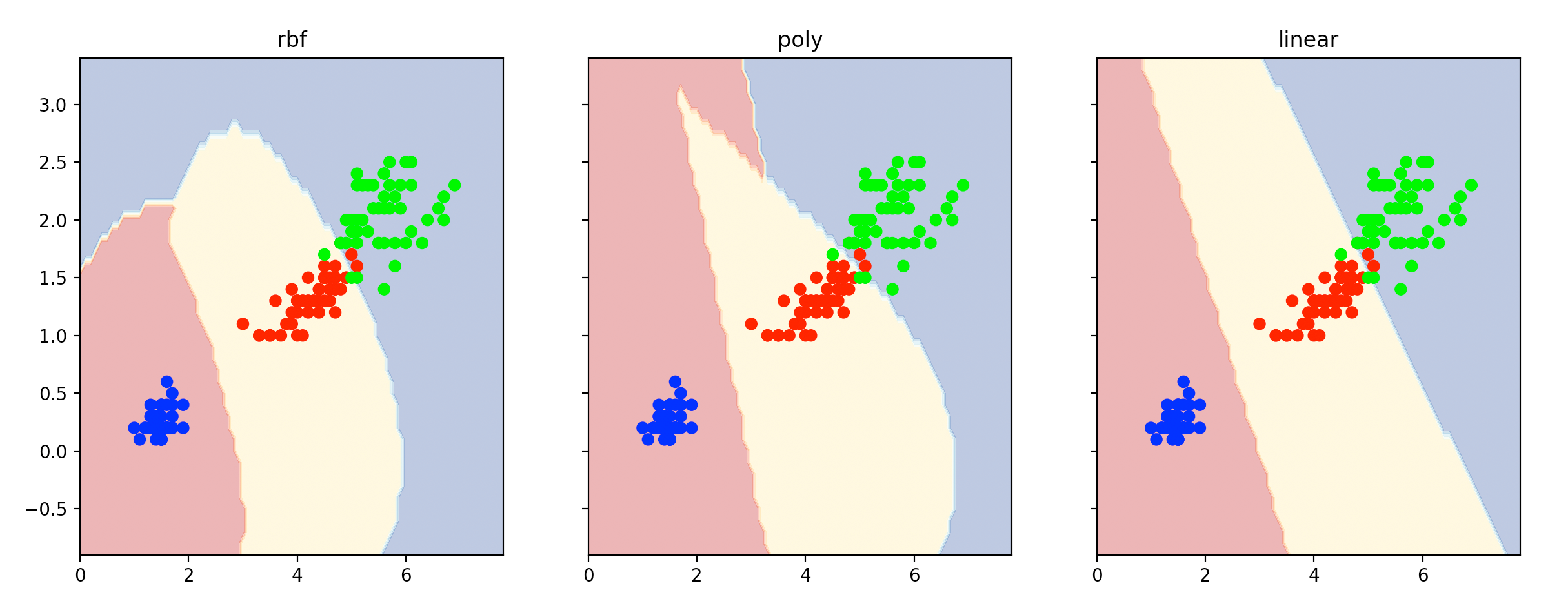
clf1 = SVC(kernel="rbf") # 非线性kernel
clf1.fit(X, y)
clf2 = SVC(kernel="poly") # 非线性kernel
clf2.fit(X, y)
clf3 = SVC(kernel="linear")
clf3.fit(X, y)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
f, axarr = plt.subplots(1, 3, sharex='col', sharey='row', figsize=(20, 5))
for idx, clf, title in zip([0, 1, 2], [clf1, clf2, clf3], ['rbf', 'poly', 'linear']):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
axarr[idx].contourf(xx, yy, Z, alpha=0.4, cmap=plt.cm.RdYlBu)
axarr[idx].scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.brg)
axarr[idx].set_title(title)
plt.show()
3.numpy数组中冒号的使用
3.1.一个冒号
1
a[i:j]
i为取值的起始位置,j为取值的终止位置(不包含j)。
1
a[i:-j]
从下标i取到倒数第j个下标之前(-1表示倒数第一个位置)。
3.2.两个冒号
1
a[i:j:h]
i为取值的起始位置,j为取值的终止位置(不包含j),h为步长。同理,可以有a[i:-j:h]。若h为负数,则表示逆序输出,这时要求起始位置下标大于终止位置。
3.3.举例说明
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
a='python'
b1=a[:]#python
b2=a[1:4:]#yth
b3=a[:-1]#pytho
b4=a[1:-2]#yth
b5=a[::-1]#nohtyp
b6=a[1:4:-1]#空值。因为按照给定的步长是无法从下标1走到4的,所以输出为空但不会报错。
b7=a[-2:-7:-2]#otp
a = np.array([[1,2,3],[4,5,6],[7,8,9],[11,12,13]])
print(a[::-1,2:0:-1])
#输出为:
#[[13 12]
# [ 9 8]
# [ 6 5]
# [ 3 2]]