本文为原创文章，未经本人允许，禁止转载。转载请注明出处。

1.ABSTRACT

本博文只介绍原文的部分章节，原文链接在本文末尾。

我们提出“exponential linear unit”（ELU），它可以加快深层神经网络的学习并提高分类精度。与ReLU、Leaky ReLU（LReLUs）和parametrized ReLU（PReLUs）一样，ELU也可以缓解梯度消失问题。但是和其他的激活函数相比，ELU具有更好的学习特性。和ReLU相比，ELU具有负值，使得其可以像BatchNorm一样将unit activations的均值推近零，并且计算复杂度较低。正因为此，ELU可以加速学习过程。尽管LReLUs和PReLUs也有负值，但是其不能确保noise-robust deactivation state（即ELU具有一定的抗噪性）。

在实验中，ELUs不仅能加快学习速度，而且在超过五层的网络上，其泛化性能明显优于ReLU和LReLUs。在CIFAR-100数据集上，在都使用BatchNorm的前提下，ELUs网络的性能明显优于ReLU网络，此外，其实BatchNorm对ELUs网络的性能并没有什么提升。ELUs网络在CIFAR-10上取得了前十的成绩，在CIFAR-100上取得了最高成绩，并且没有使用multi-view evaluation或model averaging。在ImageNet上，与具有相同结构的ReLU网络相比，ELU网络大大加快了学习速度，对于single crop+single model network，分类误差降低了10%。

2.EXPONENTIAL LINEAR UNITS (ELUS)

ELU的公式为（$0<\alpha$）：

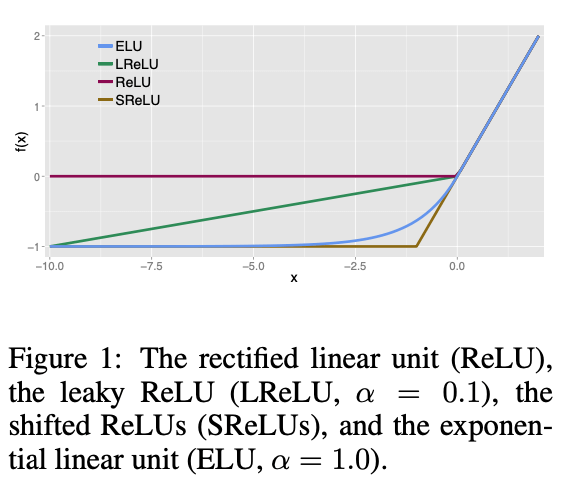
ELU的超参数$\alpha$控制着ELU接收到负值时的下限（见Fig1）。和ReLU、LReLUs一样，ELU之所以能够缓解梯度消失是因为$x$取正值时导数恒等于1。相反的，tanh激活函数和sigmoid激活函数做不到这一点。

3.EXPERIMENTS USING ELUS

在本节中，我们评估了ELUs在有监督和无监督学习中的表现。ELUs的超参数设置为$\alpha=1.0$，和其进行对比的方法有：1）ReLUs：$f(x)=\max (0,x)$；2）LReLUs：$f(x)=\max (\alpha x,x),(0<\alpha <1)$；3）Shifted ReLUs（SReLUs）：$f(x)=\max (-1,x)$。对比的时候对是否使用BatchNorm也进行了区分。使用了如下数据集的benchmark：1）MNIST数据集（灰度图像，共10个类别，训练集60k张图像，测试集10k张图像）；2）CIFAR-10（彩色图像，共10个类别，训练集50k张图像，测试集10k张图像）；3）CIFAR-100（彩色图像，100个类别，训练集50k张图像，测试集10k张图像）；4）ImageNet（彩色图像，1000个类别，训练集1.3M张图像，测试集100k张图像）。

3.1.MNIST

3.1.1.LEARNING BEHAVIOR

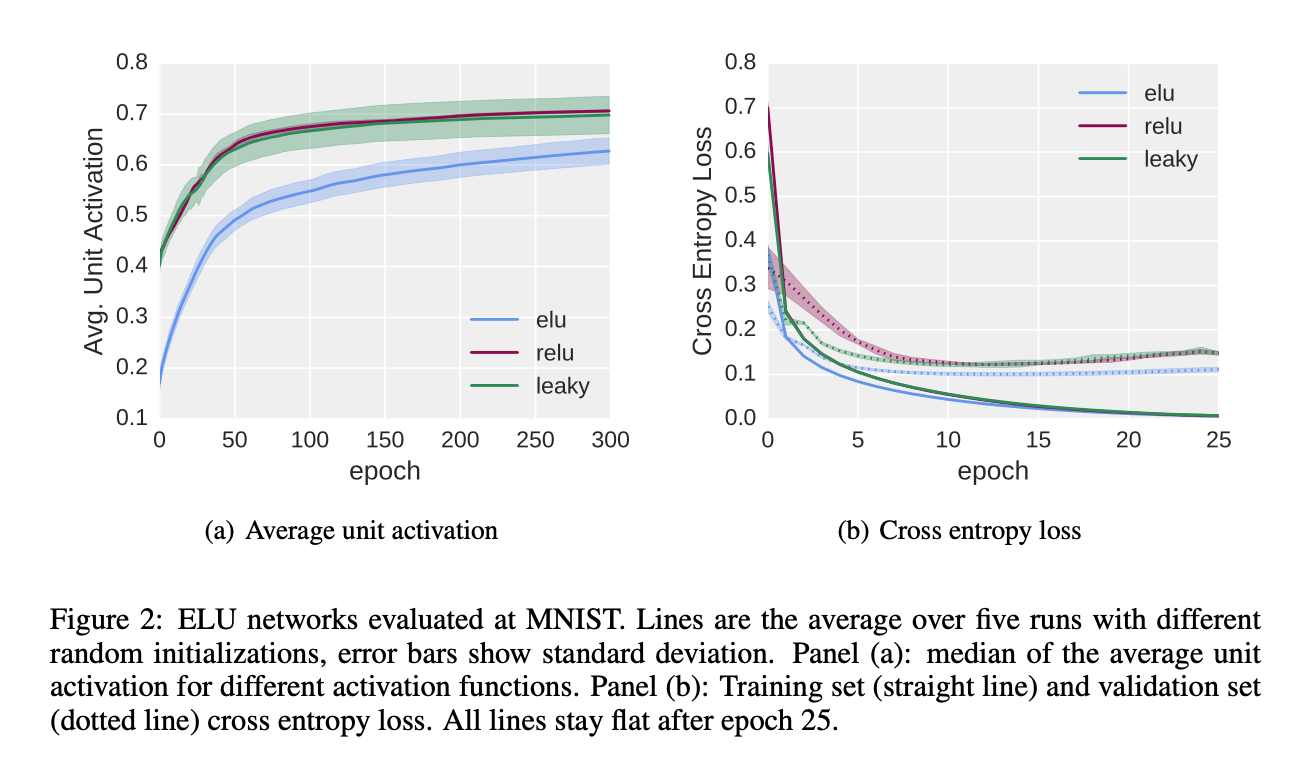
我们首先要验证，和其他激活函数相比，ELUs的平均激活值更接近于0。在MNIST数据集上训练一个全连接深度神经网络，激活函数分别使用：ELUs（$\alpha=1.0$），ReLUs，LReLUs（$\alpha=0.1$）。网络共有八个隐藏层，每个隐藏层有128个神经元，训练了300个epoch，学习率为0.01，mini-batch size=64。权重初始化遵循论文“He, K., Zhang, X., Ren, S., and Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In IEEE International Conference on Computer Vision (ICCV), 2015.”。在每次epoch之后，我们分别计算每个神经元的平均激活值。结果见Fig2。

3.1.2.AUTOENCODER LEARNING

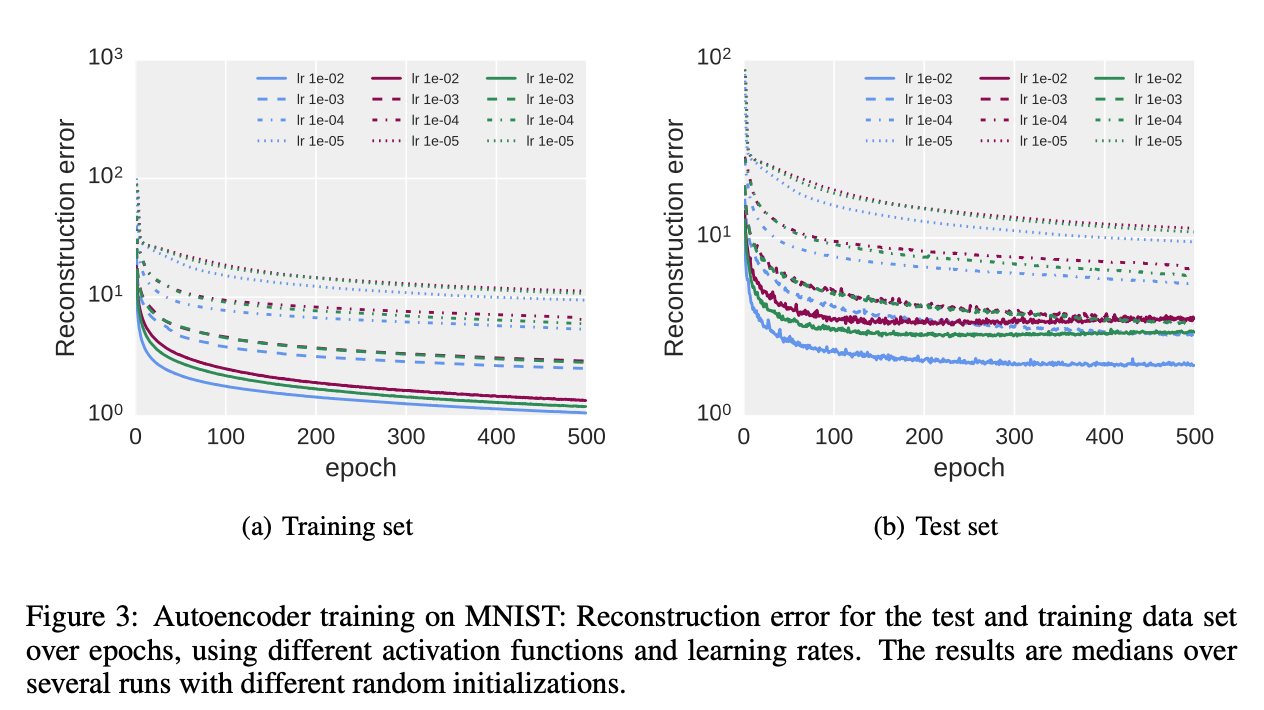
本小节评估ELU网络在无监督学习下的表现，我们遵循论文“Martens, J. Deep learning via Hessian-free optimization. In Fu ̈rnkranz, J. and Joachims, T. (eds.), Proceedings of the 27th International Conference on Machine Learning (ICML10), pp. 735–742, 2010.”和论文“Desjardins, G., Simonyan, K., Pascanu, R., and Kavukcuoglu, K. Natural neural networks. CoRR, abs/1507.00210, 2015. URL http://arxiv.org/abs/1507.00210.”，在MNIST数据集上训练了一个深度autoencoder。encoder部分包含四个全连接隐藏层，神经元数分别为1000、500、250、30。decoder和encoder呈对称结构。我们使用梯度下降法，mini-batch size=64，epoch=500，学习率分别为$(10^{-2},10^{-3},10^{-4},10^{-5})$。结果见Fig3。

3.2.COMPARISON OF ACTIVATION FUNCTIONS

本节我们将证明ELUs具有更好的学习特性。此外，我们还会展示ELUs比ReLUs+BatchNorm的表现更好。我们使用CIFAR-100数据集和一个相对简单的CNN网络以便比较。

我们使用的CNN网络有11个卷积层（layers $\times$ units $\times$ receptive fields）：

• $[1\times 192 \times 5]$
• $[1 \times 192 \times 1,1\times 240 \times 3]$
• $[1\times 240 \times 1,1\times 260 \times 2]$
• $[1\times 260 \times 1,1\times 280 \times 2]$
• $[1\times 280 \times 1,1\times 300 \times 2]$
• $[1\times 300 \times 1]$
• $[1\times 100 \times 1]$

每个stack之后接一个$2\times 2$的max pooling，步长为2。每一个stack我们都使用了dropout，其中drop-out rate分别为$(0.0,0.1,0.2,0.3,0.4,0.5,0.0)$。L2 weight decay设为0.0005。学习率的变化为（iterations[learning rate]）：0-35k[0.01]，35k-85k[0.005]，85k-135k[0.0005]，135k-165k[0.00005]。为了公平比较，我们对每个网络都使用了这种学习率变化策略。momentum=0.9。按照论文“Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. Maxout networks. ArXiv e-prints, 2013.”的方式对数据集进行预处理。此外，图像的每个边缘都被padding了4个0像素。模型在$32\times 32$大小的裁剪图像上（并加以随机的水平翻转）进行训练。除此之外，我们没在训练阶段再使用其他的数据扩展。每个网络都以不同的权重初始化方式跑了10次。我们会在同一权重初始化下，比较不同的激活函数。

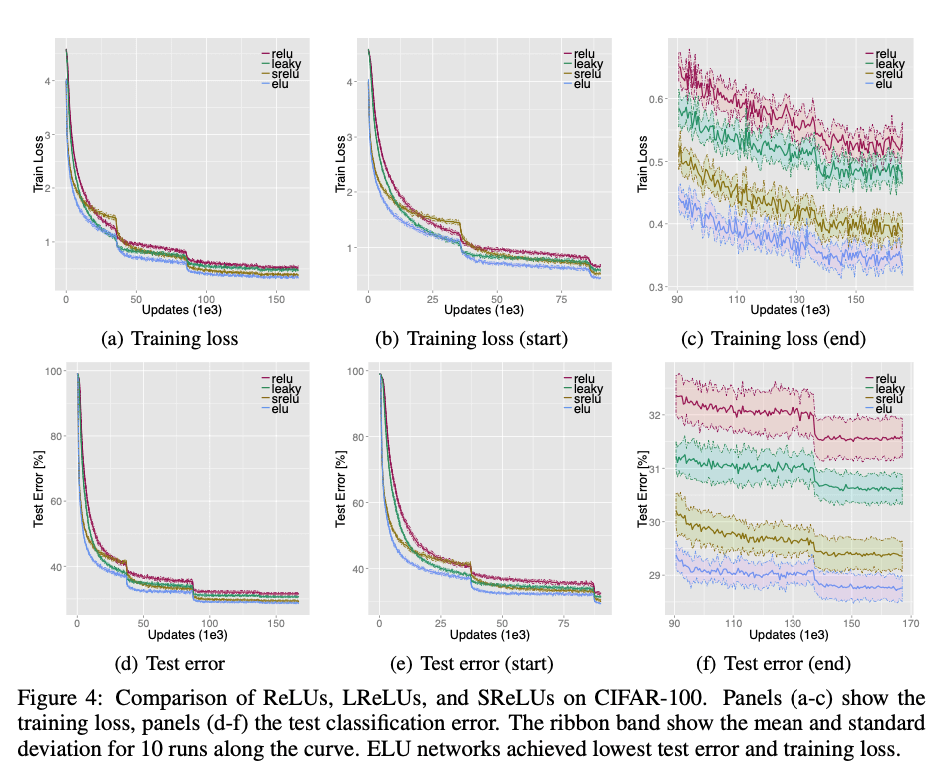
使用不同激活函数的网络的mean test error见Fig4。ELUs的平均test error为$28.75 (\pm 0.24)\%$，SReLUs的平均test error为$29.35(\pm 0.29)\%$，ReLUs的平均test error为$31.56(\pm 0.37)\%$，LReLUs的平均test error为$30.59(\pm 0.29)\%$。无论是training loss还是test error，ELUs都是最低的。并且经过统计学假设检验（Wilcoxon signed-rank test，p-value<0.001），ELUs确实是优于其他激活函数。BatchNorm提升了ReLU网络和LReLU网络的表现，但是却没有提升ELU网络和SReLU网络的表现（见Fig5）。从Fig5可以看出，ELUs比ReLUs+BatchNorm的表现更好（Wilcoxon signed-rank test，p-value<0.001）。

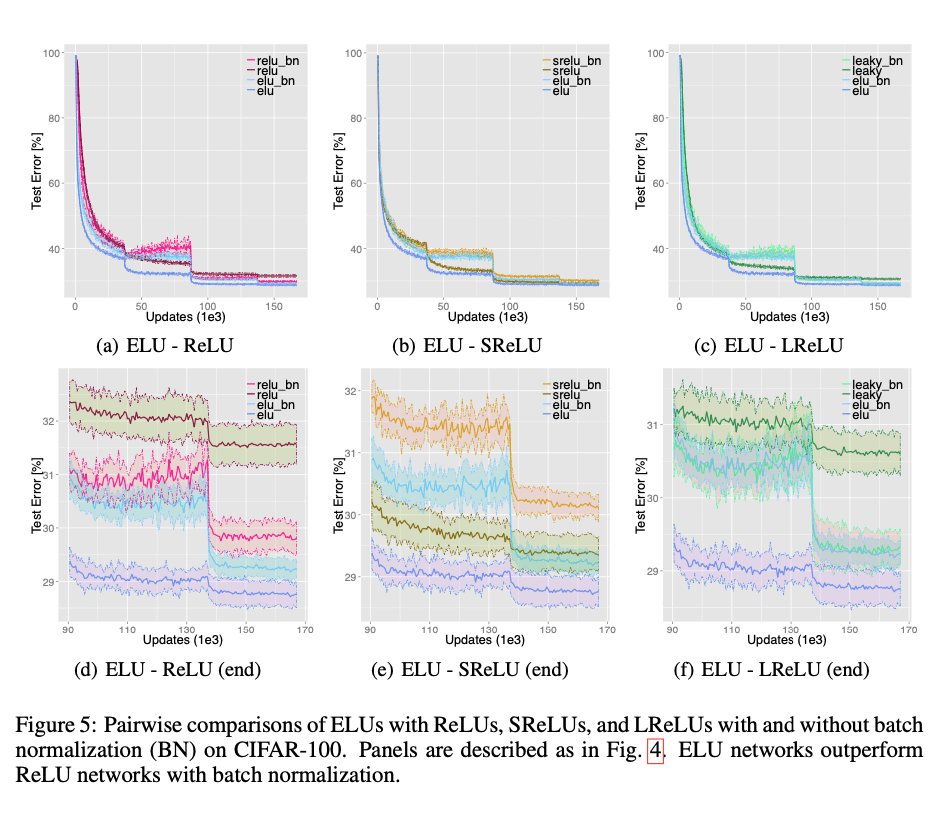
3.3.CLASSIFICATION PERFORMANCE ON CIFAR-100 AND CIFAR-10

接下来的实验着重强调了ELU网络的泛化性能。这里我们使用一个有18个卷积层的CNN：

• $[1\times 384 \times 3]$
• $[1\times 384 \times 1,1\times 384\times 2,2\times 640 \times 2]$
• $[1\times 640\times 1,3\times 768 \times 2]$
• $[1\times 768 \times 1,2\times 896 \times 2]$
• $[1\times 896 \times 3 , 2\times 1024 \times 2]$
• $[1\times 1024 \times 1,1\times 1152 \times 2]$
• $[1\times 1152 \times 1]$
• $[1\times 100 \times 1]$

drop-out rate，max pooling，L2 weight decay，momentum，数据预处理，padding，cropping等设置都和之前章节保持一致。初始学习率设置为0.01，每35k次迭代缩小10倍。mini-batch size=100。

比较结果见表1。在CIFAR-10数据集上，ELU网络的成绩是第二好。在CIFAR-100数据集上是第一好。这也是目前CIFAR-100数据集上的最好结果。

3.4.IMAGENET CHALLENGE DATASET

最后，我们在1000个类别的ImageNet数据集上评估了ELU网络。它包括1.3M的训练集，50k的验证集和100k的测试集。我们使用一个15层的CNN：

• $1\times 96 \times 6$
• $3\times 512 \times 3$
• $5\times 768 \times 3$
• $3\times 1024 \times 3$
• $2\times 4096 \times FC$
• $1\times 1000 \times FC$

每个stack之后都接一个$2\times 2$的max pooling，步长为2。在第一个FC层之前使用一个3 level的spatial pyramid pooling（SPP）。L2 weight decay=0.0005，对最后两个FC层使用dropout（rate=50%）。图像被resize到$256\times 256$，且每个像素都进行去均值化。训练阶段使用的是$224 \times 224$大小的crop并施加随机的水平翻转。除此之外，在训练阶段，我们没有使用其他的数据扩展。

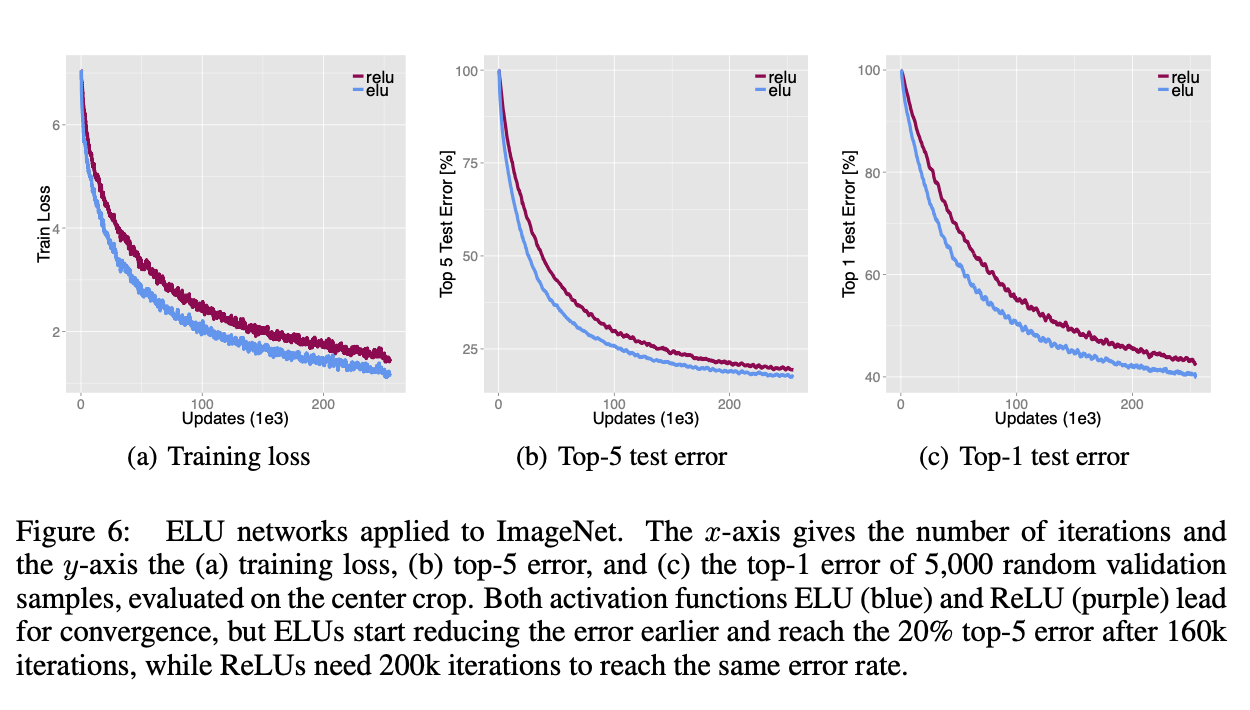
结果见Fig6。Fig6（b）显示ELUs更早的开始降低error。ELU网络达到20%的error rate仅需160k次迭代，但是ReLU网络需要200k次迭代才能达到一样的error rate。single-model的表现是基于single center crop评估的，没有额外的扩展，最终top-5 validation error低于10%。

目前在ImageNet上，ELU网络会比ReLU网络慢5%左右。例如10k次迭代，ELU网络需要12.15小时，而ReLU网络需要11.48小时（个人理解：ELU网络虽然在训练相同迭代次数的前提下，速度慢于ReLU网络，但是ELU网络学习能力更强，收敛所用的迭代次数更少，错误率也更低）。我们未来将使用更快的指数函数来改进ELU。

4.原文链接

👽FAST AND ACCURATE DEEP NETWORK LEARNING BY EXPONENTIAL LINEAR UNITS (ELUS)

• Previous
  【Tensorflow基础】第十三课：Word2Vec
• Next
  【论文阅读】GAUSSIAN ERROR LINEAR UNITS (GELUS)