本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.层次聚类的优点和缺点
层次聚类:
层次聚类优点:
- 可以产生可视化聚类结果。
- 可以等结构产生后,再进行聚类。
- 不用一开始决定要分多少类。
层次聚类缺点:
- 计算速度缓慢。
2.k-means聚类
3.k-means++聚类
k-means聚类的局限性在于聚类结果的好坏依赖于初始聚类中心的选择,且算法常会陷入局部最优。为了解决这个局限性,引入k-means++算法。k-means++算法不再随机选择初始聚类中心,而是保证初始聚类中心之间的距离尽可能远,这样就能保证最后的分类结果达到类内距离小、类间距离大的效果。
k-means++算法和k-means聚类只有在选择初始聚类中心时不同,其他步骤均相同。k-means++算法选择初始聚类中心的步骤:
- 随机选择一个样本点作为第一个聚类中心。
- 计算剩下每个样本与当前已有聚类中心之间的最短距离(即与最近的一个聚类中心的距离),用$D(x)$表示。
- 计算每个样本被选为下一个聚类中心的概率:$\frac{D(x)^2}{\sum_{x \in \mathcal{X}} D(x)^2}$。最后,按照轮盘法选择出下一个聚类中心。
- 重复第2,3步直到选择出k个初始聚类中心。
举个例子说明下k-means++初始聚类中心的选择过程,例如有8个样本见下(假设k=2):
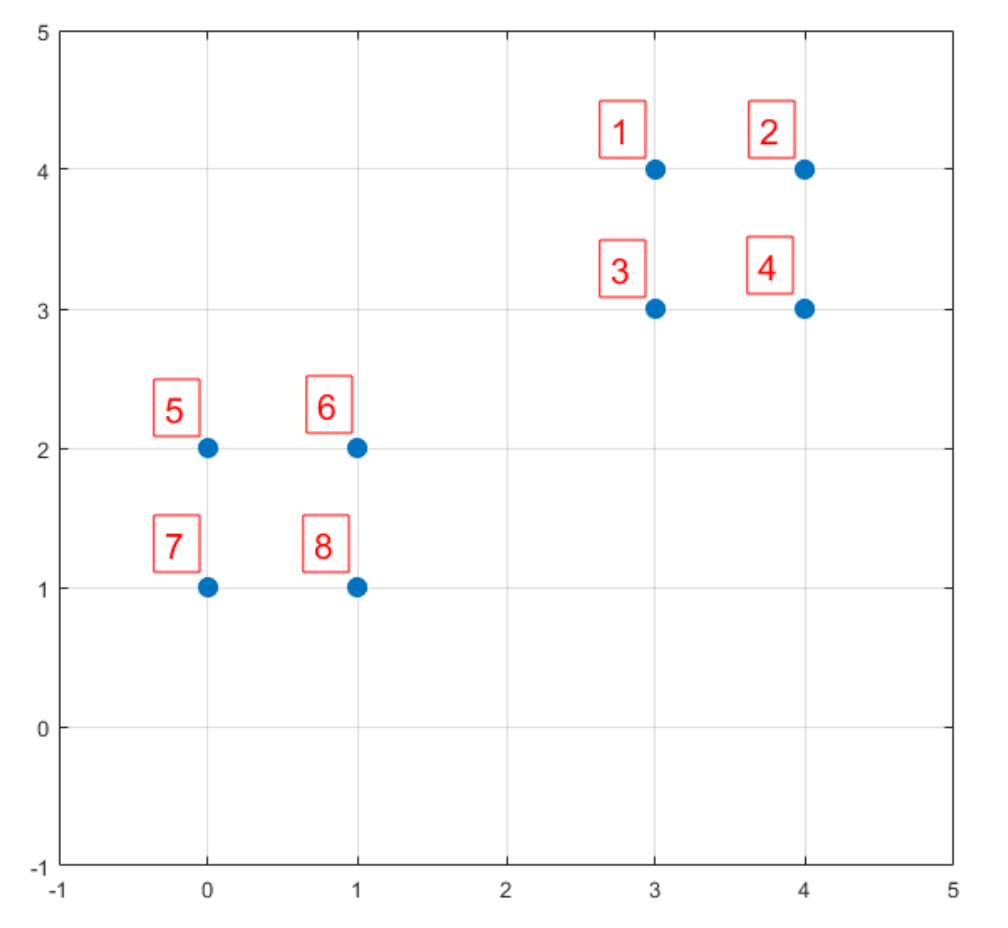
假设随机选择样本6作为第一个初始聚类中心,依次计算剩余样本到第一个初始聚类中心的距离以及其被选中作为第二个初始聚类中心的概率:
| 样本 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| $D(x)^2$ | 8 | 13 | 5 | 10 | 1 | 0 | 2 | 1 |
| $P(x)$ | 0.2 | 0.325 | 0.125 | 0.25 | 0.025 | 0 | 0.05 | 0.025 |
| $\sum P$ | 0.2 | 0.525 | 0.65 | 0.9 | 0.925 | 0.925 | 0.975 | 1 |
上表中的最后一行是累加概率。k-means++并不是直接把概率最高的样本2作为第二个初始聚类中心,而是通过轮盘法选出第二个初始聚类中心。
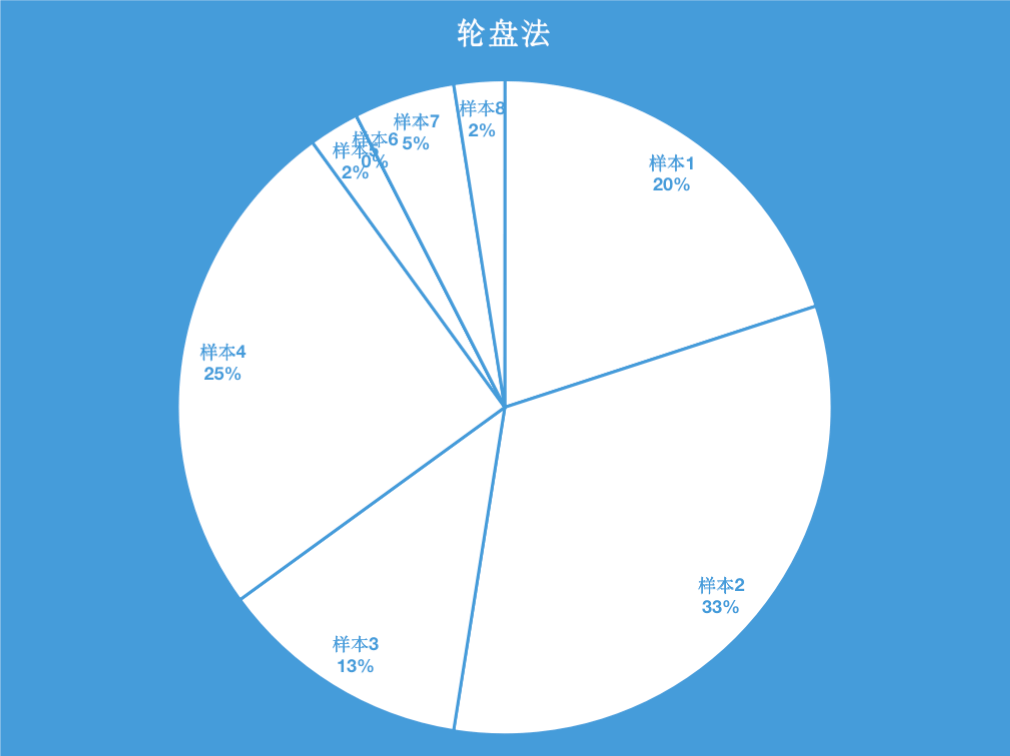
就像掷飞镖一样,靶子如上所示,通过掷飞镖的方式选择出第二个初始聚类中心,显然掷到样本1、样本2、样本3和样本4的概率是大的(其中,掷到样本2的概率是最大的),掷到这四个样本的概率高达90%,并且这4个样本正好是离第一个初始聚类中心比较远的4个点。在实际实现时,可在[0,1]范围内随机产生一个随机数,如果随机数落在[0,0.2)的区间内,则选择样本1作为第二个初始聚类中心,如果随机数落在[0.2,0.525)的区间内,则选择样本2作为第二个初始聚类中心,剩下的以此类推。
4.elkan k-means算法
在传统的k-means聚类算法中,我们在每轮迭代时,都要计算所有的样本点分别到所有聚类中心的距离,这会很耗时。因此elkan k-means算法从这块入手加以改进,减少不必要的距离计算。
elkan k-means算法利用两边之和大于等于第三边以及两边之差小于等于第三边的三角形性质,来减少距离的计算。例如对于一个样本点$x$和两个聚类中心$\mu_1,\mu_2$,如果我们预先计算出了两个聚类中心之间的距离$D(\mu_1,\mu_2)$,如果此时有$2D(x,\mu_1) \leqslant D(\mu_1,\mu_2)$,我们便可判断出$D(x,\mu_1) \leqslant D(x,\mu_2)$,此时我们不需要再计算$D(x,\mu_2)$。推导见下:
\[2D(x,\mu_1) = D(x,\mu_1) + D(x,\mu_1) \leqslant D(\mu_1,\mu_2) \leqslant D(x,\mu_1) + D(x,\mu_2)\]但是如果数据是稀疏的,有太多的缺失值,就无法使用该算法了。
5.API介绍
使用sklearn.cluster中的KMeans函数:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def __init__(
self,
n_clusters=8,
init='k-means++',
n_init=10,
max_iter=300,
tol=1e-4,
precompute_distances='auto',
verbose=0,
random_state=None,
copy_x=True,
n_jobs=1,
algorithm='auto'
)
参数详解:
n_clusters:聚类的k值,即聚成几类。默认k=8。init:初始聚类中心的产生方式。该函数提供了3种方式:random:随机选择初始聚类中心,即k-means算法选择初始聚类中心的方式。k-means++:k-means++算法选择初始聚类中心的方式。- (n_clusters,n_features)大小的ndarray,可以直接指定初始聚类中心。
n_init:算法运行的次数。因为初始聚类中心的随机性,所以每次运行的结果也会不同。默认是10次,取最好的结果。max_iter:单次运行时的最大迭代次数。默认最多为300次迭代。tol:默认为$1e-4$。如果连续两次迭代的聚类中心的差异小于tol,则退出迭代。precompute_distances:是否提前计算好距离。如果为“True”,则会提前计算好距离,算法运行会更快但也会更占内存。如果为“False”,则不提前计算好距离。如果为“auto”,若样本数和n_clusters的乘积大于1200万则不提前计算距离,否则则提前计算距离。verbose:是否输出详细信息。默认为0,不输出。random_state:可以是int型、RandomState instance或者None,默认是None。当是int型时,其为随机数生成器的种子。当是RandomState instance时,其为随机数生成器。当是None时,其为使用np.random的RandomState instance,也是一个随机数生成器。copy_x:在提前计算距离时,如果将数据中心化,则会得到更准确的结果。如果copy_x为True,则不修改原始数据,即不进行中心化。如果copy_x为False,则会修改原始数据(即中心化处理),并在返回时还原。但是由于会对数据进行加减平均的操作,所以还原后的数据可能和原始数据有微小的差别。默认为True。n_jobs:int类型,为并行运行的进程数,即可以同时运行n_init设置好的多次运算。如果为-1,则所有CPU都会被使用。如果为1,则只有一个进程,用于debugging。如果n_jobs小于-1,则用到的CPU数为n_cpus+1+n_jobs。algorithm:优化算法。当algorithm为“full”时,使用经典的EM风格的算法,即普通的k-means算法。当algorithm为“elkan”时,使用elkan k-means算法。当algorithm为“auto”时,如果是密集数据则使用“elkan”,如果是稀疏数据(通常指含有大量缺失值)则使用“full”。
6.实际案例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from sklearn.datasets import load_iris
iris = load_iris()
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, init='k-means++', random_state=123)
y_kmeans = kmeans.fit_predict(iris.data)
import matplotlib.pyplot as plt
plt.scatter(iris.data[y_kmeans == 0, 2], iris.data[y_kmeans == 0, 3], s=100, c="red", label="Cluster1")
plt.scatter(iris.data[y_kmeans == 1, 2], iris.data[y_kmeans == 1, 3], s=100, c="blue", label="Cluster2")
plt.scatter(iris.data[y_kmeans == 2, 2], iris.data[y_kmeans == 2, 3], s=100, c="green", label="Cluster3")
# 画中心点
plt.scatter(kmeans.cluster_centers_[:, 2], kmeans.cluster_centers_[:, 3], s=100, c="yellow", label="Centroids")
plt.title("Clusters of Iris")
plt.xlabel("Petal.Length")
plt.ylabel("Petal.Width")
plt.legend()
plt.show()
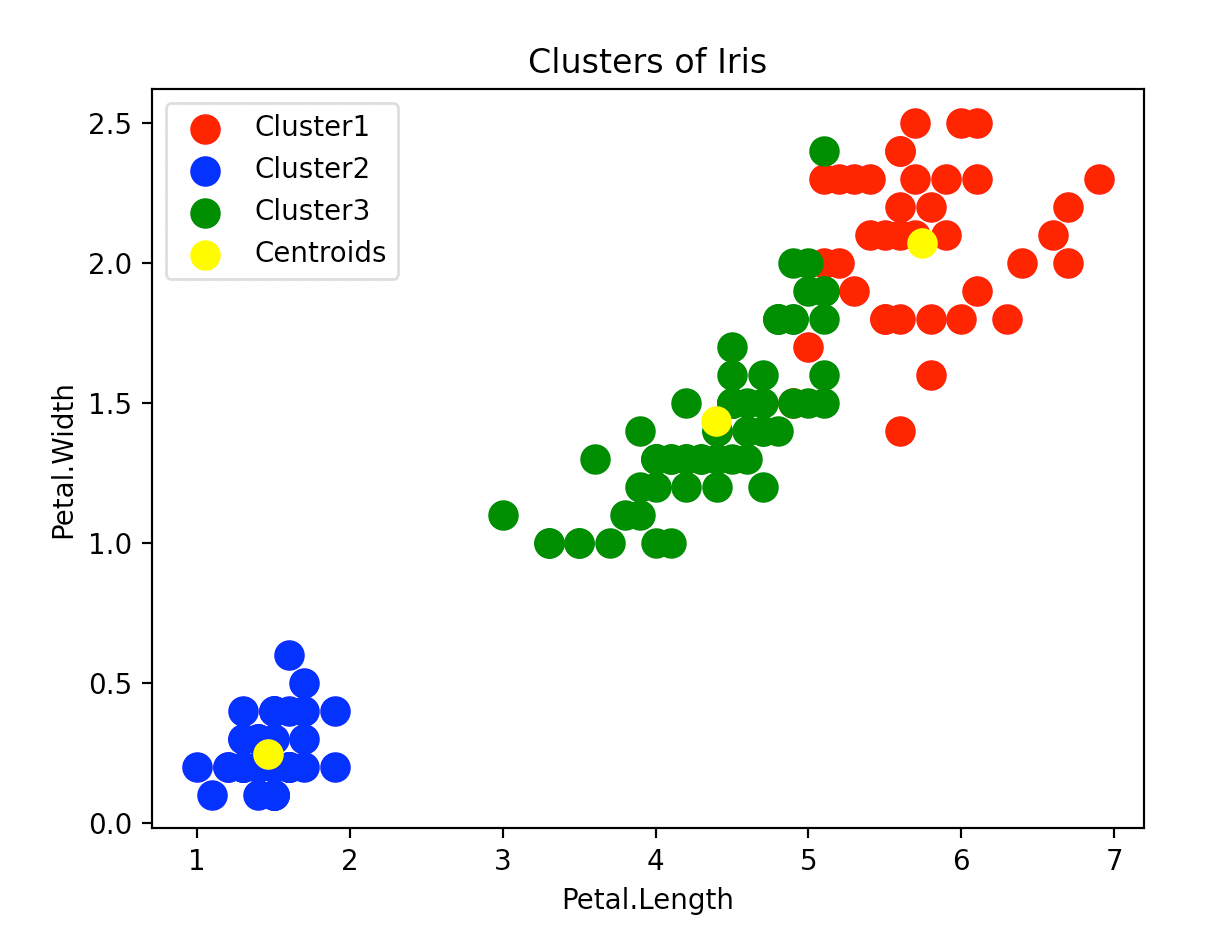
因为画图只用了两个维度,所以有的样本看起来离所属的聚类中心并不是最近的。
.cluster_centers_可用于输出聚类中心的坐标。