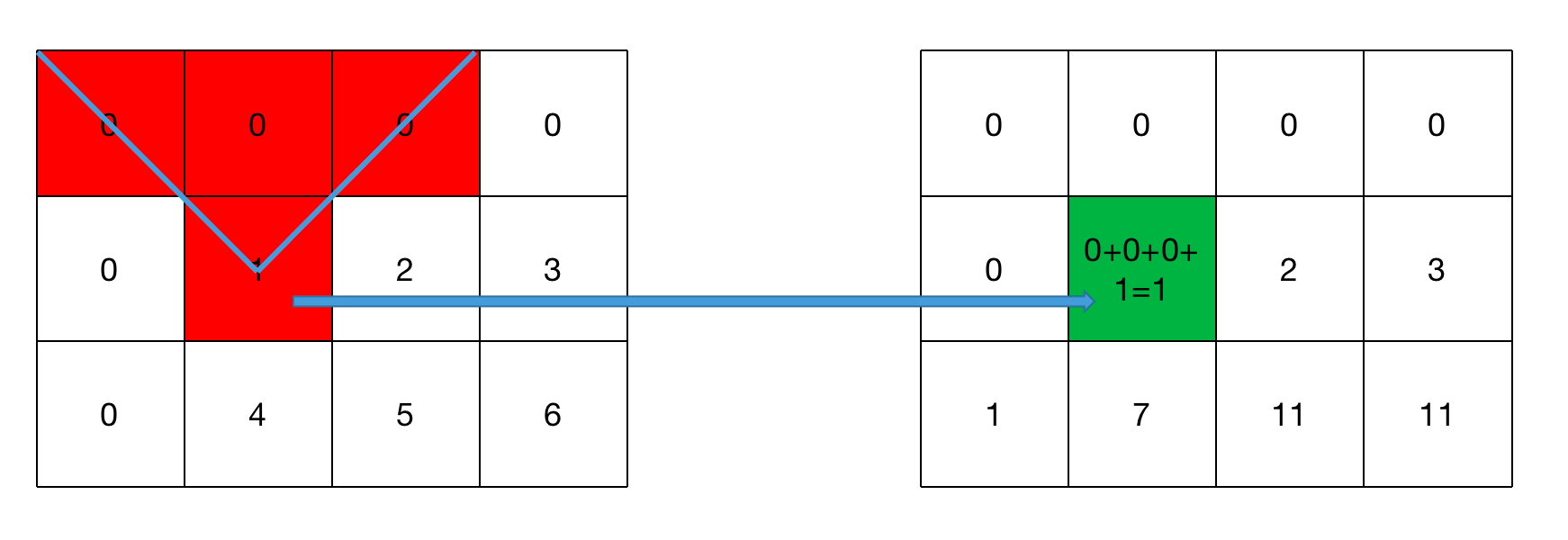本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.积分图原理
积分图(Integral Image)的定义:取图像左上侧的全部像素计算累加和,并用这个累加和替换图像中的每一个像素,使用这种方式得到的图像称为积分图像。
\[I(x,y)=\sum_{\begin{matrix} x' \leqslant x \\ y' \leqslant y \\ \end{matrix}} i(x',y')\]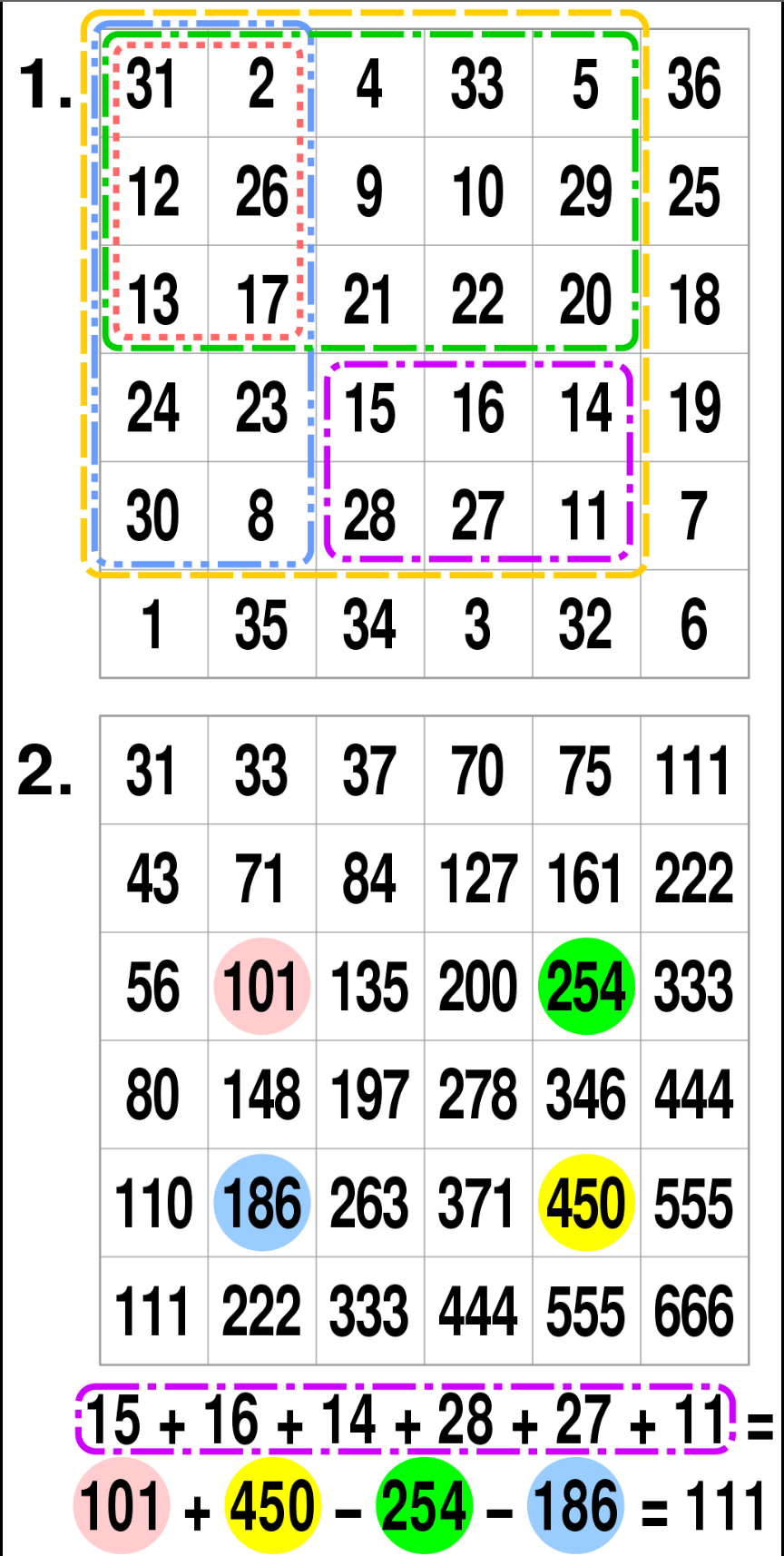
积分图又称总和面积表(summed area table,简称SAT),是一个快速且有效的对一个网格的矩形子区域中计算和的数据结构和算法。
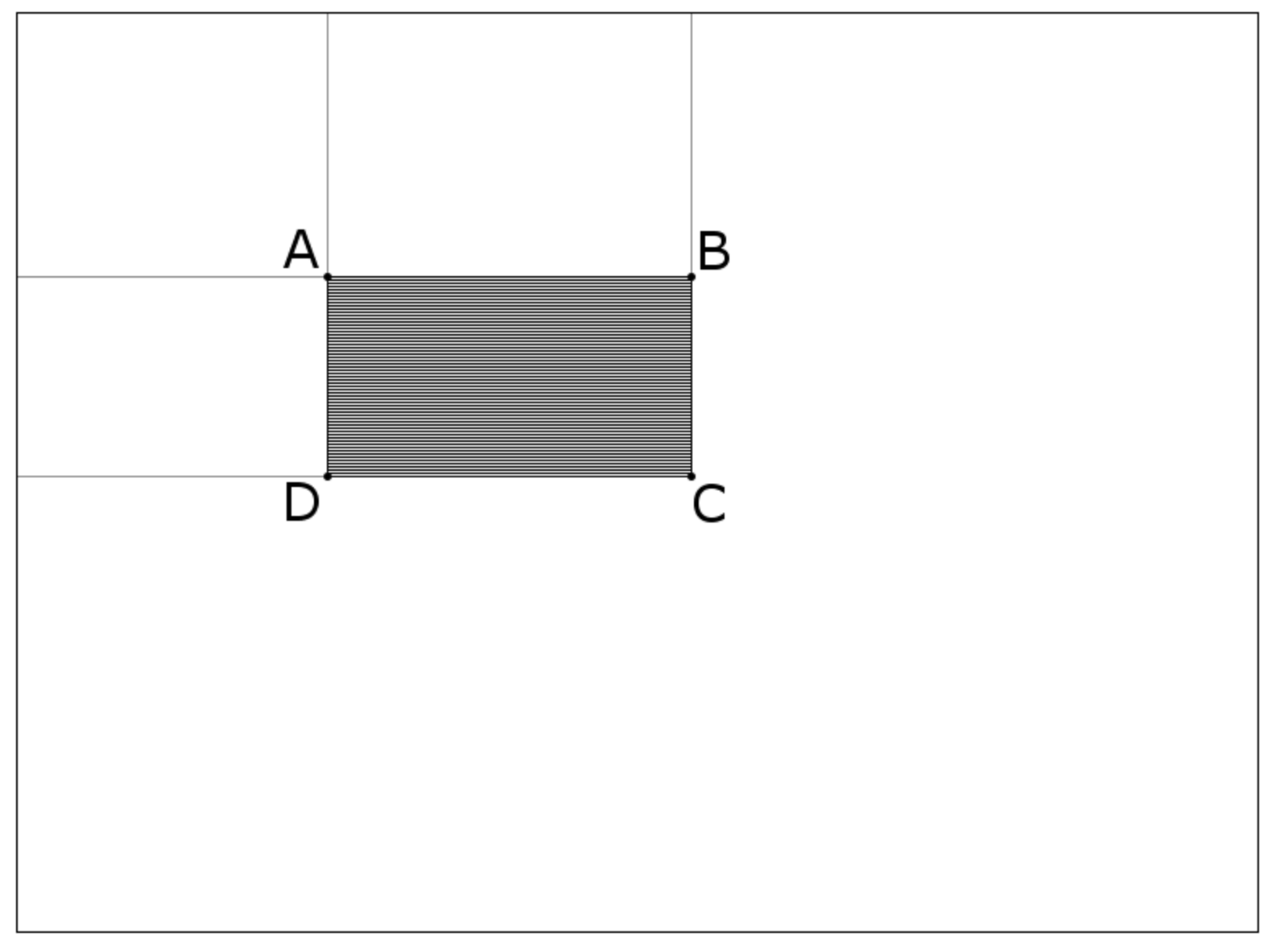
积分图可以只遍历一次图像即可有效的计算出来,其通常被用来加速计算过程。一旦积分图计算完毕,对任意矩形区域的和的计算就可以在常数时间内(一次加法,两次减法)完成。如下图中,阴影矩形区域的值:
2.cv::integral
cv::integral有三种重载形式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//第一种重载形式
void integral(
InputArray src,
OutputArray sum,
int sdepth = -1
);
//第二种重载形式
void integral(
InputArray src,
OutputArray sum,
OutputArray sqsum,
int sdepth = -1,
int sqdepth = -1
);
//第三种重载形式
void integral(
InputArray src,
OutputArray sum,
OutputArray sqsum,
OutputArray tilted,
int sdepth = -1,
int sqdepth = -1
);
参数详解:
InputArray src:大小为$W \times H$的输入图像。类型为8-bit或浮点型(32f或64f)。OutputArray sum:输出大小为$(W+1) \times (H+1)$的积分图,类型为32-bit整型或浮点型(32f或64f)。- \[\texttt{sum} (X,Y) = \sum _{x<X,y<Y} \texttt{image} (x,y)\]
OutputArray sqsum:对像素值进行平方之后再计算得到的积分图,积分图大小是$(W+1) \times (H+1)$,类型为双精度浮点型(64f)。- \[\texttt{sqsum} (X,Y) = \sum _{x<X,y<Y} \texttt{image} (x,y)^2\]
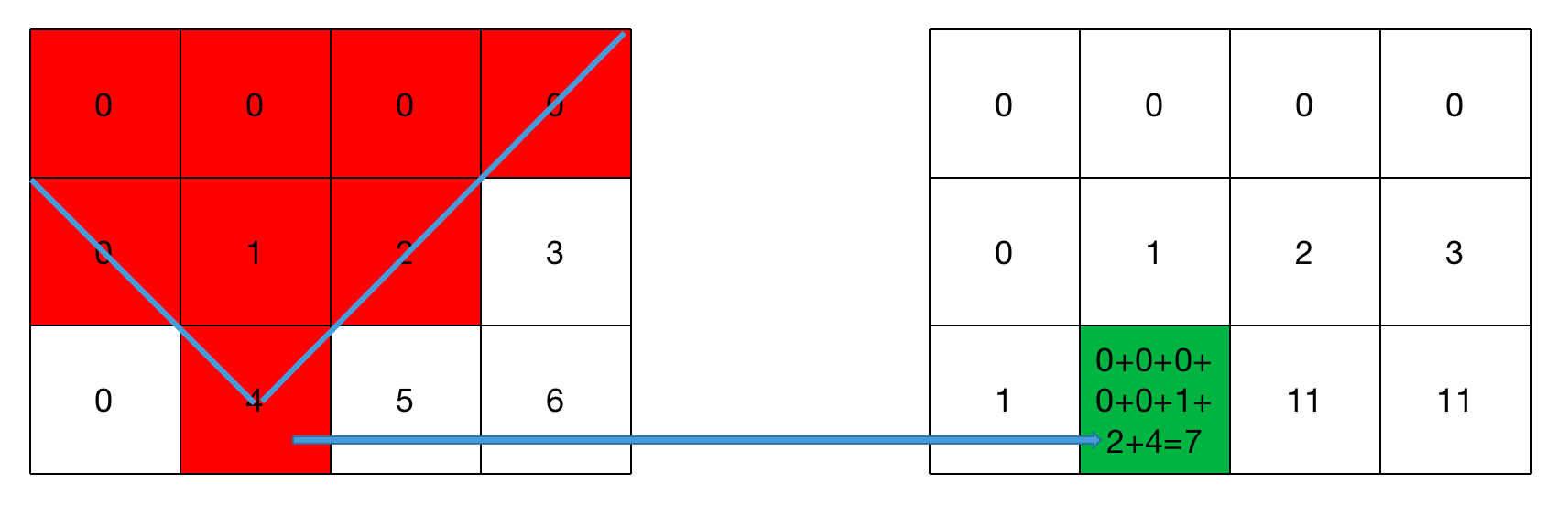
OutputArray tilted:对原始图像旋转45度后再计算得到的积分图,积分图的大小依然是$(W+1) \times (H+1)$,类型和sum一样。- \[\texttt{tilted} (X,Y) = \sum _{y<Y,abs(x-X+1) \leq Y-y-1} \texttt{image} (x,y)\]
int sdepth = -1:sum和tilted的位图深度,可以是CV_32S、CV_32F或CV_64F。int sqdepth = -1:sqsum的位图深度,可以是CV_32F或CV_64F。
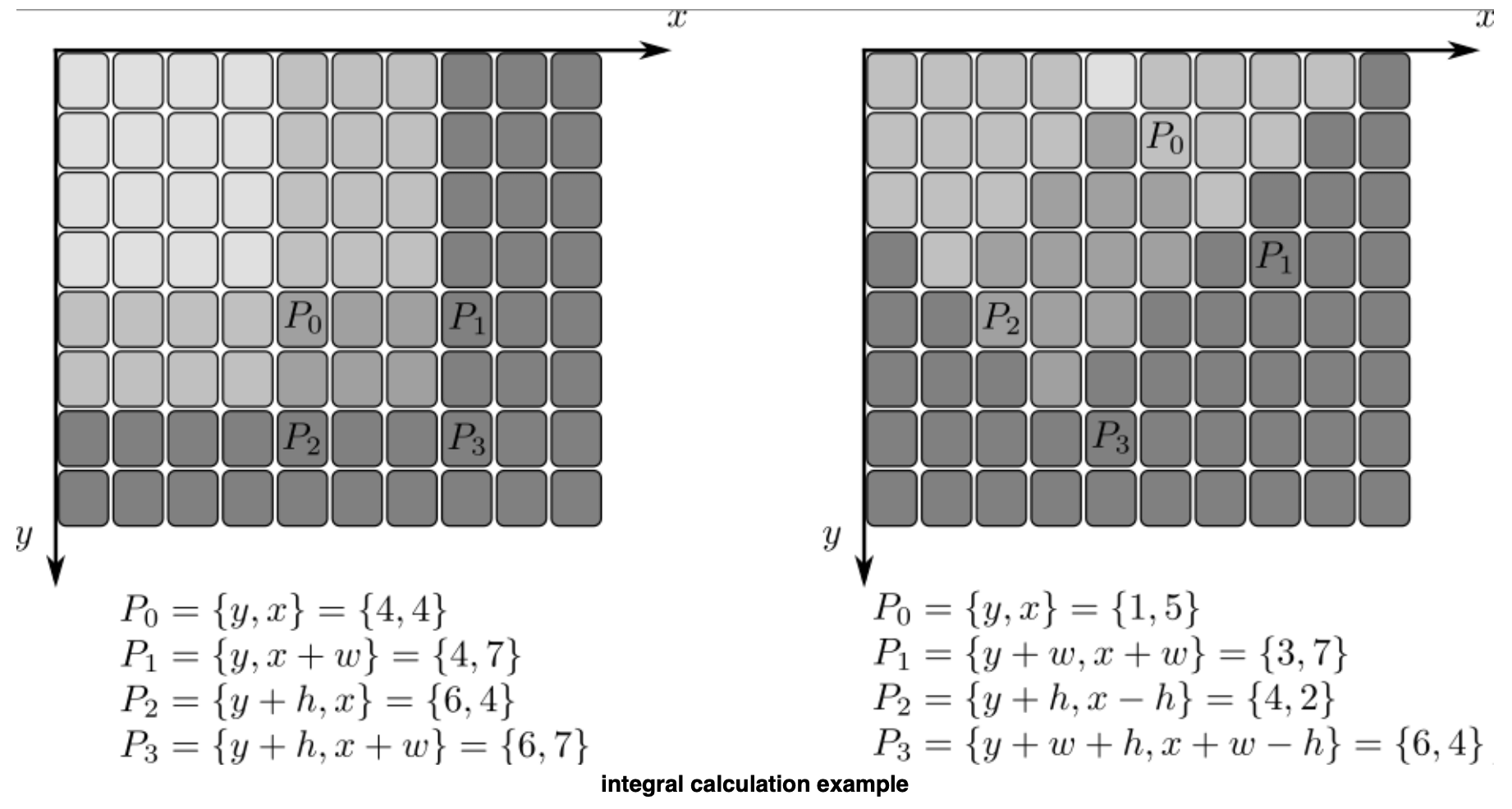
上图是一个例子。上图左是Rect(4,4,3,2)矩形内的积分计算,上图右是一个倾斜矩形Rect(5,1,2,3)内的积分计算。
代码测试:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
Mat src = (Mat_<uchar>(2,3)<<1,2,3,4,5,6);
for(int r =0 ; r<src.rows; r++)
{
for(int c = 0 ; c<src.cols; c++)
{
int i = src.ptr<uchar>(r)[c];
std::cout<<i<<" ";
}
std::cout<<std::endl;
}
/*
1 2 3
4 5 6
*/
for(int r =0 ; r<src.rows; r++)
{
for(int c = 0 ; c<src.cols; c++)
{
int i = src.ptr<uchar>(r)[c];
std::cout<<i*i<<" ";
}
std::cout<<std::endl;
}
/*
1 4 9
16 25 36
*/
Mat sumii = Mat::zeros(src.rows + 1, src.cols + 1, CV_32FC1);
Mat sqsumii = Mat::zeros(src.rows + 1, src.cols + 1, CV_64FC1);
Mat tilt = Mat::zeros(src.rows + 1, src.cols + 1, CV_32FC1);
integral(src, sumii, sqsumii, tilt);
for(int r =0 ; r<sumii.rows; r++)
{
for(int c = 0 ; c<sumii.cols; c++)
{
int i = sumii.ptr<int>(r)[c];//用float或double输出的数值不对
std::cout<<i<<" ";
}
std::cout<<std::endl;
}
/*
0 0 0 0
0 1 3 6
0 5 12 21
*/
for(int r =0 ; r<sqsumii.rows; r++)
{
for(int c = 0 ; c<sqsumii.cols; c++)
{
double i = sqsumii.ptr<double>(r)[c];
std::cout<<i<<" ";
}
std::cout<<std::endl;
}
/*
0 0 0 0
0 1 5 14
0 17 46 91
*/
for(int r =0 ; r<tilt.rows; r++)
{
for(int c = 0 ; c<tilt.cols; c++)
{
int i = tilt.ptr<int>(r)[c];
std::cout<<i<<" ";
}
std::cout<<std::endl;
}
/*
0 0 0 0
0 1 2 3
1 7 11 11
*/
tilt就是计算旋转45度后矩形的面积,比如: