本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
本文基于PaddlePaddle对YOLOv3进行了改进,提出了PP-YOLO。我们使用了一系列几乎不会增加推理时间的技巧来提高模型的整体性能。
和YOLOv4不同,我们没有探索不同的backbone网络以及data augmentation方法,也没有使用NAS来搜索超参数。PP-YOLO使用最常见的ResNet作为backbone。至于data augmentation,我们使用了最基础的MixUp。PP-YOLO的参数设置遵循YOLOv3。
2.Related Work
不再赘述。
3.Method
我们首先修改了YOLOv3的结构,将backbone替换为ResNet50-vd-dcn,并将其作为basic baseline。
3.1.Architecture
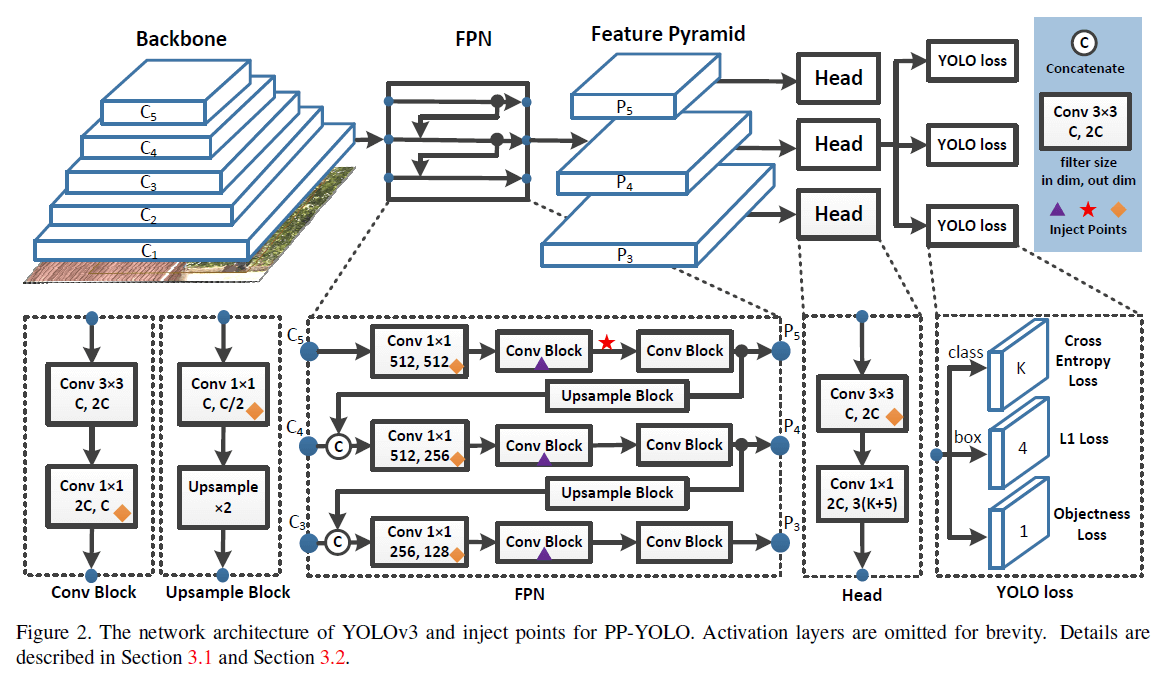
👉Backbone
在PP-YOLO中,我们将YOLOv3中的DarkNet-53替换为了ResNet50-vd。但考虑到直接将DarkNet-53替换为ResNet50-vd会损伤YOLOv3的性能。我们将ResNet50-vd中的一些卷积层修改为了可变卷积层。DCN的有效性在很多检测模型中已经得到了验证。DCN虽然不会显著增加模型的参数量和FLOPs,但在实际实践中,过多的DCN层会大幅提升推理时间。因此,为了平衡效率和性能,我们仅把最后一个stage的$3 \times 3$卷积层替换为了DCN。我们把这个修改后的backbone称为ResNet50-vd-dcn,第3、4、5个stage的输出分别为$C_3,C_4,C_5$。
👉Detection Neck
使用了FPN。$C_3,C_4,C_5$作为FPN的输入,对应的每层输出为$P_3,P_4,P_5$(记为$P_l$,其中$l=3,4,5$)。$P_l$的分辨率为$\frac{W}{2^l} \times \frac{H}{2^l}$,其中,输入图像的大小为$W\times H$。
👉Detection Head
YOLOv3的detection head非常简单。它包含2个卷积层。一个$3 \times 3$卷积后跟一个$1 \times 1$卷积得到最终的预测结果。每个head的输出通道数为$3(K+5)$,其中$K$是类别数。每个最终的预测map中的每个位置都会预测3个不同的anchor。对于每个anchor,前K个通道预测$K$个类别的概率,随后4个通道预测bbox的位置。最后一个通道预测目标分数(个人注解:即存在目标的概率)。各部分使用的loss见Fig2,常规的YOLO loss,在此不再详述。
3.2.Selection of Tricks
我们尝试了很多现有的tricks。
👉Larger Batch Size
使用更大的batch size提升了训练的稳定性,并得到了更好的结果。我们将训练的batch size从64调整到了192,也相应的调整了训练策略和学习率。
👉EMA
使用EMA更新训练参数:
\[W_{EMA} = \lambda W_{EMA} + (1-\lambda)W \tag{1}\]其中,$\lambda$是decay,设为0.9998。
👉DropBlock
DropBlock是一种结构化的DropOut,其feature map中的连续区域一起被drop掉。和原始论文(G. Ghiasi, T.-Y. Lin, and Q. V. Le. Dropblock: A regularization method for convolutional networks. In NeurIPS, 2018.)不同,我们只对FPN部分使用了DropBlock,因为我们发现对backbone使用DropBlock会降低精度。Fig2中的紫色三角就表示使用了DropBlock。
bbox regression是目标检测中的一个重要步骤。在YOLOv3中,bbox regression使用了L1 loss。它不是为mAP评估指标量身定制的,该指标强烈依赖于IoU。和YOLOv4不同,我们没有将L1 loss直接替换为IoU loss,我们额外添加了一个分支用于计算IoU loss。此外,我们还发现各种IoU loss变体的性能都差不多,所以我们使用了最基础的IoU loss(下图取自Unitbox论文):

在YOLOv3中,把类别概率和目标分数相乘作为最终的检测置信度,这并没有考虑到定位的精度。为了解决这一问题,我们添加了一个IoU预测分支来评估定位的精度。在训练阶段,IoU aware loss被用于训练IoU预测分支。在推理阶段,将类别概率、目标分数、预测的IoU,三者的乘积作为最终的检测置信度。然后,最终的检测置信度被用作后续NMS的输入。IoU预测分支会增加额外的计算成本,但只增加了0.01%的参数量和0.0001%的FLOPs,所以增加的计算成本可以被忽略。
IoU预测分支的添加方式可参考下图(取自IoU Aware论文):

👉Grid Sensitive
同YOLOv4,使用了Grid Sensitive。在原始的YOLOv3中,bbox的中心点坐标为:
\[x = s \cdot (g_x + \sigma (p_x)) \tag{2}\] \[y = s \cdot (g_y + \sigma (p_y)) \tag{3}\]其中,$\sigma$是sigmoid函数,$s$是scale factor。Grid Sensitive将其修改为:
\[x = s \cdot (g_x + \alpha \cdot \sigma(p_x) - (\alpha -1)/2) \tag{4}\] \[y=s \cdot (g_y + \alpha \cdot \sigma (p_y)-(\alpha-1)/2) \tag{5}\]本文设$\alpha=1.05$。Grid Sensitive带来的FLOPs增长很小,可以忽略不计。
👉Matrix NMS
Matrix NMS:X. Wang, R. Zhang, T. Kong, L. Li, and C. Shen. Solov2: Dynamic, faster and stronger. arXiv preprint arXiv:2003.10152, 2020.
Soft NMS:Navaneeth Bodla, Bharat Singh, Rama Chellappa, and Larry Davis. Soft-NMS: improving object detection with one line of code. In Proc. IEEE Int. Conf. Comp. Vis., 2017.
首先来解释下Soft NMS(下图来自Soft-NMS论文):

红框是传统的NMS算法,绿框是Soft NMS算法,剩余部分都是一样的。对于传统的NMS算法来说,如果两个目标过于接近,则其中一个目标的检测框可能会被抑制(即置信度被置为0),如下图所示(图片来自Soft-NMS论文):

在上图中,绿色框检测到的马可能会被传统NMS算法所忽视,造成漏检。传统NMS算法可用下式表示:
\[s_i = \begin{cases} s_i, & \text{iou}(\mathcal{M}, b_i) < N_t \\ 0, & \text{iou}(\mathcal{M}, b_i) \geq N_t \end{cases}\]Soft NMS的思路就是不会把重叠面积大于阈值的检测框的置信度直接置为0,而是让其置信度逐渐下降,用公式表示为:
\[s_i = \begin{cases} s_i, & \text{iou}(\mathcal{M}, b_i) < N_t \\ s_i(1-\text{iou}(\mathcal{M},b_i)), & \text{iou}(\mathcal{M}, b_i) \geq N_t \end{cases}\]但在上述公式中,在阈值$N_t$附近,检测框置信度的变化不是连续的,因此,将上述公式进行优化,不考虑阈值,对所有检测框的置信度都进行更新(使用高斯惩罚函数):
\[s_i = s_i e ^{-\frac{\text{iou}(\mathcal{M},b_i)^2}{\sigma}}, \ \forall b_i \notin \mathcal{D}\]个人注解:在Soft NMS中,可以通过设置检测框置信度阈值来对检测框进行筛选。
Matrix NMS基于Soft NMS做了以下几点优化:
- 以全局视角考虑检测框之间的关系,而Soft NMS只考虑了与最大置信度检测框的重叠程度。
- 修改了置信度更新的公式。
- 增加了并行处理,大幅提升了NMS的速度。
Matrix NMS的python代码见下(取自Solov2论文):

因为Solov2论文是分割任务,所以计算的是mask之间的IoU。假设一共有$N$个mask,我们计算其两两之间的IoU,得到一个$N \times N$的IoU矩阵:
\[\text{ious} = \begin{bmatrix} 0 & \text{iou}_{12} & \text{iou}_{13} & \text{iou}_{14} & \cdots & \text{iou}_{1N} \\ 0 & 0 & \text{iou}_{23} & \text{iou}_{24} & \cdots & \text{iou}_{2N} \\ 0 & 0 & 0 & \text{iou}_{34} & \cdots & \text{iou}_{3N} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & 0 \end{bmatrix}\]其中,$\text{iou}_{12}$表示第一个mask和第二个mask的IoU。为了避免重复计算,ious是一个上三角矩阵。ious中每一列的最大值为ious_cmax。置信度衰减有两种计算方法:高斯衰减和线性衰减。
👉CoordConv
R. Liu, J. Lehman, P. Molino, F. P. Such, E. Frank, A. Sergeev, and J. Yosinski. An intriguing failing of convolutional neural networks and the coordconv solution. In NeurIPS, pages 9605–9616, 2018.

如上图(取自CoordConv论文)所示,CoordConv层是在原始卷积的基础上增加了两个通道的输入,分别代表$x$坐标和$y$坐标。$i$坐标通道和$j$坐标通道的大小都是$h \times w$:
\[i\ \text{coordinate} \ \text{channel} = \begin{bmatrix} 0 & 0 & \cdots & 0 \\ 1 & 1 & \cdots & 1 \\ 2 & 2 & \cdots & 2 \\ \vdots & \vdots & \vdots & \vdots \end{bmatrix}_{h \times w}\] \[j\ \text{coordinate} \ \text{channel} = \begin{bmatrix} 0 & 1 & 2 & \cdots \\ 0 & 1 & 2 & \cdots \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 1 & 2 & \cdots \end{bmatrix}_{h \times w}\]在实际使用中,会将$i,j$归一化到$[-1,1]$。甚至在一些情况下,我们可以再添加一个通道用于$r$坐标,其中,
\[r = \sqrt{(i-h/2)^2+(j-w/2)^2}\]卷积层有3个特性:1)可学习参数相对较少;2)在GPU上计算速度很快;3)具有平移不变性。CoordConv层保留了前两个特性,允许网络根据学习任务的需要,自行选择保留或舍弃第三个特性——平移不变性。
在PP-YOLO中,考虑到CoordConv会增加一些参数和FLOPs,因此只将FPN中的$1\times 1$卷积层和detection head中的第一个卷积层替换为CoordConv。在Fig2中,用黄色菱形表示使用了CoordConv。
👉SPP
在Fig2中,红色五星表示使用了SPP。SPP本身并没有引入额外的参数,但是会增加下一个卷积层的输入通道数量。所以最终,增加了2%左右的参数量和1%的FLOPs。
👉Better Pretrain Model
使用一个在ImageNet上分类精度更高的预训练模型有助于提升其检测性能。我们这里使用一个蒸馏过的ResNet50-vd作为预训练模型(见:Introduction of model compression methods)。
4.Experiment
在COCO数据集上进行实验,使用trainval35k作为训练集(约118k张图像),使用minival作为验证集(约5k张图像),使用test-dev作为测试集(约20k张图像)。
4.1.Implementation Details
除非特殊说明,都使用ResNet50-vd-dcn作为backbone。我们基础模型的FPN以及head和YOLOv3是一模一样的。backbone网络用在ImageNet上的预训练权重进行初始化。对于FPN和detection head,使用随机初始化,这和YOLOv3是一样的。在larger batch size设置下,使用SGD训练了250K次迭代,初始学习率为0.01,minibatch size=192,使用了8块GPU。多尺度训练从320个像素到608个像素。MixUp用于data augmentation。
4.2.Ablation Study

4.3.Comparison with Other State-of-the-Art Detectors

在Fig1中,每条线上的4个节点表示不同的输入大小,分别为320、416、512、608。

5.Conclusions
不再赘述。
6.原文链接
👽PP-YOLO:An Effective and Efficient Implementation of Object Detector