【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.未标记样本
我们有训练样本集$D_l = \{ (\mathbf{x}_1,y_1), (\mathbf{x}_2,y_2),…,(\mathbf{x}_l,y_l) \}$,这$l$个样本的类别标记(即是否好瓜)已知,称为“有标记”(labeled)样本;此外,还有$D_u = \{ \mathbf{x}_{l+1},\mathbf{x}_{l+2},…,\mathbf{x}_{l+u} \},l \ll u$,这$u$个样本的类别标记未知(即不知是否好瓜),称为“未标记”(unlabeled)样本。若直接使用传统监督学习技术,则仅有$D_l$能用于构建模型,$D_u$所包含的信息被浪费了;另一方面,若$D_l$较小,则由于训练样本不足,学得模型的泛化能力往往不佳。那么,能否在构建模型的过程中将$D_u$利用起来呢?
一个简单的做法,是将$D_u$中的示例全部标记后用于学习。这就相当于请瓜农把地里的瓜全都检查一遍,告诉我们哪些是好瓜,哪些不是好瓜,然后再用于模型训练。显然,这样做需耗费瓜农大量时间和精力。有没有“便宜”一点的办法呢?
我们可以用$D_l$先训练一个模型,拿这个模型去地里挑一个瓜,询问瓜农好不好,然后把这个新获得的有标记样本加入$D_l$中重新训练一个模型,再去挑瓜,$\cdots \cdots$这样,若每次都挑出对改善模型性能帮助大的瓜,则只需询问瓜农比较少的瓜就能构建出比较强的模型,从而大幅降低标记成本。这样的学习方式称为“主动学习”(active learning),其目标是使用尽量少的“查询”(query)来获得尽量好的性能(即尽量少向瓜农询问)。
例如基于$D_l$训练一个SVM,挑选距离分类超平面最近的未标记样本来进行查询。
显然,主动学习引入了额外的专家知识,通过与外界的交互来将部分未标记样本转变为有标记样本。若不与专家交互,没有获得额外信息,还能利用未标记样本来提高泛化性能吗?答案是可以。
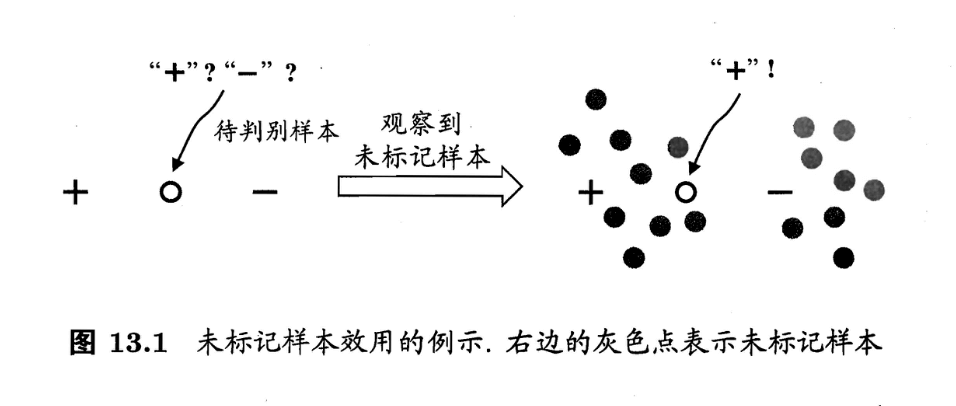
事实上,未标记样本虽未直接包含标记信息,但若它们与有标记样本是从同样的数据源独立同分布采样而来,则它们所包含的关于数据分布的信息对建立模型将大有裨益。图13.1给出了一个直观的例示。若仅基于图中的一个正例和一个反例,则由于待判别样本恰位于两者正中间,大体上只能随机猜测;若能观察到图中的未标记样本,则将很有把握地判别为正例。
让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能,就是半监督学习(semi-supervised learning)。半监督学习的现实需求非常强烈,因为在现实应用中往往能容易地收集到大量未标记样本,而获取“标记”却需耗费人力、物力。
要利用未标记样本,必然要做一些将未标记样本所揭示的数据分布信息与类别标记相联系的假设。最常见的是“聚类假设”(cluster assumption),即假设数据存在簇结构,同一个簇的样本属于同一个类别。图13.1就是基于聚类假设来利用未标记样本,由于待预测样本与正例样本通过未标记样本的“撮合”聚在一起,与相对分离的反例样本相比,待判别样本更可能属于正类。半监督学习中另一种常见的假设是“流形假设”(manifold assumption),即假设数据分布在一个流形结构上,邻近的样本拥有相似的输出值。“邻近”程度常用“相似”程度来刻画,因此,流形假设可看作聚类假设的推广,但流形假设对输出值没有限制,因此比聚类假设的适用范围更广,可用于更多类型的学习任务。事实上,无论聚类假设还是流形假设,其本质都是“相似的样本拥有相似的输出”这个基本假设。
聚类假设考虑的是类别标记,通常用于分类任务。
半监督学习可进一步划分为纯(pure)半监督学习和直推学习(transductive learning),前者假定训练数据中的未标记样本并非待预测的数据,而后者则假定学习过程中所考虑的未标记样本恰是待预测数据,学习的目的就是在这些未标记样本上获得最优泛化性能。换言之,纯半监督学习是基于“开放世界”假设,希望学得模型能适用于训练过程中未观察到的数据;而直推学习是基于“封闭世界”假设,仅试图对学习过程中观察到的未标记数据进行预测。图13.2直观地显示出主动学习、纯半监督学习、直推学习的区别。需注意的是,纯半监督学习和直推学习常合称为半监督学习。
