【机器学习基础】系列博客为参考周志华老师的《机器学习》一书,自己所做的读书笔记。
本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.半监督SVM
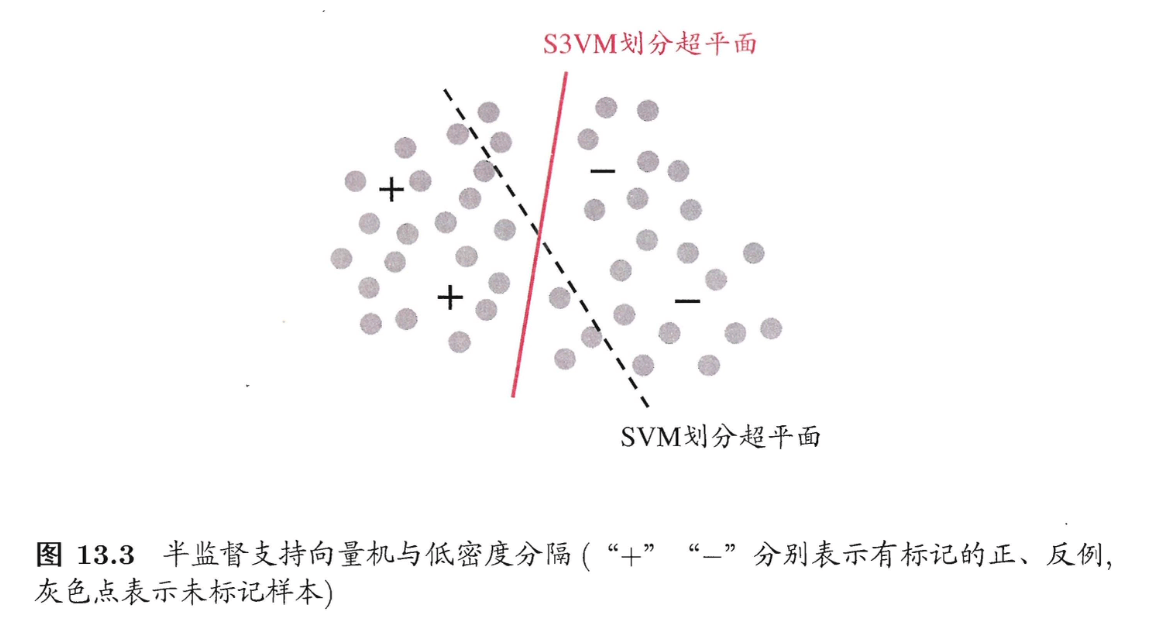
半监督支持向量机(Semi-Supervised Support Vector Machine,简称S3VM)是支持向量机在半监督学习上的推广。在不考虑未标记样本时,支持向量机试图找到最大间隔划分超平面,而在考虑未标记样本后,S3VM试图找到能将两类有标记样本分开,且穿过数据低密度区域的划分超平面,如图13.3所示,这里的基本假设是“低密度分隔”(low-density separation),显然,这是聚类假设在考虑了线性超平面划分后的推广。
半监督支持向量机中最著名的是TSVM(Transductive Support Vector Machine)。与标准SVM一样,TSVM也是针对二分类问题的学习方法。TSVM试图考虑对未标记样本进行各种可能的标记指派(label assignment),即尝试将每个未标记样本分别作为正例或反例,然后在所有这些结果中,寻求一个在所有样本(包括有标记样本和进行了标记指派的未标记样本)上间隔最大化的划分超平面。一旦划分超平面得以确定,未标记样本的最终标记指派就是其预测结果。
形式化地说,给定$D_l = \{ (\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_l,y_l) \}$和$D_u = \{ \mathbf{x}_{l+1},\mathbf{x}_{l+2},…,\mathbf{x}_{l+u} \}$,其中$y_i \in \{-1,+1 \}, l \ll u, l+u=m$(符号定义见:【机器学习基础】第五十七课:[半监督学习]生成式方法)。TSVM的学习目标是为$D_u$中的样本给出预测标记$\hat{\mathbf{y}}=(\hat{y}_{l+1},\hat{y}_{l+2},…,\hat{y}_{l+u}),\hat{y}_i\in \{-1,+1 \}$,使得:
\[\begin{align*} \min_{\mathbf{w},b,\hat{\mathbf{y}},\xi} \quad & \frac{1}{2} \|\mathbf{w}\|_2^2 + C_l \sum_{i=1}^{l} \xi_i + C_u \sum_{i=l+1}^{m} \xi_i \\ \text{s.t.} \quad & y_i(\mathbf{w}^T\mathbf{x}_i+b) \geq 1 - \xi_i, \quad i=1,2,\dots,l, \\ & \hat{y}_i(\mathbf{w}^T\mathbf{x}_i+b) \geq 1 - \xi_i, \quad i=l+1,l+2,\dots,m, \\ & \xi_i \geq 0, \quad i=1,2,\dots,m. \end{align*} \tag{1}\]下式可参考:【机器学习基础】第十九课:支持向量机之软间隔与正则化。
其中,$(\mathbf{w},b)$确定了一个划分超平面;$\xi$为松弛向量,$\xi_i (i=1,2,…,l)$对应于有标记样本,$\xi_i (i=l+1,l+2,…,m)$对应于未标记样本;$C_l$与$C_u$是由用户指定的用于平衡模型复杂度、有标记样本与未标记样本重要程度的折中参数。
显然,尝试未标记样本的各种标记指派是一个穷举过程,仅当未标记样本很少时才有可能直接求解。在一般情况下,必须考虑更高效的优化策略。
TSVM采用局部搜索来迭代地寻找式(1)的近似解。具体来说,它先利用有标记样本学得一个SVM,即忽略式(1)中关于$D_u$与$\hat{\mathbf{y}}$的项及约束。然后,利用这个SVM对未标记数据进行标记指派(label assignment),即将SVM预测的结果作为“伪标记”(pseudo-label)赋予未标记样本。此时$\hat{\mathbf{y}}$成为已知,将其代入式(1)即得到一个标准SVM问题,于是可求解出新的划分超平面和松弛向量;注意到此时未标记样本的伪标记很可能不准确,因此$C_u$要设置为比$C_l$小的值,使有标记样本所起作用更大。接下来,TSVM找出两个标记指派为异类且很可能发生错误的未标记样本,交换它们的标记,再重新基于式(1)求解出更新后的划分超平面和松弛向量,然后再找出两个标记指派为异类且很可能发生错误的未标记样本,$\cdots \cdots$标记指派调整完成后,逐渐增大$C_u$以提高未标记样本对优化目标的影响,进行下一轮标记指派调整,直至$C_u = C_l$为止。此时求解得到的SVM不仅给未标记样本提供了标记,还能对训练过程中未见的示例进行预测。TSVM的算法描述如图13.4所示。

在对未标记样本进行标记指派及调整的过程中,有可能出现类别不平衡问题,即某类的样本远多于另一类,这将对SVM的训练造成困扰。为了减轻类别不平衡性所造成的不利影响,可对图13.4的算法稍加改进:将优化目标中的$C_u$项拆分为$C_u^+$与$C_u^-$两项,分别对应基于伪标记而当作正、反例使用的未标记样本,并在初始化时令
\[C_u^+ = \frac{u_-}{u_+} C_u^- \tag{2}\]其中$u_+$与$u_-$为基于伪标记而当作正、反例使用的未标记样本数。
在图13.4算法的第6-10行中,若存在一对未标记样本$\mathbf{x}_i$与$\mathbf{x}_j$,其标记指派$\hat{y}_i$与$\hat{y}_j$不同,且对应的松弛变量满足$\xi_i+\xi_j > 2$,则意味着$\hat{y}_i$与$\hat{y}_j$很可能是错误的,需对二者进行交换后重新求解式(1),这样每轮迭代后均可使式(1)的目标函数值下降。
显然,搜寻标记指派可能出错的每一对未标记样本进行调整,是一个涉及巨大计算开销的大规模优化问题。因此,半监督SVM研究的一个重点是如何设计出高效的优化求解策略,由此发展出很多方法,如基于图核(graph kernel)函数梯度下降的LDS、基于标记均值估计的meanS3VM等。