本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.背景(Introduction)
自LeNet之后,卷积神经网络越来越受到人们的关注并且取得了相当不错的成绩。ZFNet作者认为原因有三:1)带有标记的训练集越来越多,数据量越来越大;2)GPU性能的提升,使得训练大型神经网络成为可能;3)更好的正则化方法,例如Dropout。
被称为ZFNet的原因在于两位作者的名字:Zeiler、Fergus。
尽管卷积神经网络取得了如此令人振奋的进展,但对于这些复杂模型内部的操作和行为,以及它们是如何取得如此好的性能,仍然缺乏深入的了解。如果我们不能从本质上了解卷积神经网络起效的原因,那么其未来的发展就只能基于以往的经验进行尝试,这对于卷积神经网络的发展是不利的。因此,ZFNet作者提出了一种可视化方法,用于揭示输入是如何激活每一个隐藏层的。通过这种可视化方式,使得我们可以评估feature在网络前向传播中的演变过程并且可以发现模型中可能存在的潜在问题。可视化是通过一个多层反卷积网络(deconvnet)实现的。此外,作者还通过对输入进行部分遮挡来测试哪些部分对于分类结果更为重要。
ZFNet在ILSVRC2013的分类任务中取得了季军的好成绩,分类任务的前两名为Clarifai和NUS:
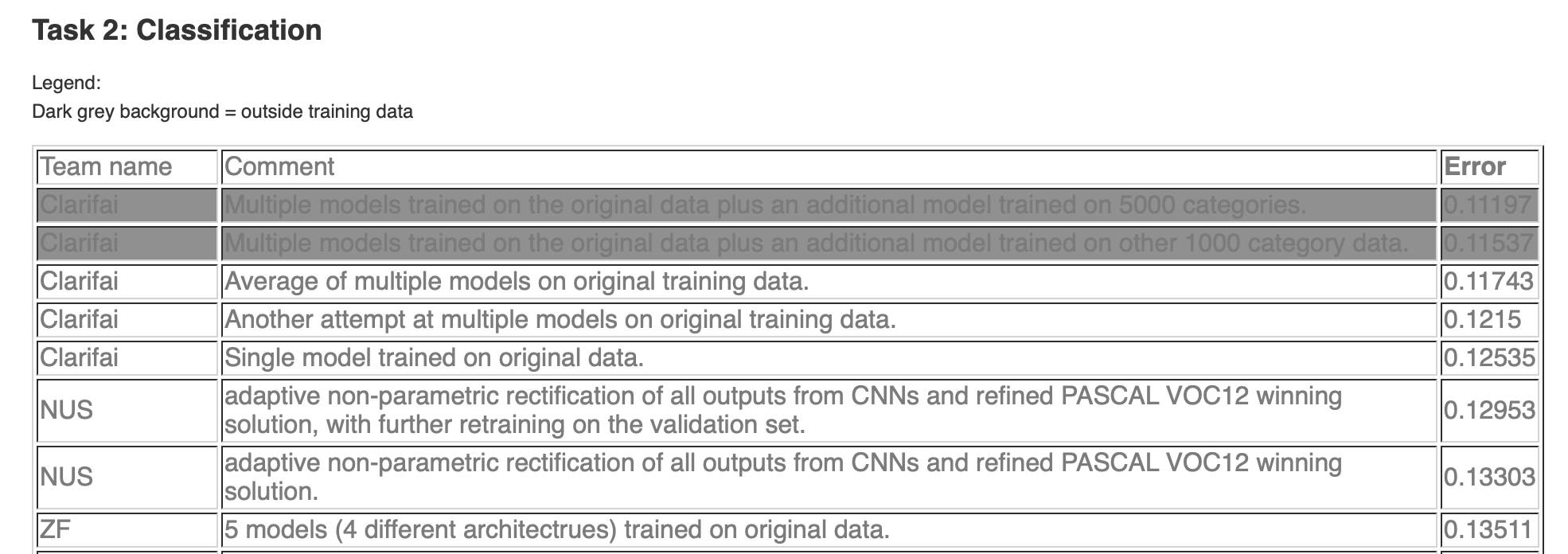
ILSVRC2013成绩查询地址:🔗链接
1.1.相关工作(Related Work)
通过可视化feature来了解网络是一种很常见的方法,但是通常都只局限在第一层。在本小节中,作者列举了其他文献所用方法的缺点和限制,在此不再赘述。
2.方法(Approach)
ZFNet使用像LeNet、AlexNet那样的标准的卷积神经网络结构。ZFNet和LeNet、AlexNet一样,输入($x_i$)为2D的彩色图像,经过一系列隐藏层后,得到的输出($\hat y_i$)为每一个类别的概率(共有$C$个类别)。每一层都包括:1)通过filters对上一层的输出(即该层的输入)进行卷积操作(除了第一层,其输入为图像);2)ReLU激活函数;3)[可选]max-pooling;4)[可选]局部对比度归一化(Local Contrast Normalization,LCN)。
LCN出自论文:Jarrett, K., Kavukcuoglu, K., Ranzato, M., and Le-Cun, Y. What is the best multi-stage architecture for object recognition? In ICCV, 2009.
文中对LCN的解释见下:
LCN类似于均值-标准差归一化。第$i$个feature map中,坐标为$(j,k)$的点的值为$x_{i,j,k}$。首先,去均值化(减法运算部分):$v_{i,j,k}=x_{i,j,k}-\sum_{ipq} w_{pq} \cdot x_{i,j+p,k+q}$。其中,$w_{pq}$为$p \times q$大小的window上对应位置的高斯系数(所以此处应该用的是二维高斯分布,该论文中使用的window大小为$9\times 9$),且有$\sum_{i,p,q} w_{pq}=1$。然后,除法运算部分:$y_{i,j,k}=v_{i,j,k} / \max(c,\sigma_{jk})$。其中,$\sigma_{jk}=(\sum_{ipq}w_{pq}\cdot v^2_{i,j+p,k+q})^{1/2}$,即标准差;$c=mean(\sigma _{jk})$。
ZFNet网络结构见Fig3:
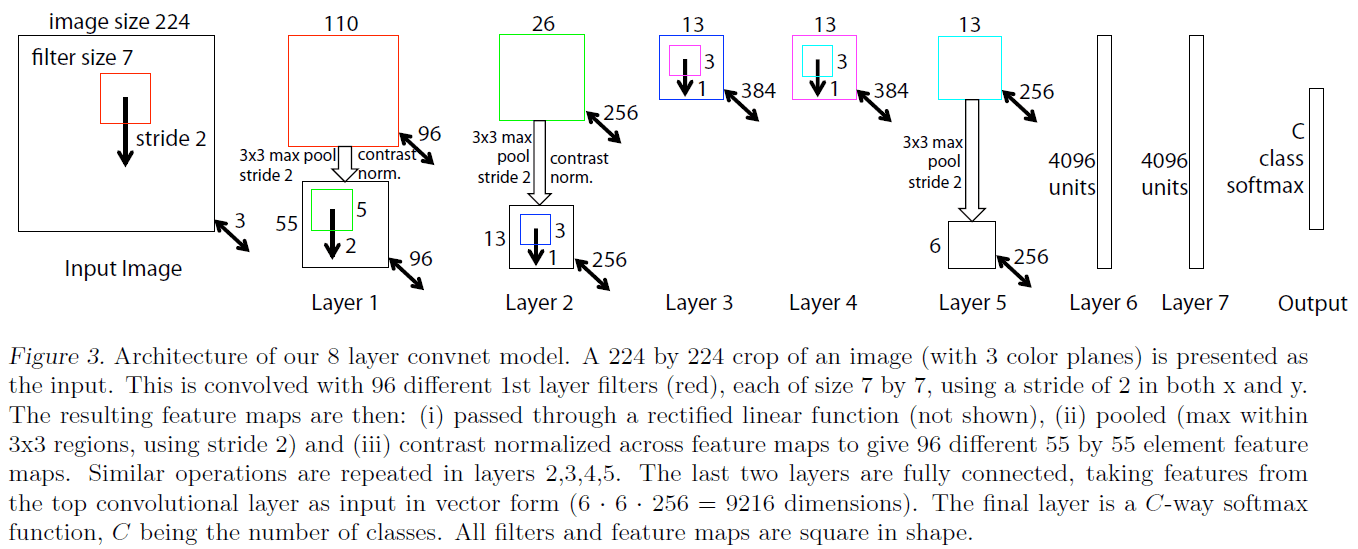
ZFNet共有8层。输入为$224\times 224 \times 3$的彩色图像(输入是从原始图像中裁剪得来的)。
- Layer1
- CONV1:卷积核大小为$7 \times 7 \times 3$,卷积核数量为96,步长为2。如果不做padding,得到的输出应该是$109 \times 109 \times 96$,因此推测此处应该有padding=1,这样输出的维度为$110 \times 110 \times 96$。激活函数为ReLU。此外,其输出需进行LCN处理。
- POOL1:pooling方式为max-pooling,窗口大小为$3\times 3$,步长为2。输出大小为$55\times 55 \times 96$(推测此处有padding=1)。
- Layer2
- CONV2:卷积核大小为$5\times 5 \times 96$,卷积核数量为256,步长为2。输出大小为$26\times 26 \times 256$(推测此处有padding=0)。激活函数为ReLU。CONV2的输出也做了LCN处理。
- POOL2:pooling方式为max-pooling,窗口大小为$3\times 3$,步长为2。输出大小为$13\times 13 \times 256$(推测此处有padding=1)。
- Layer3
- CONV3:卷积核大小为$3\times 3 \times 256$,卷积核数量为384,步长为1。输出大小为$13\times 13 \times 384$(推测此处有padding=1)。激活函数为ReLU。
- Layer4
- CONV4:卷积核大小为$3\times 3 \times 384$,卷积核数量为384,步长为1。输出大小为$13\times 13 \times 384$(推测此处有padding=1)。激活函数为ReLU。
- Layer5
- CONV5:卷积核大小为$3\times 3 \times 384$,卷积核数量为256,步长为1。输出大小为$13\times 13 \times 256$(推测此处有padding=1)。激活函数为ReLU。
- POOL5:pooling方式为max-pooling,窗口大小为$3\times 3$,步长为2。输出大小为$6\times 6 \times 256$(推测此处有padding=0)。
- Layer6
- FC6:4096个神经元。
- Layer7
- FC7:4096个神经元。
- Layer8
- Output:共有C个神经元,即C个类别。激活函数为softmax。
feature map和filter都是正方形。
ZFNet在网络结构方面没有什么创新,基本和AlexNet一样。主要区别是ZFNet将第1层的卷积核大小从$11\times 11$缩小到$7 \times 7$,stride从4改为2。
假设训练集共有$N$张图片${x,y}$,标签为$y_i$,预测结果为$\hat y_i$。ZFNet模型使用交叉熵代价函数。模型训练方法为MBGD。
2.1.通过反卷积网络进行可视化(Visualization with a Deconvnet)
ZFNet的作者提出了反卷积网络的概念用于研究卷积网络的可视化。反卷积网络可以看作是卷积网络的逆向过程。反卷积网络是一种无监督学习,它不具备学习能力,它只是对已经训练好的卷积网络的探索。
反卷积网络的每一层是和卷积网络一一对应的,最终映射回输入图像上。

如Fig1上半部分所示:右边是卷积网络中的一层,左边是对应的反卷积网络中的一层。先看上半部分的右边,对上一层的输出(即本层的输入,对应图中的“Layer Below Pooled Maps”)进行卷积操作(对应图中的“Convolutional Filtering {$F$}”),得到Feature Maps,经过ReLU激活函数(“Rectified Linear Function”)得到Rectified Feature Maps,最后通过Max Pooling,得到该层的输出:Pooled Maps。然后再来看上半部分的左边,先是对该层的输入(“Layer Above Reconstruction”)进行一个Max Unpooling操作,得到Unpooled Maps,然后同样是经过ReLU激活函数得到Rectified Unpooled Maps,最后通过卷积操作(“Convolutional Filtering {$F^T$}”)得到该层的输出(“Reconstruction”)。
可以很容易看到,对一个层进行反卷积,共有三步:1)unpool;2)rectify;3)filter。下面分别来介绍这三个步骤。
👉Unpooling:unpooling的过程见Fig1的下半部分(只考虑max-pooling)。在卷积网络进行max-pooling时,每个pooling区域的最大位置会被记录,即“Switches”。在进行unpooling操作时,将每个最大值恢复到原来的位置上(个人猜测:其余位置赋为0)。
👉Rectification:这部分很简单,就是将Unpooled Maps通过ReLU激活函数。和对应的卷积网络保持一致。
👉Filtering:反卷积网络中使用的卷积核是对应卷积网络中卷积核的转置。使用该卷积核对Rectified Unpooled Maps进行卷积运算,即反卷积操作,或称转置卷积。
‼️反卷积操作:
先来看下正向的卷积操作(将卷积核以及每个卷积窗口内的元素都转换成行向量或列向量表示):
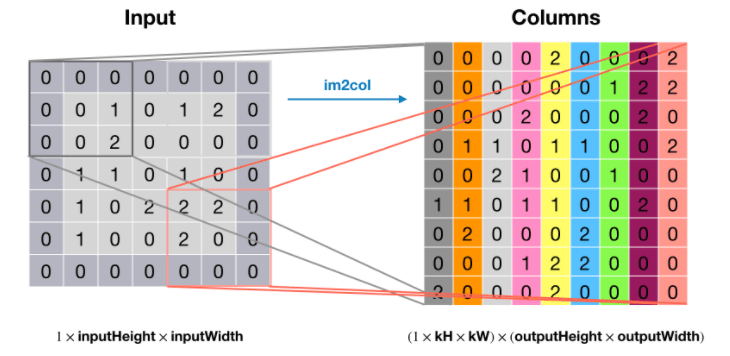
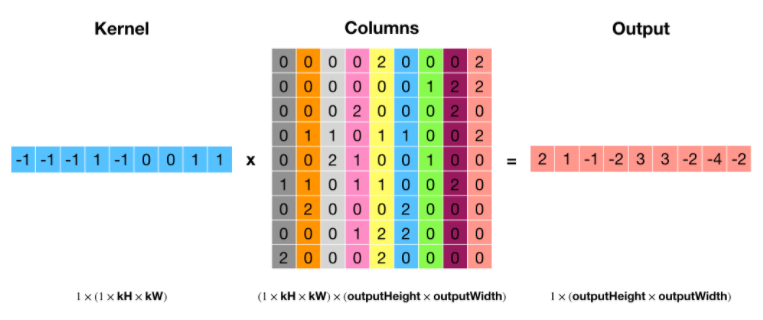
然后是反卷积操作,将卷积核转置:
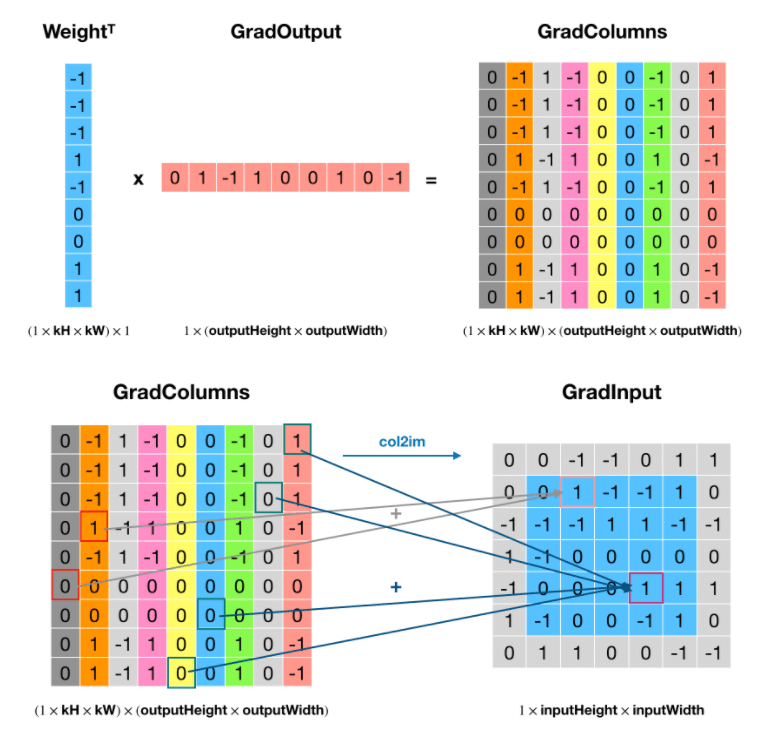
对卷积核进行转置就相当于是对其进行水平和垂直翻转:
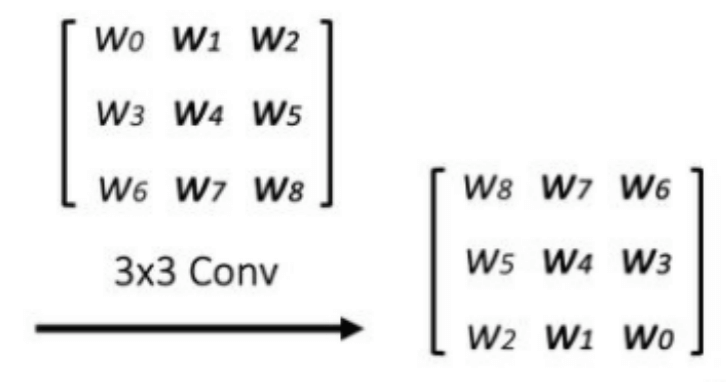
其他维度的反卷积操作以此类推,不再赘述。
3.训练细节(Training Details)
训练所使用的数据集为ImageNet2012提供的训练集(共130万张图像,超过1000个类别)。将数据集中的图像统一resize为$256 \times 256$大小(resize方法和AlexNet一样,请见:链接)。并且每个像素点都减去了其平均值(图像中某一点的像素值的平均值为数据集中所有图像在该点的像素值的平均)。此外,在$256 \times 256$的图像中,ZFNet作者进一步裁剪出$224 \times 224$大小的图像作为网络的输入。一张$256 \times 256$的图像可以得到10张$224 \times 224$大小的图像(四个角+中心便可得到5张,然后进行水平翻转,又可以得到5张,共10张)。训练方法为Mini-Batch+Momentum梯度下降法,其中batch size=128,学习率为$10^{-2}$,Momentum梯度下降法的超参数$\beta$为0.9。当验证集的错误率不再下降时,会手动降低学习率。FC6和FC7使用了dropout,参数为0.5。所有权重初始化为$10^{-2}$,偏置项初始化为0。
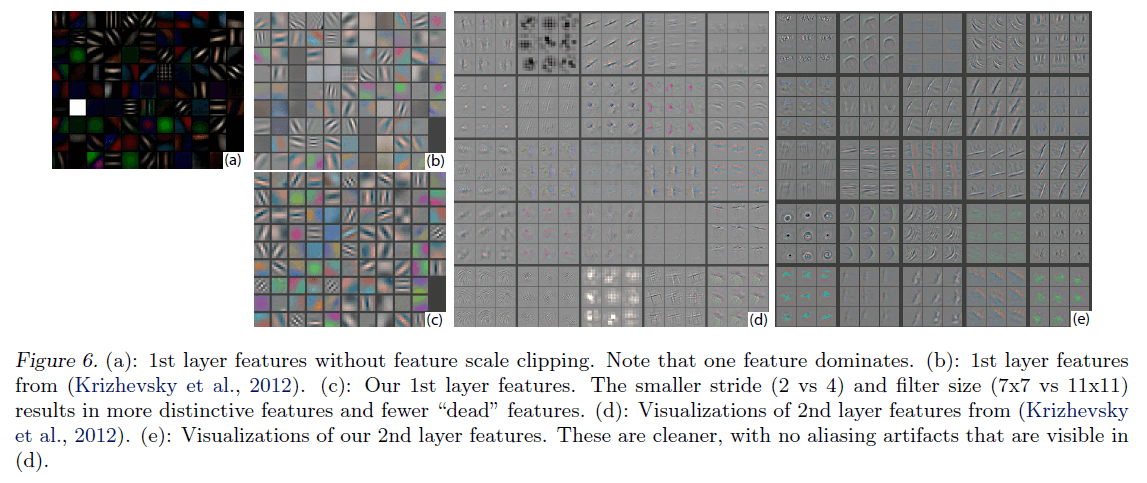
从Fig6(a)的可视化结果可以看出,第一层中有些激活值占据主导地位(即可视化后为白色方块,个人理解:什么特征都没有学习到),为了解决这个问题,ZFNet作者将卷积层中RMS超过$10^{-1}$的filter进行了重新归一化。作者强调这一步很重要,尤其是对于第一层(从Fig6(c)能看到确实有改善)。此外,和AlexNet类似,ZFNet作者也通过裁剪和翻转来扩充训练集。一共训练了70个epoch,在GTX580 GPU上共训练了大约12天。
4.卷积网络的可视化(Convnet Visualization)
使用反卷积网络可视化ImageNet验证集中的激活值(feature activations)。
Feature Visualization:

可视化基于已经训练好的模型。在Fig2中,作者主要展示了两部分内容:1)最能激活某一激活值的9张图片。即这九张图片在训练好的卷积神经网络中,在该激活值处可以取到最大的9个值。2)将某一层进行可视化,然后截取某一激活值映射回输入(也就是二维图像,即pixel space)的部分(the corresponding image patches)用于展示该激活值学到的特征。
在Fig2中,Layer1选择了9个位置的激活值(或者称“特征值”),以及每个位置对应的最能激活该值的9张图片(但是只列出了其中一张图片对应的激活值的可视化结果)。Layer2选择了16个位置的激活值,并且把每一张图片对应的激活值的可视化结果都展示了出来。类似的,Layer3选择了12个位置的激活值,Layer4-Layer5选择了10个位置的激活值。
从Fig2的可视化结果中,我们可以得到很多信息,例如:在Layer5的第一行第二列中,该特征值学到的东西集中在背景的草坪上,而不在前景目标中。此外,不同层数的特征值学到的内容也不同(例如Layer2学到的基本都是简单的几何信息),并且随着层数的加深,特征值学到的内容也在变得复杂。每个特征值对应的9张图片都有很强的关联性。
Feature Evolution during Training:

如图4所示,对Layer1~Layer5中随机选取的6个激活值进行可视化(可视化方法同上,选择训练集中最能激活该激活值的图片)。每个block共有6行,代表着6个激活值,每一行共有8列,代表着训练的不同阶段,分别为epoch=[1,2,5,10,20,30,40,64]。颜色对比度被人为增强用于更好的展示可视化结果。
从图4中可以发现,较浅的层学到的特征收敛的更快。而更深的层则需要训练至少40~50个epoch才能看到特征的收敛。因此,在日常训练卷积神经网络时,我们可以借用此方法来确定一个合适的epoch次数,以确保模型至少训练到特征收敛的程度。
Feature Invariance:
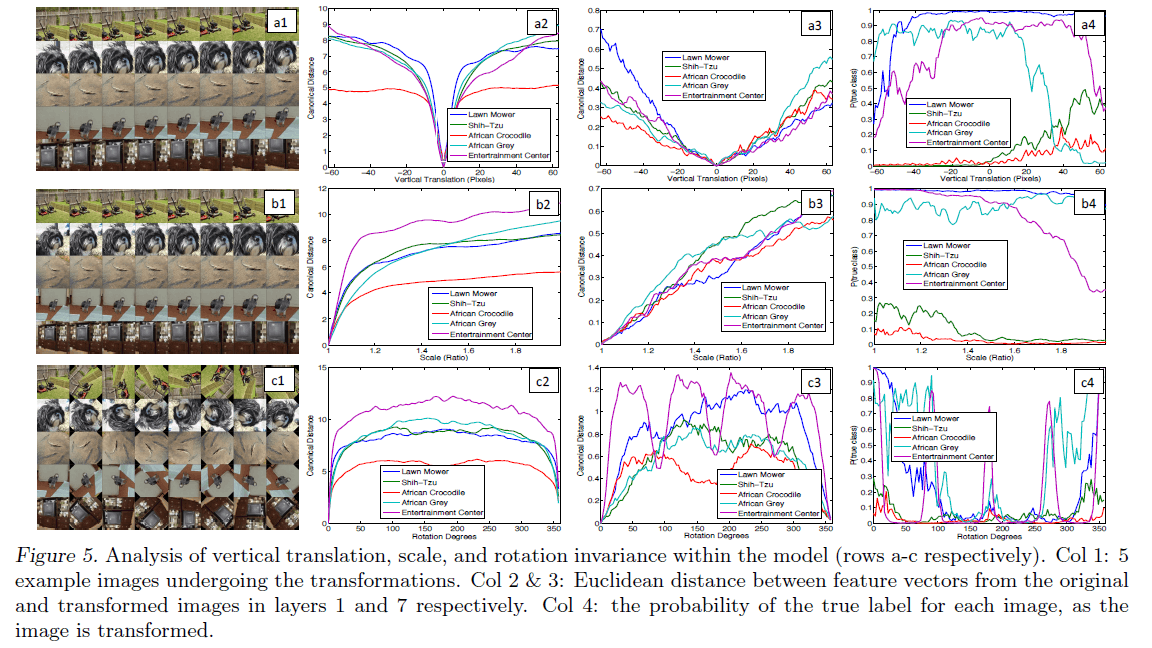
这一部分讨论平移(垂直方向)、缩放以及旋转对特征的影响。Fig5中共有4列:1)第1列是对5张原始图像分别做平移(a1)、缩放(b1)和旋转(c1)处理;2)第2列和第3列图表中的纵轴是图像处理后得到的特征和处理前得到的特征的欧式距离,横轴分别为垂直平移的像素个数、缩放比例、旋转角度。其中,第2列为Layer1的结果,第3列为Layer7的结果;3)第4列中图表的纵轴为预测的图片类别的概率,横轴和第2,3列相同。
对于小幅度的垂直平移和较小程度的缩放,其对Layer1的影响很大,但是对Layer7的影响就小了很多,并且,模型的预测结果也相对稳定。但是对于旋转变化,即使是小角度的旋转,输出结果依旧很不稳定。
4.1.框架选择(Architecture Selection)
可视化可以帮助我们更好的选择模型的参数。在Fig6中,通过可视化AlexNet的Layer1(Fig6(b))和Layer2(Fig6(d)),发现选择更小的卷积核($11\times 11$改为$7\times 7$)和步长(4改为2)可以更好的提取特征,结果见ZFNet的Layer1(Fig6(c))和Layer2(Fig6(e))的可视化结果。并且最终的测试结果也证明这次改动是有助于提升模型性能的。
4.2.遮挡敏感度(Occlusion Sensitivity)
对于图像分类任务来说,人们会很自然的想到一个问题:模型在对图像分类的时候是否真的识别出了目标的位置,还是只利用目标周围的信息进行判断的。ZFNet的作者通过使用灰色块遮挡图像中的不同区域来尝试回答这个问题,结果见Fig7:
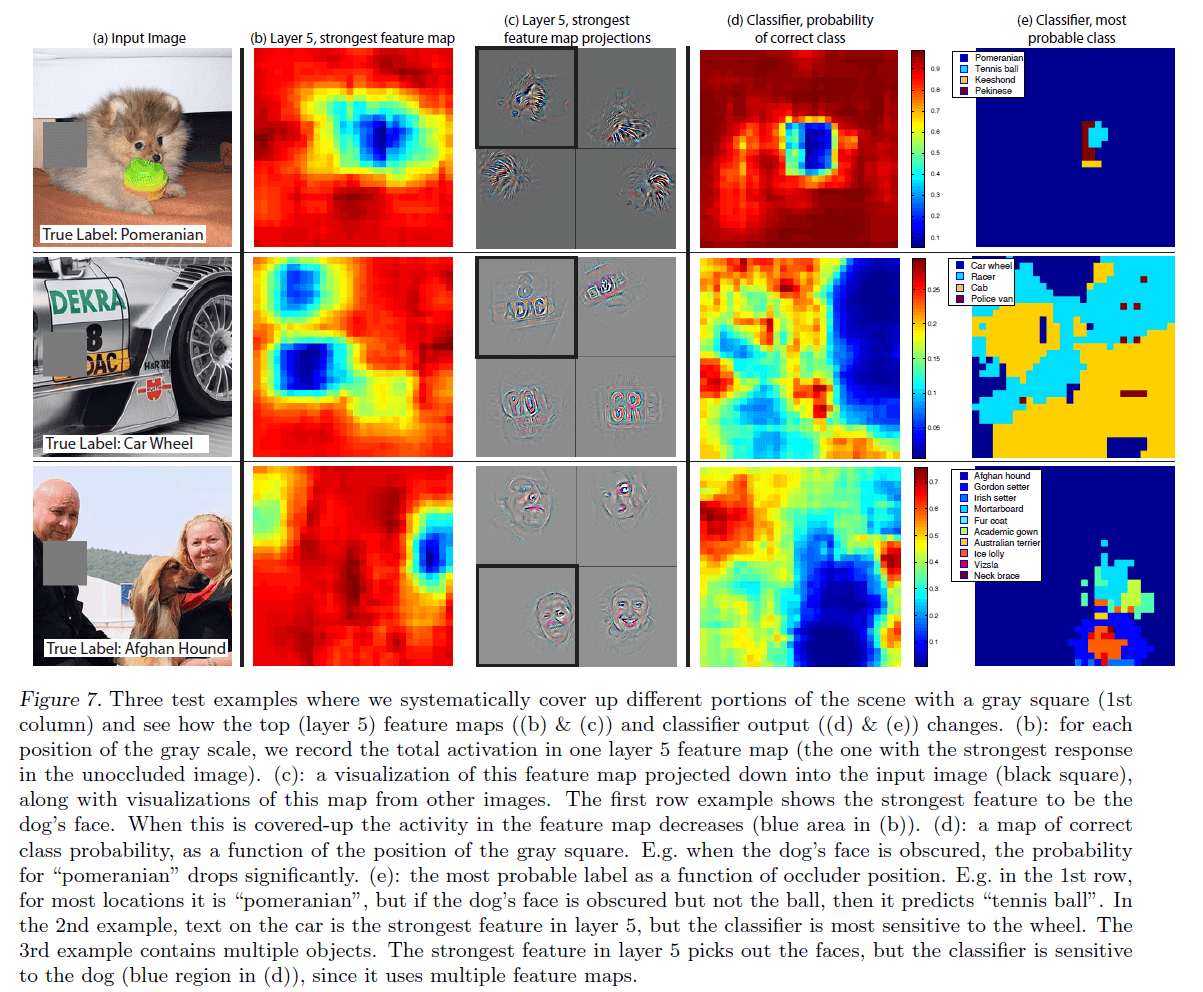
在Fig7中:
- 第一列为分别输入的三张图像,图像的真实类别依次为:博美犬、车轮、阿富汗猎犬。
- 第二列的结果是怎么得到的:首先将未被遮挡的图像输入网络,找到其在Layer5中取到最大激活值所在的feature map(假设记为fm1),然后将灰色块从图像的左上角一直遍历滑动到右下角(就像卷积核的移动方式一样),将每一次滑动得到的fm1最后加起来(即对应位置的激活值相加)便可得到第二列的结果。蓝色部分的激活值大于红色部分。
- 第三列为fm1中最大激活值映射回input的结果(黑色方框为本例的可视化结果,其余三个为类似图像的可视化结果),以第一张图像为例,可以看到最大激活值对应的可视化结果是狗的面部特征(刚好对应第一行第二列fm1中的蓝色区域)。
- 第四列的结果是怎么得到的:类似于第二列结果得到的方式,也是将灰色块从图像的左上角一直遍历滑动到右下角,以灰色块滑动的第一个位置为例(假设滑动从左上角开始),如果这张左上角被遮挡的图像被分类器预测为“博美犬”,那么该灰色块覆盖的区域我们就记为“博美犬”(即该区域内每个像素点被标记为“博美犬”这个类别),剩余的位置以此类推,最终统计input图像中每个像素点被分类正确的概率。以第一张图像为例,当灰色块遮挡住狗的面部时,类别“博美犬”的概率会大幅下降。
- 第五列是第四列结果的延伸,为input图像每个像素点对应的概率最高的类别。对于第一张图像,大部分位置的预测结果都是“博美犬”(如果使用灰色块遮挡狗的面部但不遮挡球,则预测结果会变为“网球”)。对于第二张图像,虽然Layer5最大激活值的可视化结果是车身上的文字,但是分类器却对车轮更为敏感。对于第三张图像,其包含多个目标(两个人和一只狗),虽然Layer5最大激活值的可视化结果是人脸,但是分类器却对狗更为敏感。
因此,对于本节一开始提出的问题,ZFNet作者得出的结论是:模型在进行图像分类任务时,确实识别出了目标的位置。
4.3.对应分析(Correspondence Analysis)
深度学习模型不同于许多现有的识别方法,因为其没有明确的机制来建立不同图像中特定对象之间的对应关系(例如,面部眼睛或者鼻子所具有的特殊空间结构)。但是,一个深度学习模型可能会隐式的计算这些关系。ZFNet作者也对此进行了研究:
直白的说,举个例子:Correspondence Analysis就是在研究不同品种的狗之间的左眼是否具有某些共性的特征。而ZFNet的作者也想知道神经网络是否隐式的学到了这些共性特征。

在Fig8中,作者随机挑选了5张狗的正面照(第1列),对于第2列~第4列,分别遮挡其右眼、左眼、鼻子。剩余的列则随机进行遮挡。
对于每张图像$i$,计算:
\[\epsilon_i^l = x_i^l - \tilde{x}_i^l\]其中,$x_i^l, \tilde{x}_i^l$分别为未遮挡图像(即原始图像)和遮挡图像在层$l$的特征向量。使用以下方式测量层$l$中所有不同图像对$(i,j)$(即每一列的任意两幅图像)之间的一致性:
\[\Delta _l = \sum^5_{i,j=1,i\neq j} \mathcal{H}(sign(\epsilon_i^l), sign(\epsilon_j^l))\]其中,$\mathcal{H}$为海明距离。$\Delta _l$值越小,一致性越好。
sign为符号函数:
- 当$x>0,sign(x)=1$
- 当$x=0,sign(x)=0$
- 当$x<0,sign(x)=-1$
Layer5和Layer7的一致性结果见下:
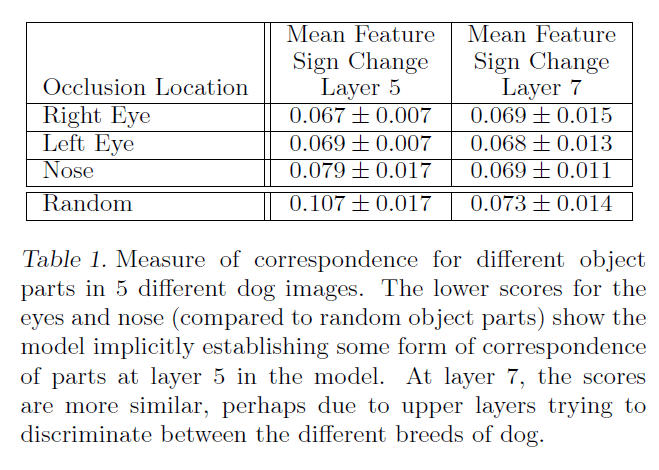
Layer5的眼睛和鼻子的一致性明显好于随机,因此可以说明神经网络确实隐式的计算了共性特征。
Layer7中眼睛、鼻子和随机的一致性差别不大,可能是因为浅层(例如Layer5)着重在识别一类物品或物体所具有的共性特征(例如狗的鼻子和眼睛),而深层(例如Layer7)则主要在识别一些更复杂和宏观的特征(例如狗的品种等)。
从Fig2中也能看到,Layer5确实学到的都是狗的一些面部特征,和这里的结论吻合。
5.实验(Experiments)
5.1.ImageNet 2012
ImageNet2012包含1.3M训练集,50k验证集,100k测试集,共有1000多个类别。ZFNet在该数据集的表现见下:
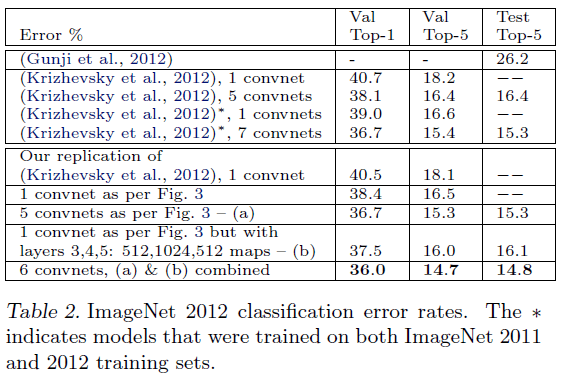
5 convnets指的是使用5个该卷积网络进行预测,结果取平均。
表2中倒数第二行中的模型(b)是在ZFNet的基础上,将Layer3,4,5的卷积核数量分别改为512,1024,512。表中最后一行是将模型(a)和模型(b)综合起来得到的预测结果。
作者在ImageNet2012验证集上复现了AlexNet(1 convnet)的结果,误差在1%(18.1% vs. 18.2%)。ZFNet最终得到了14.8%的Top5测试集错误率,低于AlexNet的15.3%。
此外,作者还拿ZFNet和非卷积网络模型(表2第一行)进行了比较,发现ZFNet的错误率只有非卷积网络模型的一半。
不同的ImageNet模型尺寸(Varying ImageNet Model Sizes):

作者尝试去掉不同的层或修改FC层的size,测试结果见Table3。
5.2.特征泛化(Feature Generalization)
为了测试该模型在其他数据集上的表现,作者使用了两种不同的训练方法:1)固定Layer1~Layer7的结构和参数,只是使用新的数据集重新训练了softmax层;2)使用新的数据集重新训练整个模型。
Caltech-101数据集测试结果:
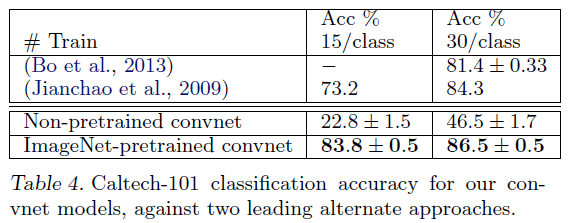
作者从Caltech-101数据集的每个类别中分别选取15张或者30张图像作为训练集,测试集中每个类别最多选取50张图像。使用5折交叉验证。结果见Table4,可以看出,使用预训练的ZFNet模型准确率明显高于重新训练的ZFNet模型,说明数据集的大小对模型的性能影响至关重要。此外,预训练的ZFNet模型准确率高于未使用卷积网络的传统优秀算法。
Caltech-256数据集测试结果:
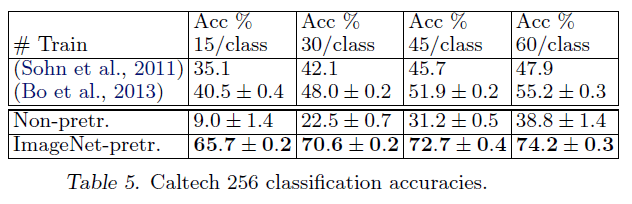
这次每个类别分别选择15,30,45,60张图像作为训练集。
准确率随着每个类别图像张数的变化趋势:

从Fig9中可以看出,ZFNet使用更少的数据便可以获得比传统优秀算法更高的准确率。
PASCAL2012数据集测试结果:
测试使用了标准的训练集和验证集,一共20个类别,测试结果见下:
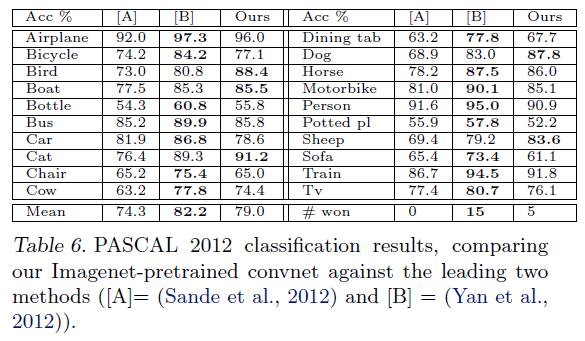
因为PASCAL2012数据集和ImageNet数据集差异较大,因此预训练的ZFNet模型表现一般。
5.3.特征分析(Feature Analysis)
ZFNet作者探讨了ImageNet预训练模型的每一层是如何区别特征的。结果如下表所示:

第一列括号中的数字代表重新训练的层数。输出层分别使用了线性SVM和softmax。上述结果说明了更深的层识别特征的能力更强。
6.讨论(Discussion)
本文提出了一种创新的可视化卷积神经网络的方法,并且可以通过可视化的结果来优化网络参数。此外,ZFNet可以很好的泛化到其他相似数据集(例如Caltech-101和Caltech-256)。
7.原文链接
👽Visualizing and Understanding Convolutional Networks
