本文为原创文章,未经本人允许,禁止转载。转载请注明出处。
1.Introduction
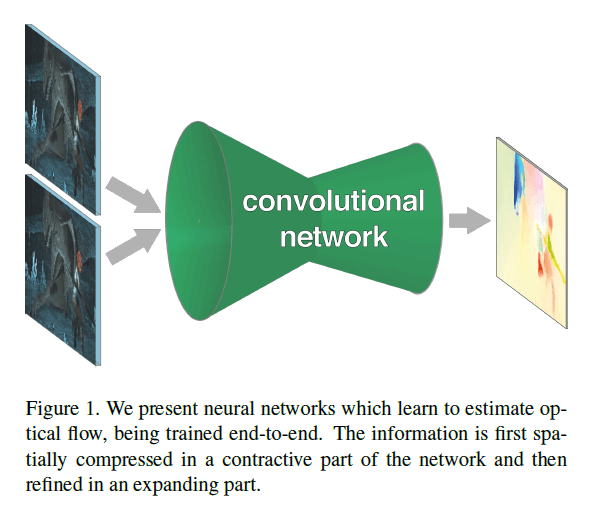
CNN在CV的许多领域得到了广泛的应用。其被应用于图像分类、语义分割、基于单张图像的深度估计等。在本文中,我们训练了一个端到端的CNN网络,以从一对图像中预测出光流场。
光流估计即需要精确定位每个像素,同时也需要找到两张输入图像之间的对应关系。这不仅涉及对图像表征的学习,还涉及学习在两幅图像中的不同位置去匹配这些特征。在这方面,光流估计和之前的那些基于CNN的应用有着本质的不同。
由于尚不清楚这项任务是否可以用标准的CNN框架来完成,我们还开发了一个带有相关层(correlation layer)的框架,其可以明确提供匹配能力。该框架的训练是端到端的。想法是利用CNN在多尺度和多抽象级别上学习强特征的能力,以帮助寻找基于这些特征的实际对应关系。相关层后续的层用于学习从这些匹配中预测流。令人惊讶的是,即使不使用相关层,原始的网络也能得到具有竞争力的准确率。
训练这样的网络通常需要一个很大的训练集。尽管有数据扩展的帮助,但现有的光流数据集仍然太小,无法训练出一个SOTA的网络。众所周知,从真实视频中获取光流的GT是非常困难的。因此我们以真实换取数量,我们合成了一个飞行椅子的数据集,前景是椅子,背景是各种各样的随机背景图像。仅在这样一个合成的数据集上训练的CNN模型,即使不进行fine-tune,也能很好的推广到真实数据集。
利用CNN在GPU上的高效实现,我们的方法比大多数竞争对手都快。在Sintel数据集的全分辨率下,我们的网络每秒可以预测多达10个图像对的光流,在实时方法中精度是最高的。
2.Related Work
👉Optical Flow.
自”B. K. P. Horn and B. G. Schunck. Determining optical flow. Artificial Intelligence, 17:185–203, 1981.”以来,变分方法(variational approaches)一直主导着光流估计。后续很多研究都对其进行了改进。我们只是用变分方法对CNN预测的光流场进行可选的refinement,而不需要任何手工设计的聚合、匹配和插值方法。
也有一些研究将机器学习技术应用于光流估计。
目前已经有一些无监督学习的工作,使用神经网络模型对视频帧之间的位移(disparity)进行学习。但在真实视频上,其没有明显好于传统算法。
3.Network Architectures
👉Convolutional Networks.
CNN在大规模图像分类方面表现良好。这为CNN在CV领域中各项任务上的应用奠定了基础。
虽然目前还没有将CNN用于光流估计的相关工作,但是已经有从CNN进行匹配的一些研究。”P. Fischer, A. Dosovitskiy, and T. Brox. Descriptor matching with convolutional neural networks: a comparison to SIFT. 2014. pre-print, arXiv:1405.5769v1 [cs.CV].”从以有监督或无监督方式训练的CNN网络中提取表征,并基于欧氏距离匹配这些特征。”J. Zbontar and Y. LeCun. Computing the stereo matching cost with a convolutional neural network. CoRR, abs/1409.4326, 2014.”训练具有Siamese框架的CNN来预测图像patch之间的相似性。这些方法与我们方法的一个显著区别是,它们是基于patch的,并将空间聚合留给后处理,而本文中的网络则直接预测完整的光流场。
最近CNN的应用包括语义分割、深度预测、关键点检测和边缘检测等。这些任务类似于光流估计,因为它们都涉及对每个像素进行预测。因为我们的模型框架在很大程度上受到了这些针对每个像素都进行预测的任务的启发,我们简要回顾了一些不同的方法。
最简单的方法是以滑动窗口的方式应用传统CNN,从而为每个图像patch计算一个预测结果(比如类标签)。这一方法在很多情况下都能很好的工作,但其也有缺点:一是计算成本高;二是针对patch进行计算,没有考虑全局特性。另一个简单的方法是将所有的feature map都上采样至想要的全分辨率,并将它们堆叠在一起,从而产生对每个像素的预测。
Eigen等人(D. Eigen, C. Puhrsch, and R. Fergus. Depth map prediction from a single image using a multi-scale deep network. NIPS, 2014.)通过训练一个输入为coarse prediction和输入图像的额外网络来对coarse depth map进行refine。Long等人和Dosovitskiy等人(A. Dosovitskiy, J. T. Springenberg, and T. Brox. Learning to generate chairs with convolutional neural networks. In CVPR, 2015.)使用上卷积层(upconvolutional layers,通常也被称为deconvolutional layers,尽管其在操作技术上仍是卷积,而不是反卷积)来对coarse feature maps进行迭代refine。我们的方法综合了以上工作的思想。与Long等人的工作不同,我们不仅反卷积了coarse prediction,还对整个coarse feature maps进行了反卷积,从而将更high-level的信息传递给fine prediction。与Dosovitskiy等人的工作不同,我们将反卷积的结果和网络收缩部分(‘contractive’ part)的特征concat在一起。
众所周知,在给定足够多的标注数据的情况下,CNN非常擅长学习输入-输出之间的关系。因此,我们采用端到端的方式来预测光流:输入为图像对和真实的光流(GT),输出为预测的x-y光流场。
一个简单的解决办法是把两个输入图像直接堆叠在一起喂给一个通用的网络,让网络自己学习如何处理图像对并从中提取运动信息。见Fig2上。我们将这个只包含卷积层的框架称为FlowNetSimple。
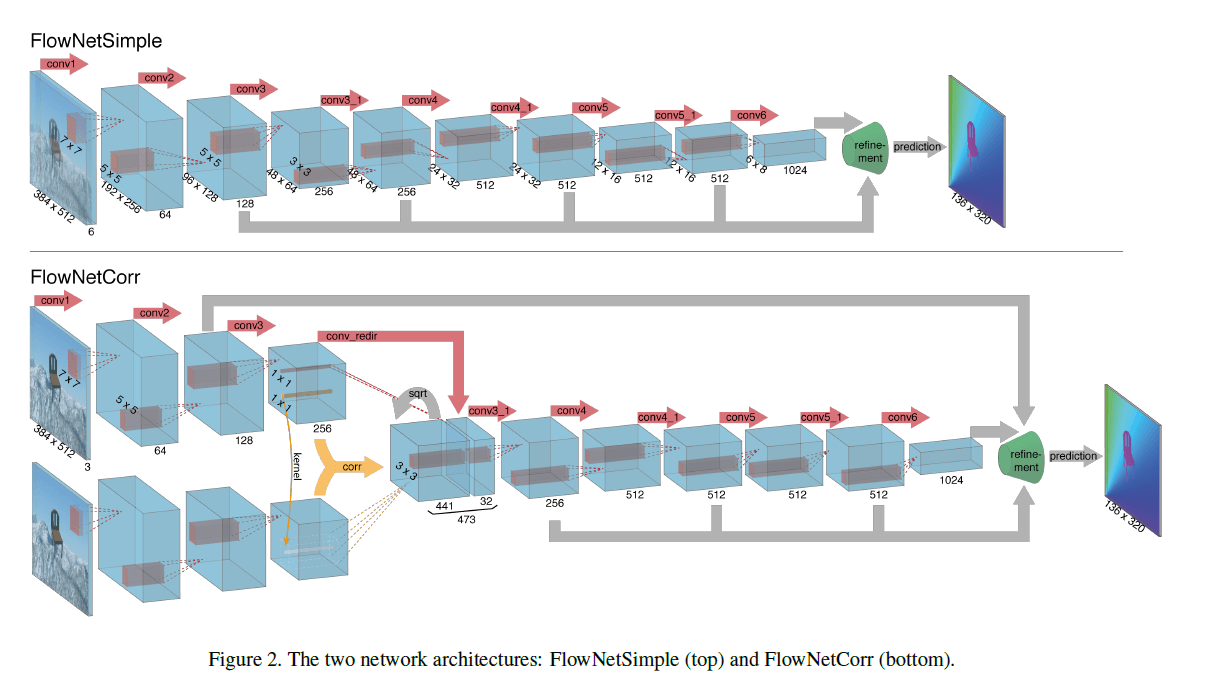
原则上,只要这个网络足够大,其就能学会预测光流。然而,我们永远不能确定像随机梯度下降法这样的局部梯度优化是否能让网络达到这一点。因此,手工设计一种不太通用的框架可能是有益的,在给定数据和优化技术下可能会表现的更好。
一个简单的步骤是为这两张图像创建两个独立但相同的处理流,并在后面的阶段将其组合,见Fig2下。在这个框架中,网络先分别为两张图像生成有意义的表征,并在higher level上组合它们。这类似于标准匹配方法,即先分别从两张图像的patch中提取特征,然后再比较这些特征向量。然而,给定两幅图像的表征,网络该如何找到对应关系?
为了帮助网络进行匹配,我们引入了相关层,用于在两个feature map之间进行比较。我们将包含相关层的框架称为FlowNetCorr,见Fig2下。给定两个多通道feature map $\mathbf{f}_1,\mathbf{f}_2 : \mathbb{R}^2 \to \mathbb{R}^c$,并且$w,h,c$分别表示宽、高和通道数,相关层会将$\mathbf{f}_1$中的每个patch与$\mathbf{f}_2$中的每一个patch进行比较。
首先,我们先只考虑两个patch之间的比较。第一个map的patch的中心点为$\mathbf{x}_1$,第二个map的patch的中心点为$\mathbf{x}_2$,其之间的相关性(correlation)定义为:
\[c(\mathbf{x}_1,\mathbf{x}_2) = \sum_{\mathbf{o} \in [-k,k]\times [-k,k]} \langle \mathbf{f}_1 (\mathbf{x}_1 + \mathbf{o}), \mathbf{f}_2(\mathbf{x}_2 + \mathbf{o}) \rangle \tag{1}\]其中方形patch的大小为$K:=2k+1$。式(1)的计算方式类似于卷积,但不是数据和卷积核进行卷积,而是数据和数据进行卷积。所以其没有可训练的权重参数。
$c(\mathbf{x}_1,\mathbf{x}_2)$的计算包含$c \cdot K^2$次乘法运算(个人理解:$c$是feature map的通道数,在每个通道上,两个大小为$K$的patch之间进行逐元素的比较,这里比较用的是乘法运算,那么就是$K^2$次乘法,所以如果考虑所有通道,那么乘法运算的总次数为$c \cdot K^2$)。$\mathbf{f}_1$中的一个patch需要和$\mathbf{f}_2$中的所有patch进行比较,那就是$c \cdot K^2 \cdot w \cdot h$次乘法,如果考虑$\mathbf{f}_1$中的所有patch,那么就需要$c \cdot K^2 \cdot w^2 \cdot h^2$次乘法,巨大的计算量使得模型训练和推理变得困难。因此,由于计算量的原因,我们限制了比较的最大位移,并在两个feature map中引入了跨步。
个人理解:将两个patch的相关性作为这两个patch中心点的相关性。
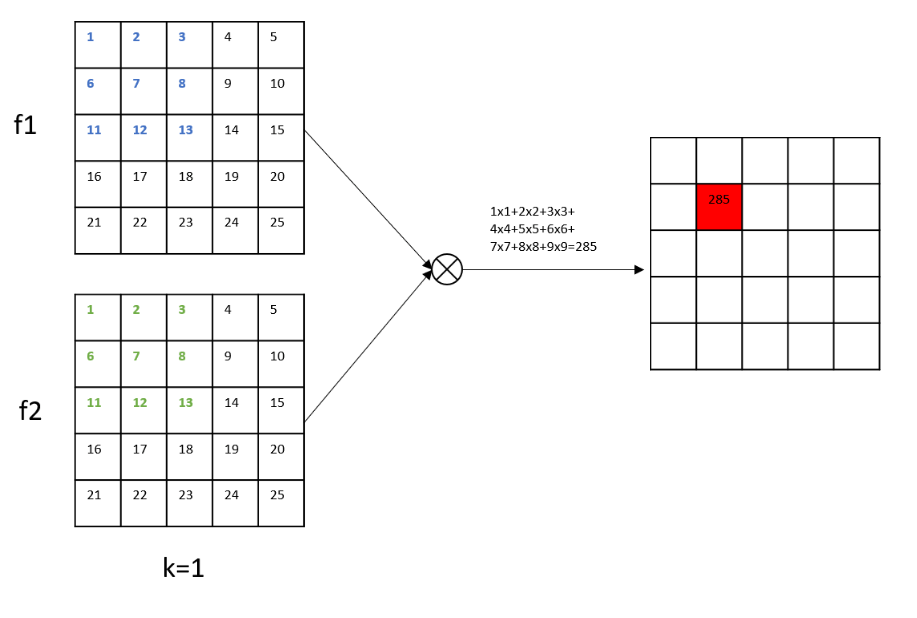
上图是一个例子,$\mathbf{f}_1$中的25个元素会依次和$\mathbf{f}_2$中的25个元素以基于patch($3\times 3$大小)的形式计算相关性。
因为这样做计算量太大,我们不想让$\mathbf{f}_1$中的25个元素依次和$\mathbf{f}_2$中的25个元素进行计算,因此,我们限制只和$\mathbf{f}_2$中的部分元素进行计算,这些元素都在$\mathbf{f}_1$目标元素的附近。我们假设这个范围为$D:=2d+1$。
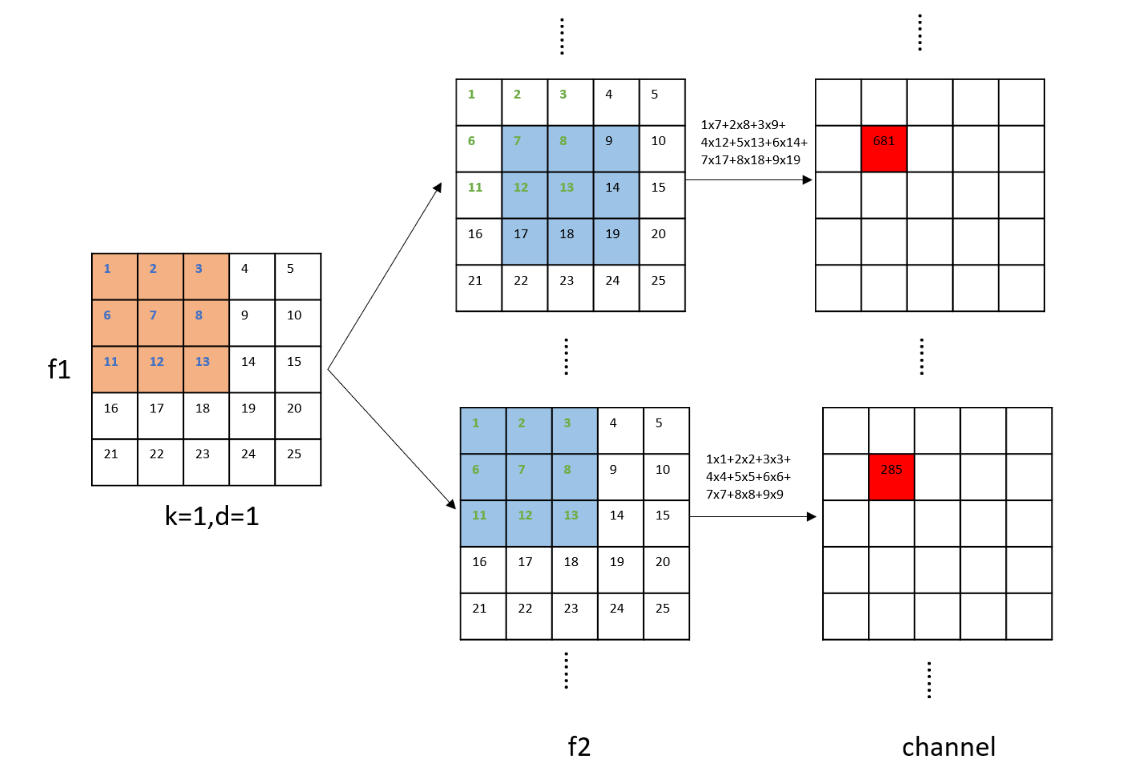
举个例子,假设我们要计算$\mathbf{f}_1$中$(1,1)$(数值为7)这个元素的相关性,那么我们只考虑$\mathbf{f}_2$中$(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)$这9个元素(即$d=1$,一共计算$D^2$次)。依旧是基于patch进行计算(这个patch的大小由k控制)。$\mathbf{f}_1$中同一个元素和$\mathbf{f}_2$中不同元素的相关性按channel方向排列,因此通过相关层后得到的feature map大小应该是$D^2 \times w \times h$,其中$w,h$为feature map的宽和高,$D^2$为channel数量。此外,对于$\mathbf{x}_1$和$\mathbf{x}_2$,我们还分别使用了$s_1$和$s_2$的步长。
作者使用k=0,即K=1,这样就不用考虑padding操作了,并且计算量也小了很多。
$D^2$太大时,作者使用了stride操作来降低通道数量。在FlowNetCorr中,作者取d=20,那么D就是41,输出的feature map大小理应是$1681 \times h \times w$,但这样维度就太大了,因此作者使用了stride操作,使$D=21$,将维度降为$441 \times h \times w$。这个可以从Fig2中可以看到。
此外,FlowNetCorr中还有一个
conv_redir,这个就是卷积层+BatchNorm+LeakyReLU这一套操作。
👉Refinement.
CNN擅长通过卷积层和池化层来提取图像high-level的抽象特征。池化操作使得训练网络变得可行,其可以在输入图像的大范围区域内聚合信息。然而,池化会导致分辨率降低,因此为了得到基于每个像素的dense prediction,我们需要refine这些经过池化的粗糙表征信息。

refinement的流程见Fig3。主要结构就是反卷积层,其由unpooling和卷积组成。反卷积层在之前的研究中都有使用,比如ZFNet、GAN、FCN等。为了执行refinement,我们将反卷积应用于feature map,并将其与网络“收缩”阶段对应大小的feature map concat在一起,并且会对得到的粗糙光流预测结果进行上采样(如果需要的话),并且会将上采样得到的粗糙预测结果也concat在一起。通过这种方式,我们既保留了从粗糙feature map来的high-level的信息,也保留了在网络浅层的feature map提供的较精细的局部信息。每一步会增加两次分辨率。我们重复了4次该操作,得到的预测光流场的分辨率仍然比输入分辨率小了4倍。相比使用计算成本较低的双线性上采样将其恢复至原始输入分辨率,进一步对该分辨率进行refinement并不能显著改善结果。因此,我们使用双线性上采样来得到最终预测的光流场。
还有另一种方案是使用“T. Brox and J. Malik. Large displacement optical flow: descriptor matching in variational motion estimation. PAMI, 33(3):500–513, 2011.”一文中提供的变分方法来代替双线性上采样,作者使用光流的亮度约束和平滑约束构建了一个能量函数,然后通过迭代的方法来最小化能量函数,从粗糙到精细一共迭代了20次,从而得到原始分辨率的光流预测结果。并且我们在原始分辨率上多运行了5次迭代。此外,我们还使用论文“M. Leordeanu, R. Sukthankar, and C. Sminchisescu. Efficient closed-form solution to generalized boundary detection. In Proceedings of the 12th European Conference on Computer Vision - Volume Part IV, ECCV’12, pages 516–529, Berlin, Heidelberg, 2012. Springer-Verlag.”中的方法来计算图像边界,并使用$\alpha = \text{exp} (-\lambda b(x,y)^{\kappa})$替换平滑项系数以重视检测到的边界。相比简单的双线性上采样,这种方法计算成本更高,但也引入了变分的优点,得到的光流结果更为平滑和准确。在下文中,我们使用后缀“+v”来表示这种方法。方法之间的比较见Fig4。

从Fig4可以看出,变分方法的使用加强了对小运动的检测能力(Fig4第一行)。而对于较大的运动(Fig4第二行),变分方法并不能校正较大的误差,但是可以平滑光流场,从而降低EPE。
4.Training Data
对于光流估计任务来说,GT的获得是很困难的,因为很难确定像素之间的对应关系。目前可获得的数据集见表1。
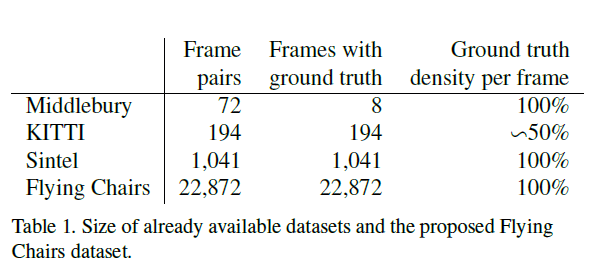
4.1.Existing Datasets
Middlebury数据集只有8个图像对有GT,可以用于训练。数据集的位移很小,基本在10个像素以内。
KITTI数据集会更大一些,有194个带标注的图像对可以用于训练,并且有大位移,但是该数据集只包含一种非常特殊的运动类型。该数据集通过相机和3D激光扫描仪同时记录场景,来获得真实世界场景的GT。但其无法捕捉到遥远物体(如天空)的运动,从而导致GT是稀疏的。
MPI Sintel数据集从人工渲染的场景中获得GT。数据集提供了两个版本:Final版本包含运动模糊和大气效果(如雾);Clean版本则不包含这些效果。Sintel数据集是目前可用的最大数据集(每个版本都有1041个带有标注的图像对可用于训练),并且GT是dense的。
4.2.Flying Chairs
Sintel数据集对于训练CNN来说还是太小了。为了得到充足的训练数据,我们使用一组公开的3D椅子模型,通过仿射变换,合成了一个飞椅数据集。首先,我们从Flickr中检索了964张分辨率为$1024 \times 768$的图片,分为以下几类:“city”(321张)、“landscape”(129张)、“mountain”(514张)。我们将图像切成4块,使用得到的$512 \times 384$大小的图像作为背景。我们将椅子作为前景添加进去。从原始数据集中,我们删掉了非常相似的椅子,得到了809种椅子类型和每把椅子的62个视图。一些例子见Fig5。

Fig5中前三列是正常的图像,后三列是数据扩展得到的图像。
为了生成运动,我们对背景和椅子进行了随机的仿射变换。
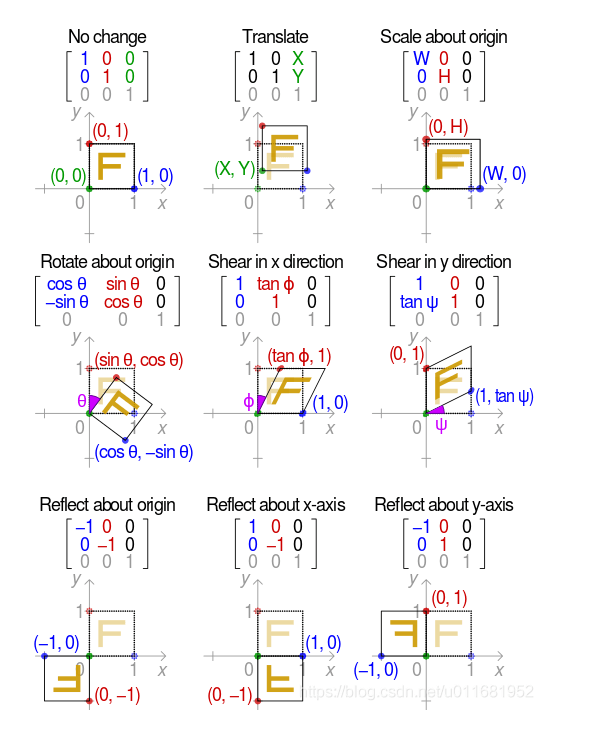
仿射变换(Affine Transformation)是线性变换和平移变换的叠加。仿射变换包括缩放(scale)、平移(transform)、旋转(rotate)、反射(reflection)、错切(shear mapping)。
仿射变换过程中一些性质保持不变:
- 凸性。
- 共线性:若几个点变换前在一条线上,则仿射变换后仍然在一条线上。
- 平行性:若两条线变换前平行,则变换后仍然平行。
- 共线比例不变性:变换前一条线上两条线段的比例,在变换后比例不变。
在二维图像中,仿射变换一般表示为:
\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} R_{00} & R_{01} & T_x \\ R_{10} & R_{11} & T_y \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix}\]可视为线性变换R和平移变换T的叠加。
使用计算机图形学技术,将生成的椅子以透视投影的方式渲染到背景图像上,形成合成图像。在渲染过程中,还会考虑光照、阴影等因素,使得合成图像看起来更加真实。通过合成图像的前一帧和当前帧之间的像素位移,计算出对应的光流场。光流场表示了像素在两个帧之间的运动情况。
每个图像对的参数都是随机的,这些参数包括:1)椅子的数量、类型、尺寸和初始位置;2)仿射变换参数。我们随机调整这些参数的分布,以使得到的位移直方图和Sintel数据集的位移直方图相似(细节见补充材料)。通过这一方法,我们生成了一个包含22872个图像对及其对应光流场的数据集(每张背景图像会被使用多次)。这个数据集的大小是任意选择的,原则上可以更大。
4.3.Data Augmentation
用于增强网络泛化性的一个常用策略就是data augmentation。尽管飞椅数据集已经相当大了,我们仍然发现data augmentation可以有效防止过拟合。我们使用的data augmentation方法有:几何形变(平移、旋转、缩放)、高斯噪声、亮度,对比度,gamma以及颜色的改变。所有这些操作都在GPU上进行。一些augmentation的例子见Fig5。
我们不但想增加图像的种类,还想增加光流场的种类。因此,假设有图像对A和B,我们对A和B施加相同的强几何变换,然后保持A不变,对B施加较小的变换,从而得到一个光流场;反过来,保持B不变,对A施加较小的变换,又能得到一个光流场。
我们平移的范围是$[-20\%,20\%]$,旋转范围是$[-17°,17°]$,缩放范围为$[0.9,2.0]$。高斯噪声的sigma在$[0,0.04]$范围内均匀取值。对比度取值范围为$[-0.8,0.4]$。RGB每个通道的相乘系数取值范围为$[0.5,2]$。gamma的取值范围为$[0.7,1.5]$。使用sigma为0.2的高斯函数进行亮度的改变。
5.Experiments
我们在Sintel、KITTI、Middlebury和飞椅数据集上汇报了我们网络的结果。我们还实验了在Sintel数据上进行fine-tune,并使用了变分refinement。此外,我们还比较了我们的网络和其他方法的runtime。
5.1.Network and Training Details
我们训练所用的网络框架见Fig2。总的来说,我们尽量保持不同网络的框架一致:在Fig2中,两种网络都有9个卷积层,其中有6个卷积层的步长为2(最简单的pooling方式),每一层后面都跟了一个ReLU函数。我们没有使用全连接层,因此输入可以是任意大小的。卷积核的大小随着网络的深入而减小:第一层卷积核大小为$7 \times 7$,接下来两层的卷积核大小为$5 \times 5$,从第四层开始卷积核大小为$3 \times 3$。feature map基本上在每次下采样后通道数翻倍。针对FlowNetC中的相关层,我们设$k=0,d=20,s_1=1,s_2=2$。我们使用EPE(endpoint error)作为training loss,这是光流估计的标准误差度量。EPE就是估计的光流向量与真实光流向量之间的欧氏距离,所有像素点的误差会做一个平均。
使用caffe训练网络。使用Adam优化器,因为在我们的任务上,它比momentum收敛的更快。Adam优化器的参数设置为$\beta_1 = 0.9, \beta_2 = 0.999$。从某种意义上来说,由于每个像素都是一个训练样本,因此我们使用了相当小的batch size,每个batch只有8个图像对。前300k次迭代的学习率为$\lambda = 1e-4$,之后每100k次迭代,学习率缩小2倍。对于FlowNetCorr,我们发现$\lambda = 1e-4$的学习率会导致梯度爆炸。为了解决这个问题,我们刚开始使用一个很低的学习率$\lambda = 1e-6$,在10k次迭代后,学习率缓慢上升至$\lambda = 1e-4$,然后再遵循之前提到的学习率衰减策略。
为了防止在训练和fine-tune时出现过拟合,我们将飞椅数据集分为22232个训练样例和640个测试样例,将Sintel中的908个图像对用于训练,133个图像对用于验证。
我们发现在推理阶段放大输入图像可以提高性能。尽管放大的倍数取决于数据集,但我们不管什么任务,只是为每个网络固定了一个放大倍数。对于FlowNetS,我们没有使用放大,对于FlowNetC,我们使用的放大倍数为1.25。
👉Fine-tuning.
使用的数据集在目标类型和运动方式上都各有不同。一个标准的解决方案是在目标数据集上进行fine-tune。KITTI数据集比较小,且只有稀疏的标注。因此我们在Sintel训练集上进行fine-tune。我们使用的图像来自Sintel的Clean和Final版本,使用较低的学习率$\lambda = 1e-6$ fine-tune了几千次迭代。为了获得最佳性能,我们先使用验证集确定最佳迭代次数,然后在训练集上fine-tune相同的迭代次数。我们用后缀”+ft”表示fine-tune过的网络。
5.2.Results
在表2中,我们展示了我们的方法和其他一些表现优秀的方法在公开数据集(Sintel、KITTI、Middlebury)和飞椅数据集上的EPE。此外,我们还展示了不同方法在Sintel上的runtime。
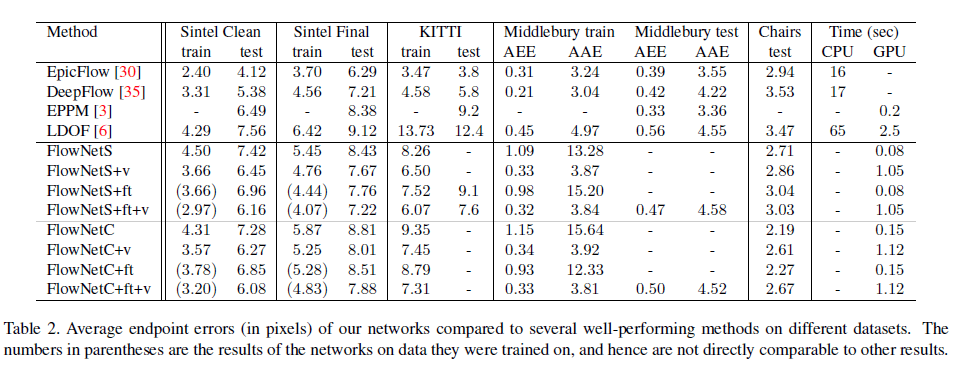
表2中带括号的数据指的是这些网络在其训练数据上的测试结果,因此无法与其他结果直接比较。
仅在飞椅这样一个非真实数据集上训练得到的网络,在真实光流数据集上表现非常好,比如击败了著名的LDOF算法。在Sintel Final和KITTI数据集上,经过在Sintel上fine-tune过的FlowNet的表现优于同为实时检测的EPPM,并且速度是EPPM的两倍。
👉Sintel.
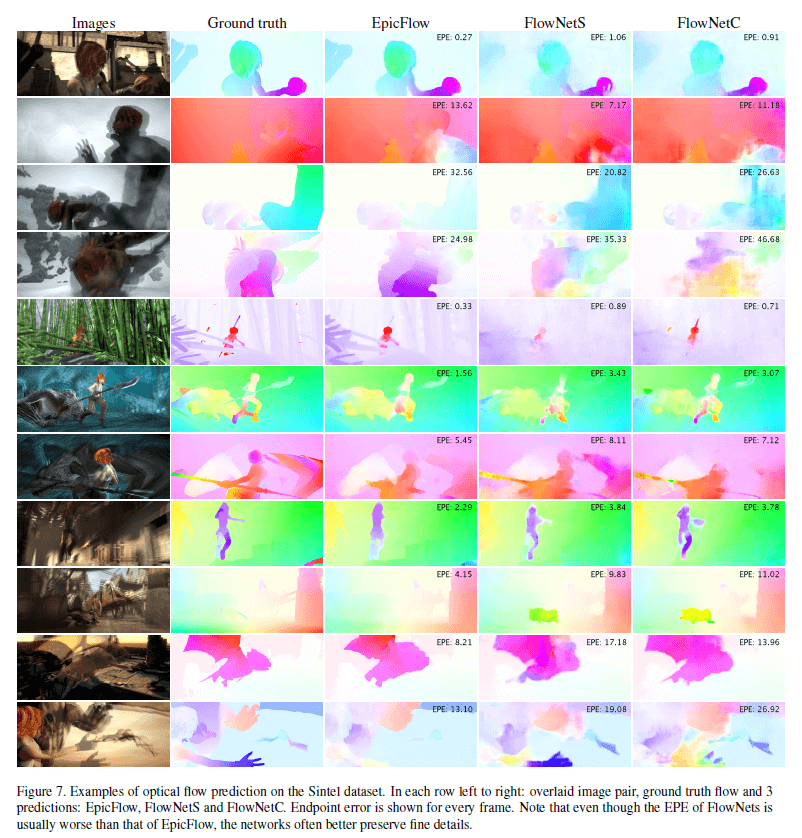
从表2中可以看出,在Sintel Clean数据集上,FlowNetC优于FlowNetS,但是在Sintel Final数据集上,情况却刚好相反。在一些困难数据集上,FlowNetS+ft+v的表现和DeepFlow不相上下。由于EPE更倾向于过度平滑的方法,因此我们还进行了定性分析。Fig7展示了我们的方法(无fine-tune)和EpicFlow的比较。在Fig7中,我们的方法虽然EPE更高,但是在视觉上,我们的结果是更好的。其中一个原因就是我们的输出不平滑。这一点我们可以通过对变分的改进(见第3部分Refinement)来进一步优化。
👉KITTI.
KITTI包含强投影变换(strong projective transformations),这和飞椅数据集中用到的变换非常不同。但即使这样,仅在飞椅数据集上训练得到的网络的效果依然相当的不错,再加上fine-tune和variational refinement(见第3部分Refinement),网络性能得到进一步的提升。有趣的是,在Sintel上进行fine-tune之后提升了其在KITTI数据集上的表现,这可能是因为相比飞椅数据集,Sintel数据集的图像和运动更为自然。在KITTI数据集上,FlowNetS的表现优于FlowNetC。
👉Flying Chairs.
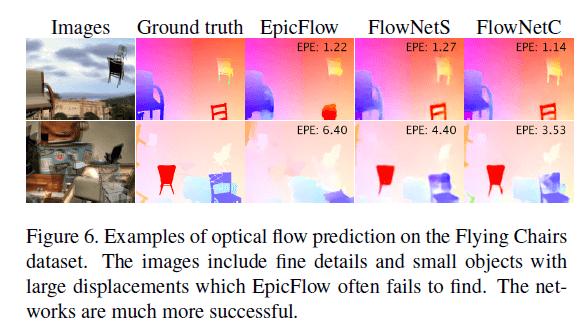
我们的网络是在飞椅数据集上训练的,因此其理应在该数据集上表现最好。我们留出640张图像用于测试。不同方法在飞椅数据集上的预测结果见Fig6。从Fig6中可以看出,FlowNetC是表现最好的。并且还有一个有趣的发现:只有在这个数据集上,variational refinement不能提升性能,反而使其变得更糟糕。
👉Timings.
在表2中,我们展示了不同方法处理一帧需要的秒数。不幸的是,许多方法只提供了在单个CPU上的runtime,而我们的方法只提供了在GPU上的runtime。虽然我们的方法在准确率方面可能不如一些之前的SOTA方法,但是我们的方法在具有实时性的方法中是最好的。训练和推理我们都使用了NVIDIA GTX Titan GPU。DeepFlow和EpicFlow在CPU上的运行时间数据来自论文“J. Revaud, P. Weinzaepfel, Z. Harchaoui, and C. Schmid. EpicFlow: Edge-Preserving Interpolation of Correspondences for Optical Flow. In CVPR, Boston, United States, June 2015.”,LDOF的runtime在单个2.66GHz core上测得。
5.3.Analysis
👉Training data.
为了验证我们的方法是从飞椅数据集获益而不是Sintel数据集,我们仅在Sintel数据集上也训练了一个网络,并且预留了一个验证集用于控制性能。得益于有效的data augmentation,即使只有一个Sintel数据集也足以很好的学习光流。相比在飞椅数据集上训练并在Sintel上fine-tune的模型,只在Sintel上训练的模型在Sintel数据集上的EPE要高出1个像素左右。
飞椅数据集已经相当大了,那么data augmentation还是必须的吗?答案是必须的:在飞椅数据集上训练,如果不使用data augmentation,在Sintel上测试得到的EPE会升高2个像素左右。
👉Comparing the architectures.
FlowNetS和FlowNetC的比较结果见表2。
首先,FlowNetS在Sintel Final上的结果好于FlowNetC。但在飞椅数据集和Sintel Clean上,FlowNetC优于FlowNetS。和Sintel Final数据集不同,飞椅数据集不包含运动模糊或者雾。这些结果共同表明,尽管两个模型的参数量几乎相同,但FlowNetC更容易对训练数据产生过拟合。虽然目前来看这是一个弱点,但如果有更好的训练数据,这也可能会成为一个优势。
其次,FlowNetC看起来不擅长处理大位移。从其在KITTI数据集上的表现可以看出这一点,相同的结论也可以从Sintel Final数据集中获得。在位移至少为40个像素(s40+)的数据上,FlowNetS+ft的EPE为43.3个像素,FlowNetC+ft的EPE为48个像素。一个解释就是相关性计算时设置的各种范围限制了其对大位移的预测能力。如果增大范围(计算成本也会相应增加),对大位移的预测能力也会有所提升。
6.Conclusion
我们证明了使用CNN从两个输入图像中直接预测光流是可行的。并且训练数据不需要是真实的。在飞椅数据集训练得到的模型足以预测自然场景中的光流,并取得不错的效果。这证明了我们所提出的网络的泛化能力。在飞椅测试集上,我们的方法甚至优于SOTA的DeepFlow和EpicFlow。
7.Supplementary Material
7.1.Flow field color coding
为了可视化光流场,我们使用了Sintel提供的工具。使用彩色像素值来表示流的方向和大小。白色表示没有运动。光流的颜色编码见Fig1:将某一像素点的光流向量的起点移至Fig1方块的中心位置,即可得到该光流向量的颜色编码。因为不同图像对的光流大小差异很大,所以我们独立的对每个图像对的最大颜色强度都进行了归一化,但在同一个图像对上的不同方法采用相同的方式。

7.2.Details of generating Flying Chairs
接下来我们详细解释下飞椅数据集的生成过程。背景是来自Flickr的964张分辨率为$1024 \times 768$的图像。前景我们使用了809个椅子模型,共有62个视图:31个方位角(azimuth angle)和2个仰角(elevation angle)。我们选取一个背景,然后随机放置一组椅子,作为图像对中的第一张图像。椅子的数量在[16;24]之间均匀取样,对椅子的类型、视图和位置也进行均匀采样。椅子的大小(即像素个数)使用均值为200,标准差也为200的高斯采样,区间控制在50到640之间。
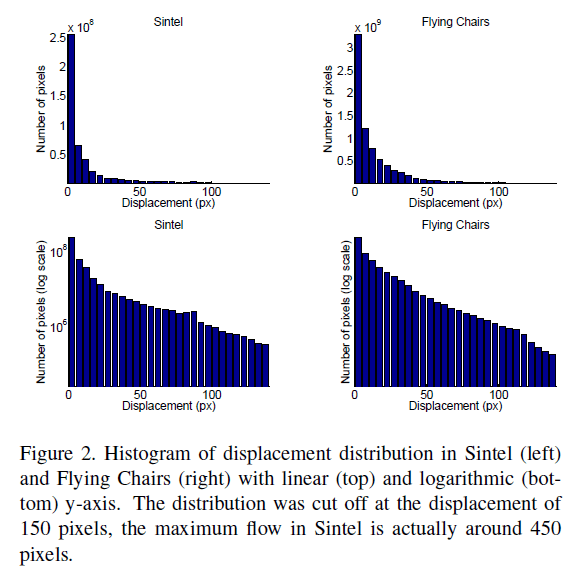
为了生成图像对中的第二张图像和光流场,我们对椅子和背景施加随机的变换。每一种变换都是缩放、旋转和平移的组合。我们需要采样的是缩放系数、旋转角度和平移矢量。我们的目标是大致匹配Sintel数据集的位移分布,见Fig2左。简单的按照高斯分布对变换参数进行采样会导致太少的小位移,因此我们使变换参数的分布更多的集中在0附近。
实际我们采样所用的分布是两个分布的混合。采样所用的分布见下:
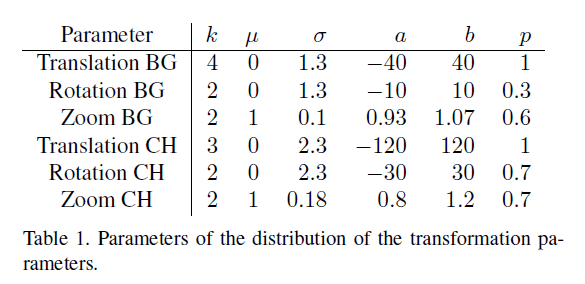
\[\xi = \beta \cdot \max(\min(\text{sign}(\gamma) \cdot \lvert \gamma \rvert ^k,b),a) + (1-\beta) \cdot \mu\]其中,$\gamma \sim \mathcal{N}(\mu,\sigma)$是单变量高斯分布,$\beta$是伯努利随机变量(表1中$p$就是$\beta$的取值)。剩余参数的取值见表1。
给定变换参数,就可以直接生成图像对中的第二张图像,以及光流场和occlusion map。然后我们将图像切成4份,就相当于扩展到4个图像对,每个图象的大小为$512 \times 384$。飞椅数据集的位移分布见Fig2右。
我们没有详细研究数据集参数对FlowNet性能的影响。但是我们发现,直接使用高斯分布对变换参数进行采样,训练出来的网络依然有效,但是不如上述采样策略得到的网络准确。
7.3.Convolutional Filters
当仔细观察FlowNet的filter时,我们发现网络低层的filter结构性更差,而网络高层的filter结构性更好。Fig3是网络第一层filter的可视化。应用于相关层输出的filter则具有非常明显的结构,见Fig5。对于不同大小和方向的光流选择不同的filter。

Fig3是FlowNetCorr第一层的filter。filter有很多噪音,但仍能看到一些结构。

Fig5是应用在FlowNetCorr相关层输出的filter的可视化。一共有256个filter,对于每个filter,我们用一个$21 \times 21$像素大小的patch来表示其权重,patch中的每个像素表示位移矢量。每个patch的中心表示0位移。每个filter都支持一种特定的运动模式。
filter可视化这里作者并没有提及可视化的方法。
7.4.Video
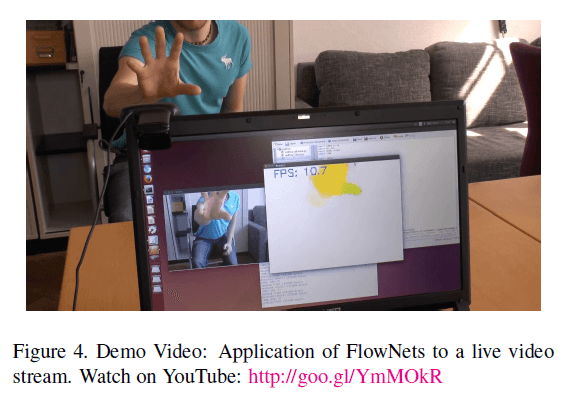
在补充视频中,我们使用带有GeForce GTX 980M GPU的笔记本电脑演示了FlowNet的实时操作。图像分辨率为$640 \times 480$。我们展示了FlowNetSimple和FlowNetCorr在室内和室外场景中的检测。视频放在了http://goo.gl/YmMOkR。示例可见Fig4。
8.原文链接
👽FlowNet:Learning Optical Flow with Convolutional Networks